Los Conjuntos Numéricos

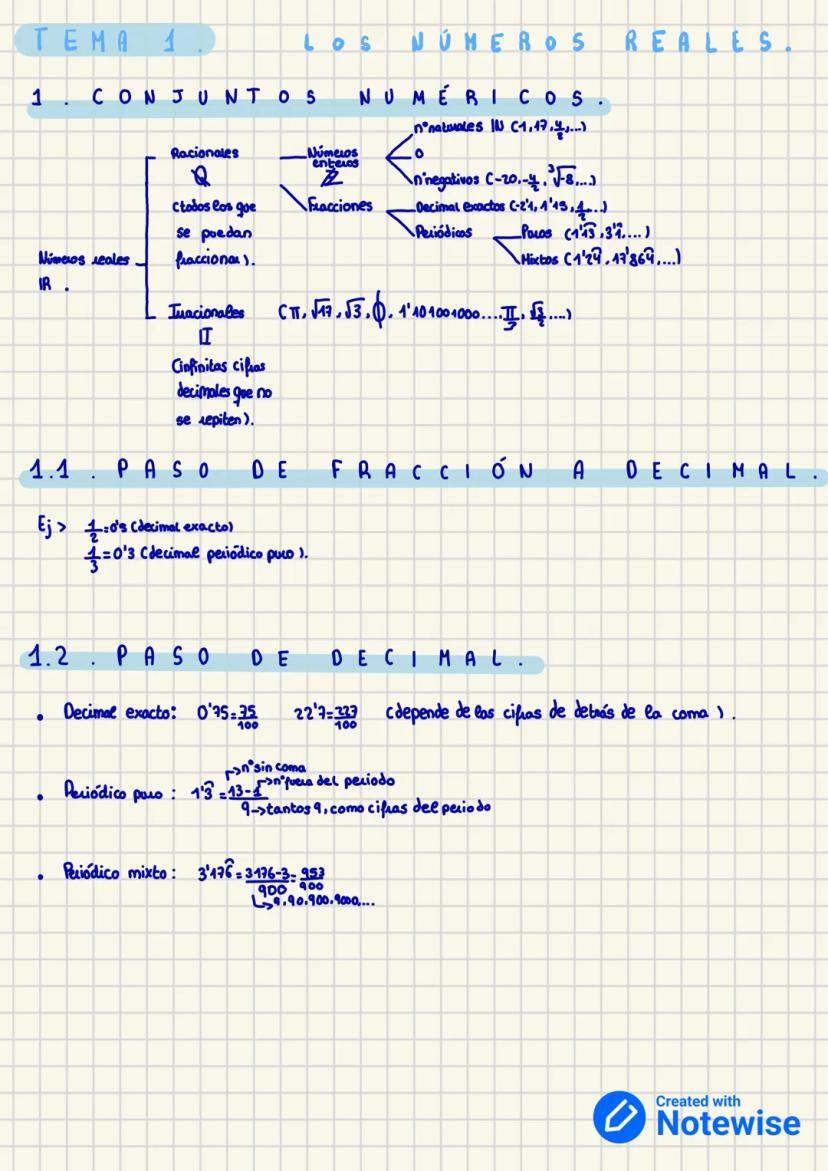
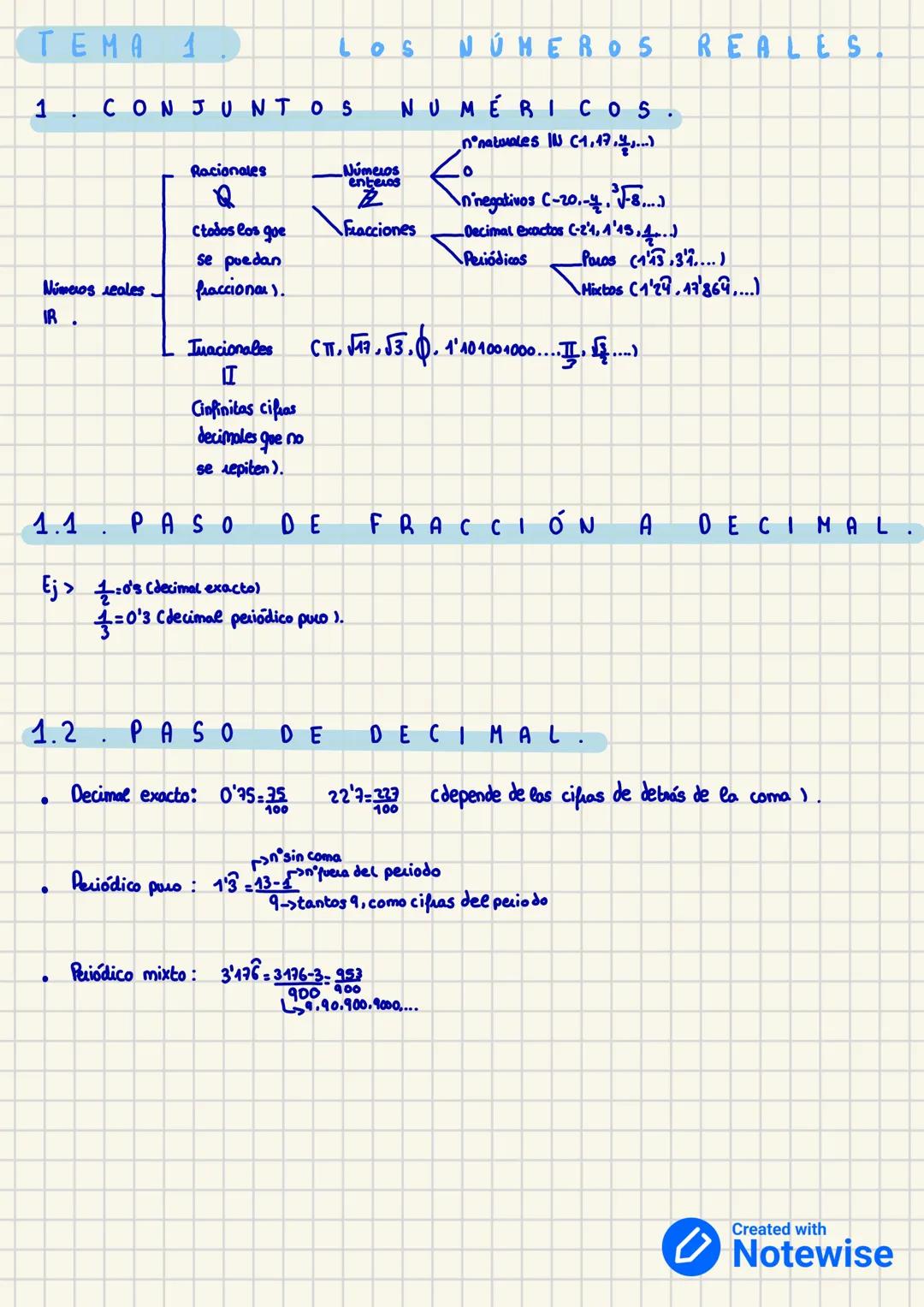
Imagínate los números como una gran familia con diferentes "personalidades". Los números naturales (ℕ) son los más básicos: 1, 2, 3... Los que usas para contar cosas. Cuando añades el cero y los negativos, obtienes los números enteros (ℤ).

Los números racionales (ℚ) incluyen todas las fracciones y decimales que se comportan bien. Pueden ser decimales exactos (como 0,25), periódicos puros (como 0,333...) o periódicos mixtos (como 1,2999...). Lo importante es que todos se pueden escribir como fracciones.

Los números irracionales (𝕀) son los "rebeldes" - como π o √2. Sus decimales nunca terminan ni se repiten. Juntos, racionales e irracionales forman los números reales (ℝ), que cubren toda la recta numérica.

Truco clave: Si puedes escribir un número como fracción, es racional. Si no, es irracional.

Conversiones Entre Fracciones y Decimales

Convertir entre fracciones y decimales es más fácil de lo que parece. Para pasar de decimal exacto a fracción, simplemente pon el número sin coma en el numerador y tantos ceros como cifras decimales haya en el denominador: 0,95 = 95/100.

Para los periódicos puros, como 1,333..., restas el número antes del periodo (13) menos el número sin periodo (1), y lo divides entre tantos 9 como cifras se repitan: (13-1)/9 = 12/9.

Los periódicos mixtos son un poco más complicados. Para 3,4999..., haces (3499-34)/900. El truco está en usar 9 para las cifras que se repiten y 0 para las que no.

Consejo: Practica con números sencillos primero. Una vez que pillez el patrón, será automático.

Intervalos y Notación Científica

Los intervalos te permiten describir rangos de números de forma precisa. Los paréntesis ( ) excluyen el número, mientras que los corchetes [ ] lo incluyen. Es como decidir si una puerta está abierta o cerrada en cada extremo.

La notación científica es tu mejor amiga para números súper grandes o súper pequeños. Un número como 2.300.000 se convierte en 2,3 × 10⁶. La mantisa (2,3) va entre 1 y 10, y el exponente (6) te dice cuántas posiciones mover la coma.

Para convertir a notación científica, mueve la coma hasta tener un solo dígito antes de ella. Cuenta las posiciones: hacia la izquierda da exponente positivo, hacia la derecha da negativo.

Los errores de aproximación se miden con error absoluto $|valor aproximado - valor real|$ y error relativo (error absoluto dividido entre valor real).

Dato útil: La notación científica es obligatoria en calculadoras para números muy grandes o pequeños.

Trabajando con Radicales

Los radicales son otra forma de escribir potencias con exponentes fraccionarios: ∛(a²) = a^(2/3). Esta conexión te permite usar las reglas de potencias para simplificar radicales complicados.

Para extraer factores, busca potencias perfectas dentro del radical. En ∛(81a⁴b³), puedes sacar 3 (de 3³) y b (de b³). Para introducir factores, eleva el número de fuera al índice del radical.

Cuando operes con radicales, necesitas el mismo índice. Para reducir a índice común, encuentra el mcm de los índices y ajusta los exponentes proporcionalmente.

Multiplicar y dividir radicales con el mismo índice es directo: ∛2 · ∛3 = ∛6. Para sumar y restar, los radicales deben ser equivalentes (como términos semejantes).

Estrategia: Siempre busca factores perfectos primero - hace todo más fácil.

Racionalización de Denominadores

La racionalización elimina radicales del denominador de una fracción. Es como "limpiar" la expresión para que se vea más presentable y sea más fácil de trabajar.

Para el Tipo 1 (un solo radical), multiplica numerador y denominador por el mismo radical: 4/√2 × √2/√2 = 4√2/2. Para el Tipo 2 (radicales cúbicos o superiores), completa la potencia del denominador.

El Tipo 3 es el más interesante: cuando tienes sumas o restas con radicales. Usas el conjugado (cambias el signo del medio) para crear una diferencia de cuadrados que elimine los radicales.

Estas técnicas no solo hacen que las expresiones se vean mejor, sino que facilitan cálculos posteriores y comparaciones entre números.

Recuerda: El conjugado de $√a + √b$ es $√a - √b$, y su producto elimina los radicales.

Logaritmos: La Operación Inversa

Los logaritmos son la operación inversa de las potencias. Si a^x = b, entonces log_a(b) = x. Es como preguntarse: "¿a qué potencia debo elevar a para obtener b?"

Los logaritmos especiales incluyen log_a(a) = 1 (cualquier número elevado a 1 es él mismo) y log_a(1) = 0 (cualquier número elevado a 0 es 1). El logaritmo neperiano (ln) usa la base e ≈ 2,718.

Las propiedades de logaritmos convierten multiplicaciones en sumas: log_a(A·B) = log_a(A) + log_a(B). Las divisiones se vuelven restas, y las potencias bajan como multiplicadores: log_a$A^n$ = n·log_a(A).

Estas propiedades son súper útiles para resolver ecuaciones exponenciales y simplificar expresiones complicadas.

Consejo: Los logaritmos transforman operaciones difíciles en operaciones fáciles.

Herramientas Algebraicas Esenciales

Las leyes de exponentes son tus herramientas básicas: a^m × a^n = a^$m+n$ para multiplicar, a^m ÷ a^n = a^$m-n$ para dividir, y $a^m$^n = a^(mn) para potencia de potencia. El exponente cero siempre da 1, y los exponentes negativos crean fracciones.

Los productos notables te ahorran tiempo en factorizaciones. $a+b$² = a² + 2ab + b², $a-b$² = a² - 2ab + b², y $a+b$$a-b$ = a² - b² son los más importantes. El binomio con término común $x+a$$x+b$ = x² + $a+b$x + ab aparece constantemente.

Para expresiones más complejas, tienes el cubo de binomio y el cuadrado de trinomio. Memorizar estos patrones te permite reconocer y factorizar expresiones rápidamente.

Práctica inteligente: Reconocer estos patrones al instante te convierte en un algebrista más eficiente.