Clasificación de los Números

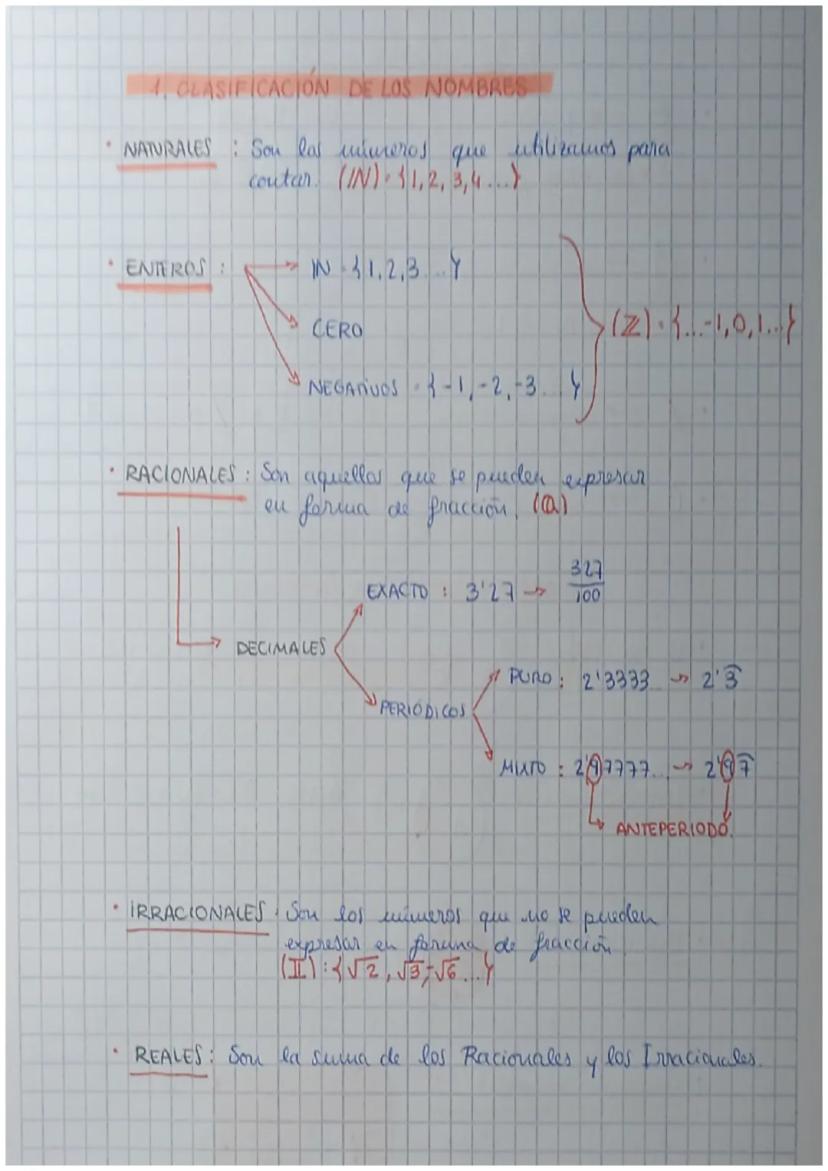
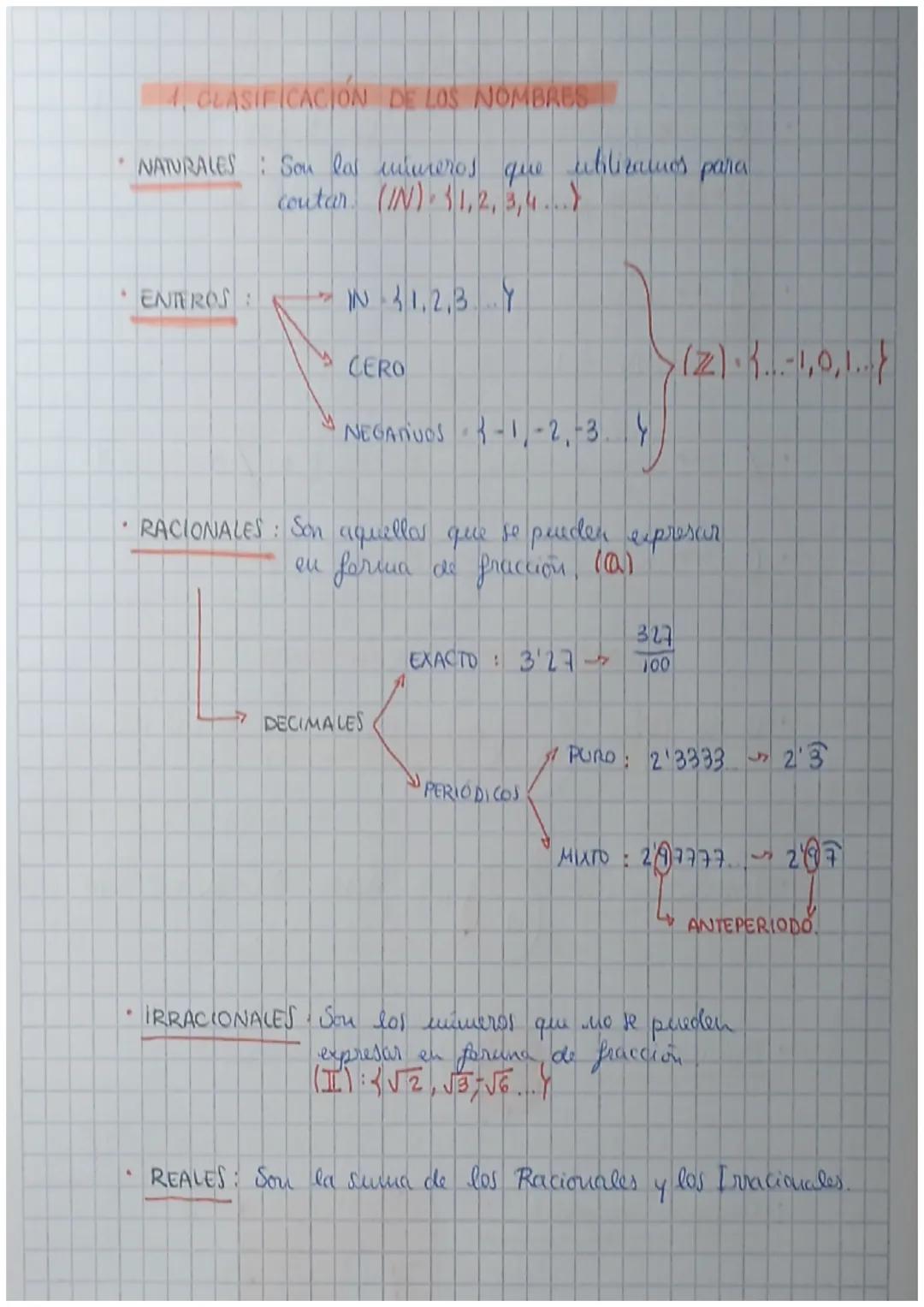
Los números naturales (ℕ) son los que usas para contar: 1, 2, 3, 4... Son los más básicos y los que conoces desde pequeño.

Los números enteros (ℤ) incluyen los naturales, el cero y los negativos: -3, -2, -1, 0, 1, 2, 3... Básicamente, todos los números sin decimales.

Los números racionales (ℚ) son los que puedes escribir como fracción. Por ejemplo, 3,27 = 327/100. También incluyen decimales periódicos como 2,333... donde el 3 se repite, o mixtos como 2,97777... donde solo el 7 se repite después del 9.

Los números irracionales no se pueden expresar como fracción, como π o √2. Los números reales son todos juntos: racionales + irracionales.

Truco: Si puedes escribirlo como fracción, es racional. Si no, es irracional.

Simbología y Operaciones con Conjuntos

El símbolo ∈ significa "pertenece a". Por ejemplo: 4 ∈ ℕ (el 4 pertenece a los naturales), pero -3 ∉ ℕ $el -3 NO pertenece a los naturales$.

Las operaciones con conjuntos más importantes son la unión (∪) que junta elementos, y la intersección (∩) que encuentra elementos comunes. Por ejemplo: ℝ = ℚ ∪ ℝ (los reales son la unión de racionales e irracionales).

Los símbolos lógicos ⟹ y ⟺ te ayudan a expresar relaciones. El primero significa "implica" (si una cosa, entonces otra), el segundo significa "equivale" (las dos afirmaciones son iguales).

Consejo: Practica estos símbolos porque los verás constantemente en matemáticas y te facilitarán mucho la vida.

Intervalos y Semirrectas

Los intervalos son rangos de números entre dos valores. Puedes escribirlos de varias formas: [1,6] significa desde 1 hasta 6 incluidos ambos, mientras que (1,6) significa desde 1 hasta 6 sin incluirlos.

La unión de intervalos (∪) combina rangos. Por ejemplo: [1,6] ∪ [2,5] = [1,6]. La intersección (∩) encuentra la parte común: [1,6] ∩ [2,7] = [2,6].

Para resolver estos ejercicios, dibuja una recta numérica y marca los intervalos. Así verás fácilmente qué números pertenecen a cada conjunto.

Dato útil: Los corchetes [ ] incluyen el número, los paréntesis ( ) lo excluyen. ¡No los confundas!

Propiedades de las Potencias

Multiplicar potencias de la misma base es súper fácil: sumas los exponentes. Por ejemplo: 2³ · 2⁵ = 2⁸. Para dividirlas, restas los exponentes: 3⁴ : 3¹ = 3³.

Con potencias del mismo exponente, puedes multiplicar las bases: 2⁵ · 3⁵ = 6⁵. Para dividir: 18³ : 9³ = 2³.

La potencia de una potencia multiplica los exponentes: (3²)⁵ = 3¹⁰. Y recuerda: cualquier número elevado a cero da 1.

Regla de oro: Cuando tengas dudas con potencias, descompón paso a paso y aplica una propiedad cada vez.

Raíces y Radicales

Una raíz es lo contrario de una potencia: ∜16 = ±4 porque 4² = 16 y (-4)² = 16. El número pequeño arriba es el índice, lo que está dentro es el radicando.

Con índice par y base positiva tienes dos soluciones (±). Con base negativa no hay solución en los reales. Con índice impar siempre hay una solución, sea la base positiva o negativa.

Por ejemplo: ∛8 = 2, √16 = ±4, ∛(-8) = -2, pero ∜(-16) no tiene solución real.

Truco para recordar: Par = problemático con negativos, impar = siempre funciona.

Operaciones con Radicales

Puedes escribir raíces como potencias fraccionarias: ⁿ√(aᵐ) = aᵐ/ⁿ. Esto te permite simplificar: ⁶√(3⁴) = ³√(3²).

Para sumar y restar radicales necesitas el mismo índice y radicando: 3⁷√5 + 2⁷√5 = 5⁷√5. Si no los tienes iguales, primero debes simplificar.

La extracción de factores saca del radical las potencias completas. Por ejemplo: ∛81 = 3∛3 porque 81 = 3³ · 3.

Estrategia: Siempre descompón en factores primos para ver qué puedes sacar del radical.

Operaciones Avanzadas con Radicales

Para multiplicar o dividir radicales necesitas el mismo índice. Si no lo tienes, busca el índice común (como el mínimo común múltiplo): √2 y ⁵√(3⁴) se convierten en ¹⁵√(2⁵) y ¹⁵√(3¹²).

Después ya puedes operar normalmente: ¹⁰√3 · ³√5 = ¹⁰⁶√(3³ · 5²).

La potencia de un radical es: (ᵠ√(aᵖ))ᵐ = ᵠ√(aᵖ·ᵐ). El radical de un radical es: ʳ√(ᵠ√(aᵖ)) = ʳ·ᵠ√(aᵖ).

Consejo: No te agobies con tantas reglas. Practica con ejemplos sencillos primero.

Más Operaciones con Radicales

Las operaciones con radicales siguen patrones lógicos. La potencia de un radical mantiene el índice pero multiplica el exponente del radicando.

El radical de un radical multiplica los índices: si tienes una raíz dentro de otra, multiplicas los números pequeños de arriba.

Estas reglas te permiten simplificar expresiones complejas paso a paso.

Importante: Siempre verifica tus resultados substituyendo valores sencillos.

Racionalización

La racionalización elimina radicales del denominador porque es más fácil trabajar así. Con un término, multiplicas arriba y abajo por el mismo radical: 3/√2 · √2/√2 = 3√2/2.

Con dos términos usas el conjugado (cambias el signo del medio): 5/(3-√2) · (3+√2)/(3+√2). Esto funciona porque $a-b$$a+b$ = a² - b².

El resultado es siempre una fracción sin radicales en el denominador.

Truco: El conjugado de $a - b$ es $a + b$, y viceversa. ¡Así de simple!

Logaritmos

Un logaritmo es lo contrario de una potencia: log_a b = c significa que aᶜ = b. La base no puede ser 1 ni menor que 1, y el argumento debe ser positivo.

Las propiedades principales son: log_a a = 1, log_a 1 = 0, log_a(b·c) = log_a b + log_a c, y log_a$b/c$ = log_a b - log_a c.

Para potencias: log_a(bⁿ) = n · log_a b. Para cambiar de base: log_a b = log_c b / log_c a.

Calculadora: Usa la fórmula de cambio de base para calcular cualquier logaritmo con tu calculadora.