Determinantes y Sistemas de Ecuaciones
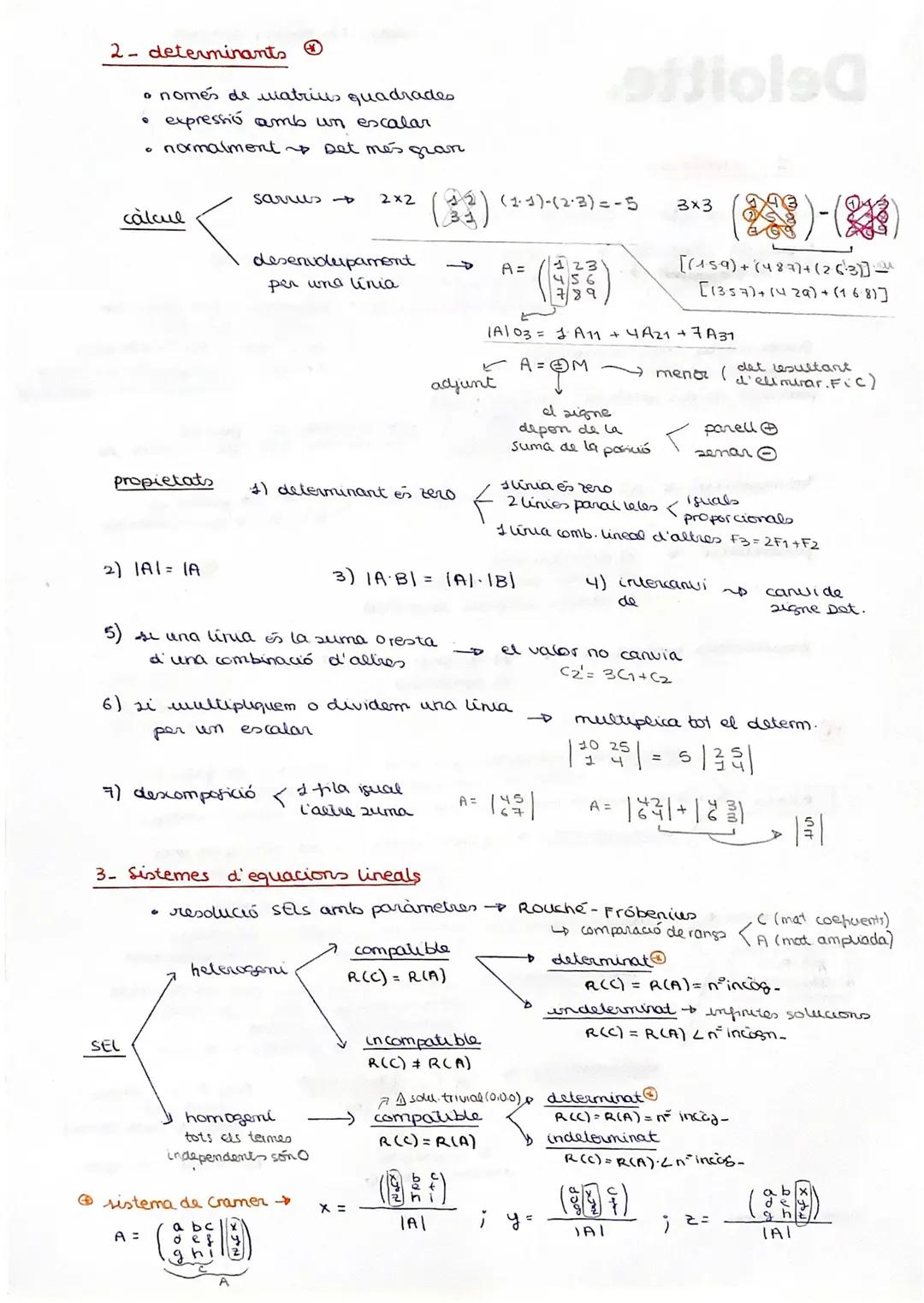
Los determinantes solo se calculan para matrices cuadradas y te dan un número escalar súper importante. Para matrices 2×2 es fácil: ad - bc. Para matrices 3×3, usa la regla de Sarrus o desarrolla por una fila/columna.
Las propiedades de los determinantes te facilitan mucho los cálculos. Si una fila es cero, el determinante es cero. Si intercambias dos filas, el determinante cambia de signo. Si multiplicas una fila por un escalar, el determinante se multiplica por ese escalar.
Los sistemas de ecuaciones lineales se clasifican según la relación entre los rangos de la matriz de coeficientes R(C) y la ampliada R(A). Si R(C) ≠ R(A), el sistema es incompatible (sin solución).
Regla de oro: Para sistemas compatibles, si R(C) = R(A) = número de incógnitas, tienes solución única. Si R(C) = R(A) < número de incógnitas, infinitas soluciones.
Los sistemas de Cramer son un caso especial donde puedes usar determinantes directamente para encontrar las soluciones: x = |Ax|/|A|, donde |Ax| es el determinante sustituyendo la columna x por los términos independientes.