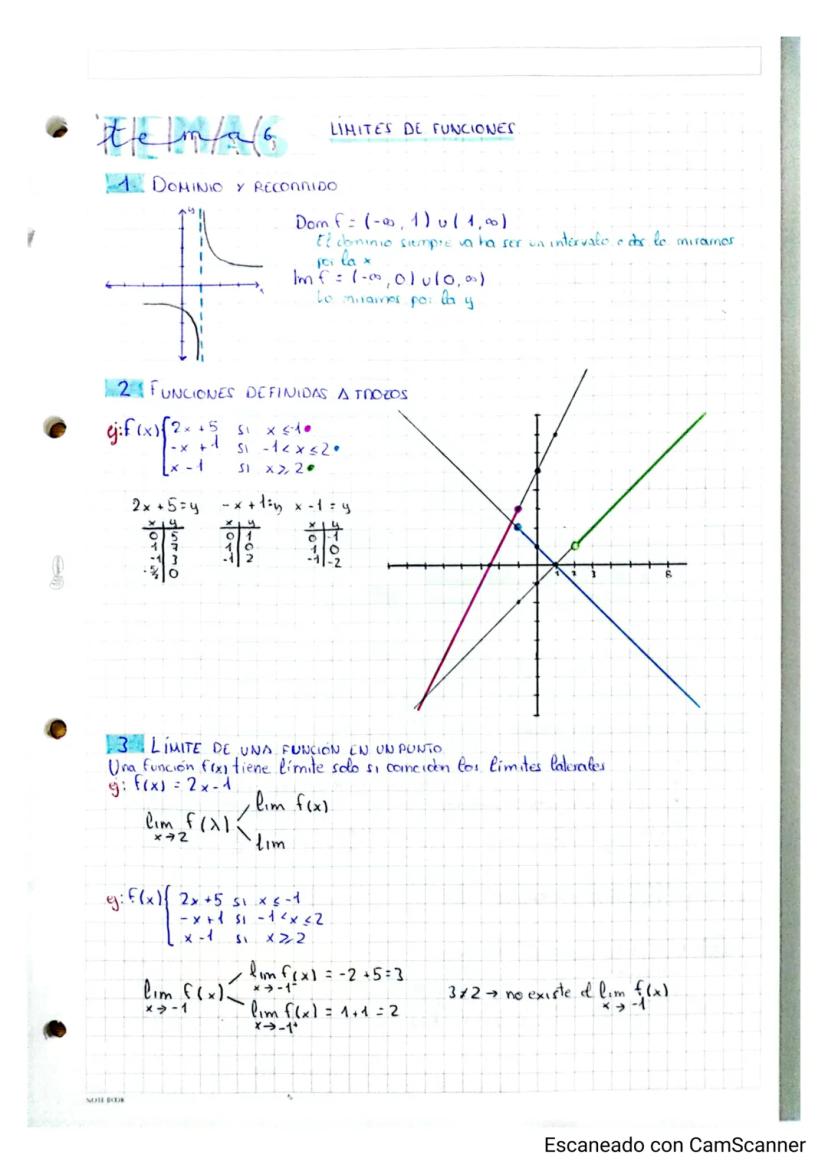
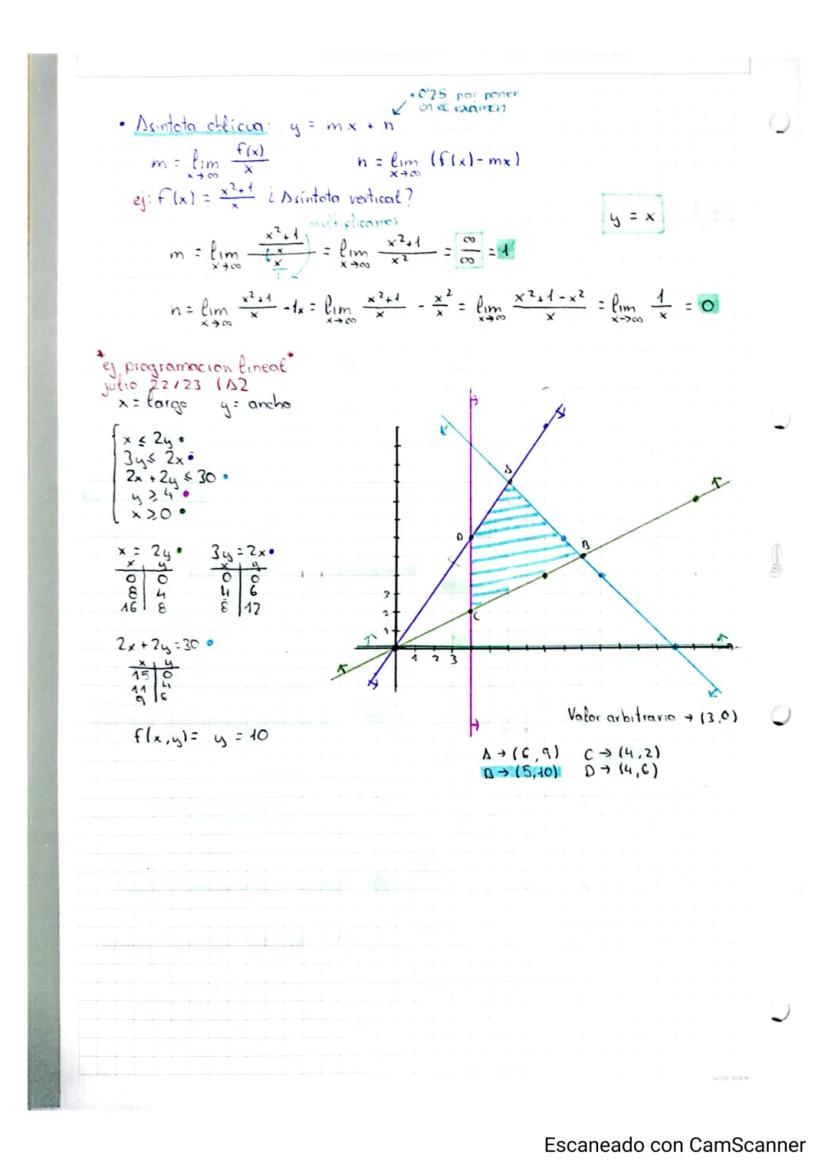
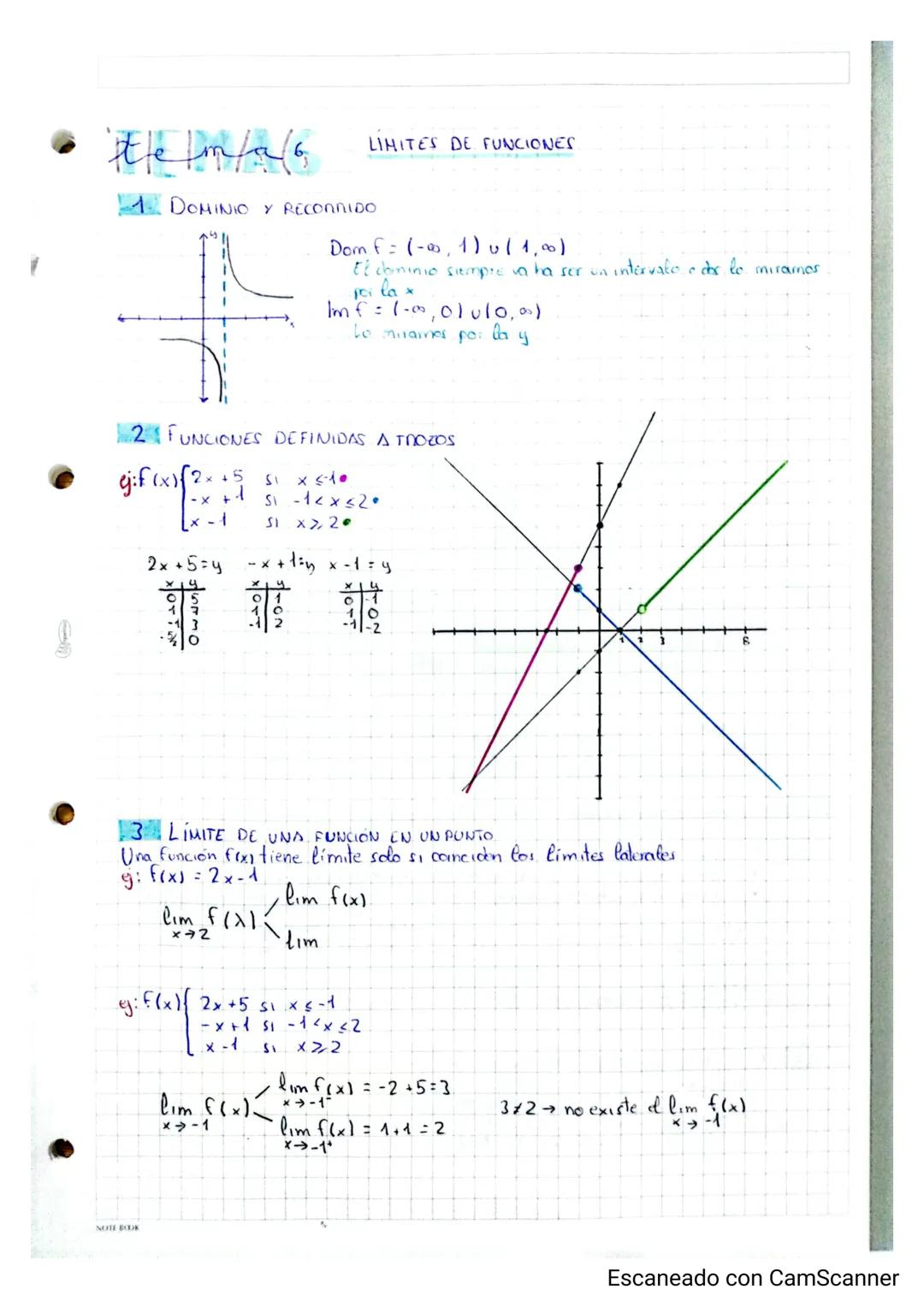
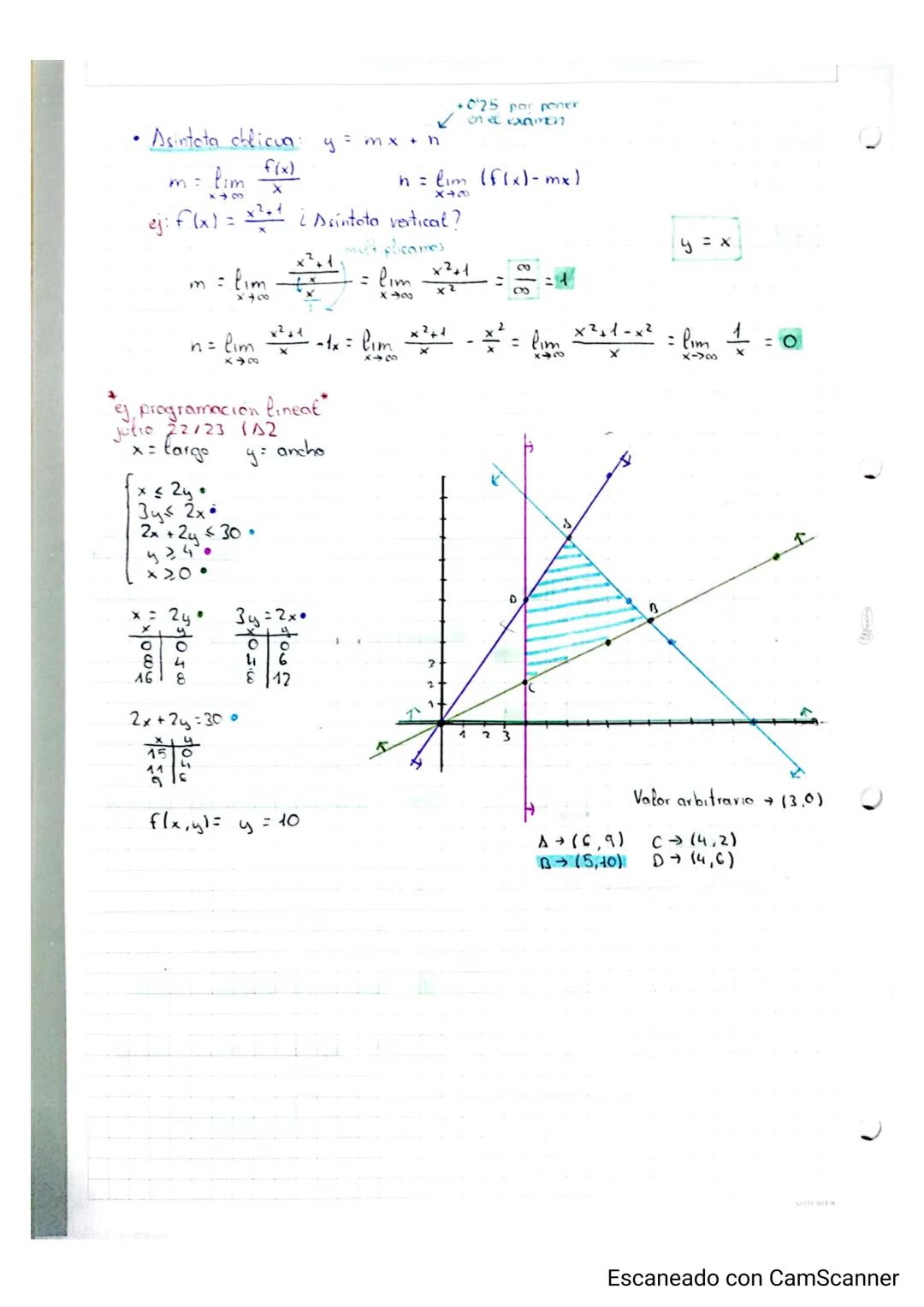
Límites que se van al Infinito
Cuando calculas límites y te sale algo como 4/0, no te asustes - significa que la función se va al infinito. Si el denominador se acerca a 0⁺ (por valores positivos), el límite será +∞ o -∞ según el signo del numerador.
Los límites en el infinito tienen sus propias reglas cuando te aparece ∞/∞ o 0/0 (indeterminaciones). Para resolverlos, compara los grados del numerador y denominador: si el grado del numerador es mayor, el límite es ∞; si son iguales, divide los coeficientes principales; si el denominador tiene mayor grado, el límite es 0.
Cuando te encuentres con 0/0, usa la regla de L'Hôpital: deriva numerador y denominador por separado y vuelve a calcular el límite. Es como tener un superpoder matemático para resolver indeterminaciones.
Consejo de examen: Si te sale 0/0 o ∞/∞, siempre intenta L'Hôpital primero - es el método más directo y rápido.