Fundamentos de la Trigonometría

¿Sabías que la trigonometría tiene sus raíces en el trabajo de Hipatía de Alejandría y Ptolomeo? Esta herramienta matemática transforma medidas angulares en medidas lineales, algo súper práctico para resolver problemas reales.

Las razones trigonométricas básicas (seno, coseno y tangente) se definen a partir de un triángulo rectángulo. Para un ángulo agudo α:

• sen α = cateto opuesto/hipotenusa
• cos α = cateto adyacente/hipotenusa
• tg α = cateto opuesto/cateto adyacente

Las relaciones fundamentales son tres fórmulas que siempre se cumplen y que te van a salvar en muchos ejercicios. La más importante es sen²α + cos²α = 1, que viene directamente del teorema de Pitágoras. También tienes tg α = sen α/cos α y 1 + tg²α = 1/cos²α.

Truco clave: Si conoces una razón trigonométrica, puedes calcular las otras dos usando estas relaciones fundamentales.

La Circunferencia Trigonométrica

Cuando trabajamos con ángulos de 0° a 360°, utilizamos la circunferencia trigonométrica de radio 1 centrada en el origen. Aquí cada punto se representa como (cos α, sen α), lo que hace todo mucho más visual.

Los signos de las razones trigonométricas cambian según el cuadrante:

• Cuadrante I (0°-90°): todas positivas
• Cuadrante II (90°-180°): solo seno positivo
• Cuadrante III (180°-270°): solo tangente positiva
• Cuadrante IV (270°-360°): solo coseno positivo

Para ángulos mayores de 360° o negativos, recuerda que α y α ± 360°k (donde k es entero) tienen las mismas razones trigonométricas. Es como dar vueltas completas a la circunferencia.

Dato importante: La tangente de 90° y 270° es infinito porque el coseno vale cero en esos ángulos.

Relaciones Especiales y Resolución de Triángulos

Hay tres tipos de relaciones angulares que simplifican muchísimo los cálculos. Los ángulos complementarios $α y 90°-α$ cumplen que sen(90°-α) = cos α. Los ángulos suplementarios $α y 180°-α$ tienen sen(180°-α) = sen α pero cos(180°-α) = -cos α. Los ángulos opuestos (-α) mantienen el coseno pero cambian el signo del seno.

Para resolver triángulos rectángulos, tienes dos casos principales. Si conoces dos lados, usas Pitágoras para el tercero y las razones trigonométricas para los ángulos. Si conoces un lado y un ángulo, las razones trigonométricas te dan los otros lados.

El área de cualquier triángulo se puede calcular con A = (a·b·sen α)/2, donde α es el ángulo entre los lados a y b. También puedes usar la fórmula de Herón si conoces los tres lados.

Aplicación práctica: Estos conceptos son fundamentales para topografía, navegación y cualquier problema que involucre distancias y alturas.

Teorema del Seno

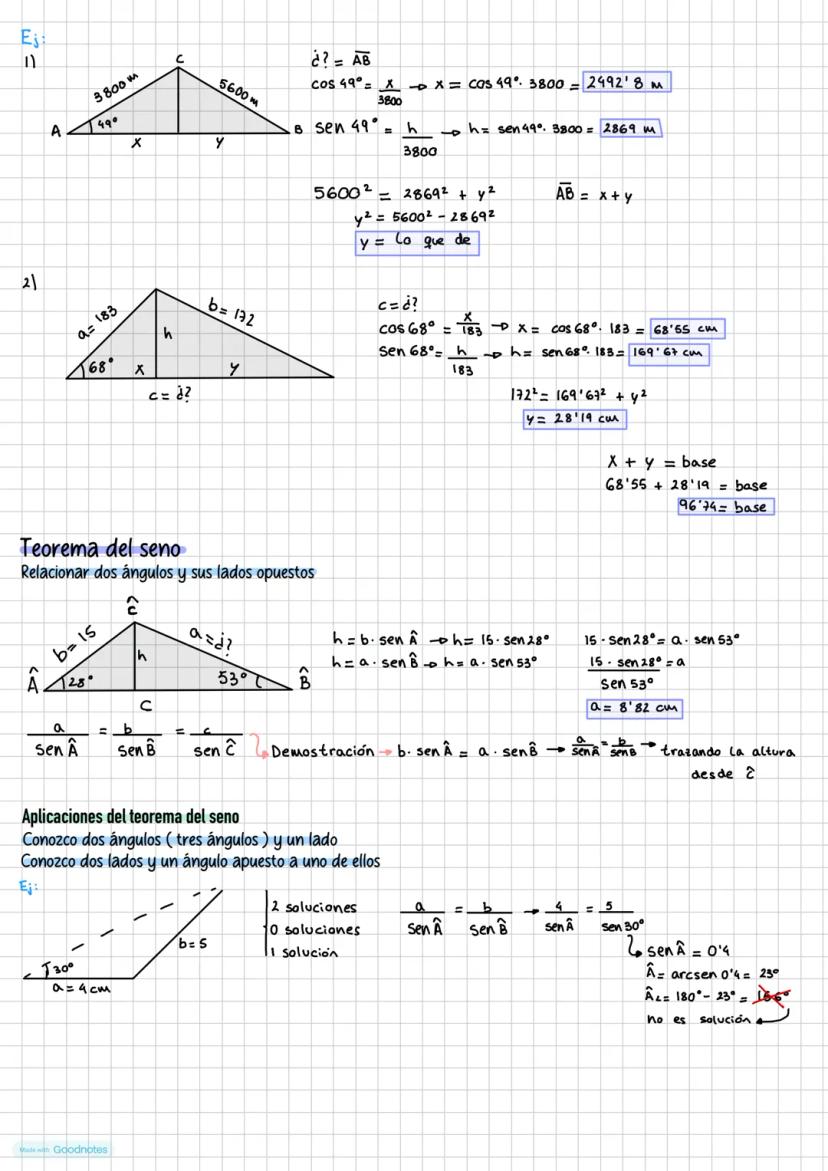
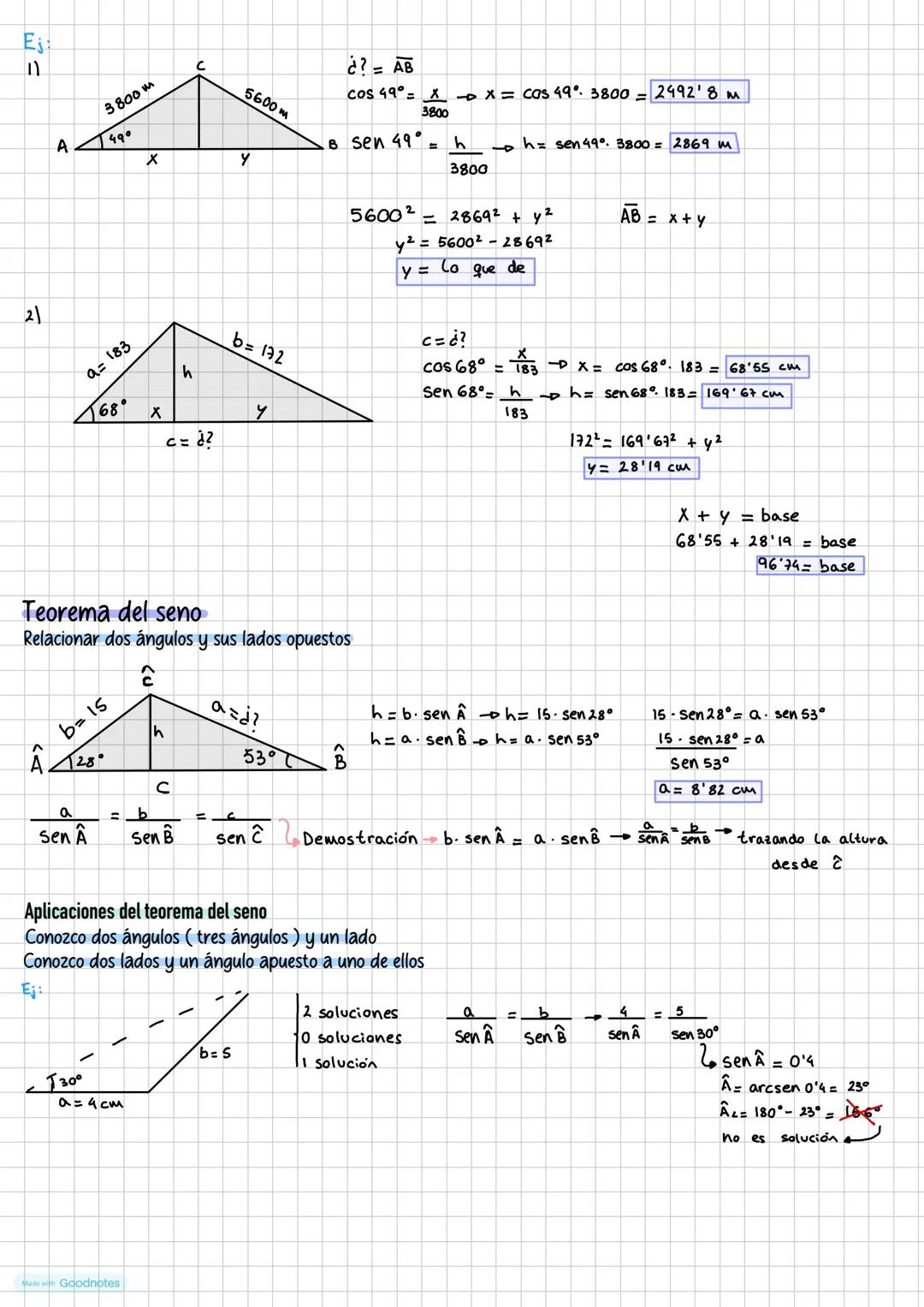
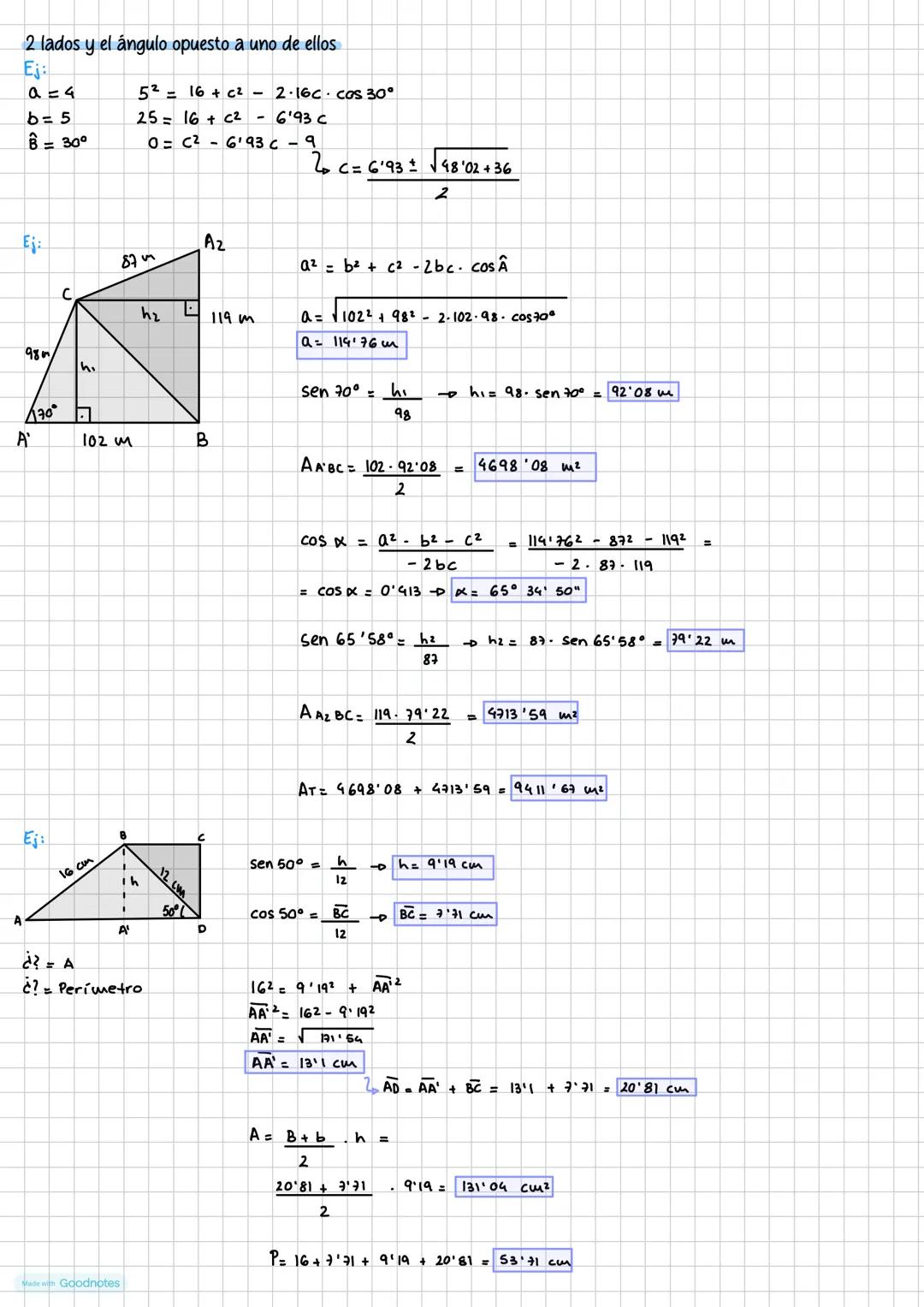
El teorema del seno es tu mejor aliado cuando trabajas con triángulos que no son rectángulos. La fórmula clave es a/sen  = b/sen B̂ = c/sen Ĉ, que relaciona cada lado con el seno de su ángulo opuesto.

Este teorema se aplica en dos situaciones específicas: cuando conoces dos ángulos y un lado, o cuando conoces dos lados y un ángulo opuesto a uno de ellos. En el segundo caso, ten cuidado porque a veces puedes obtener dos soluciones, una solución o ninguna.

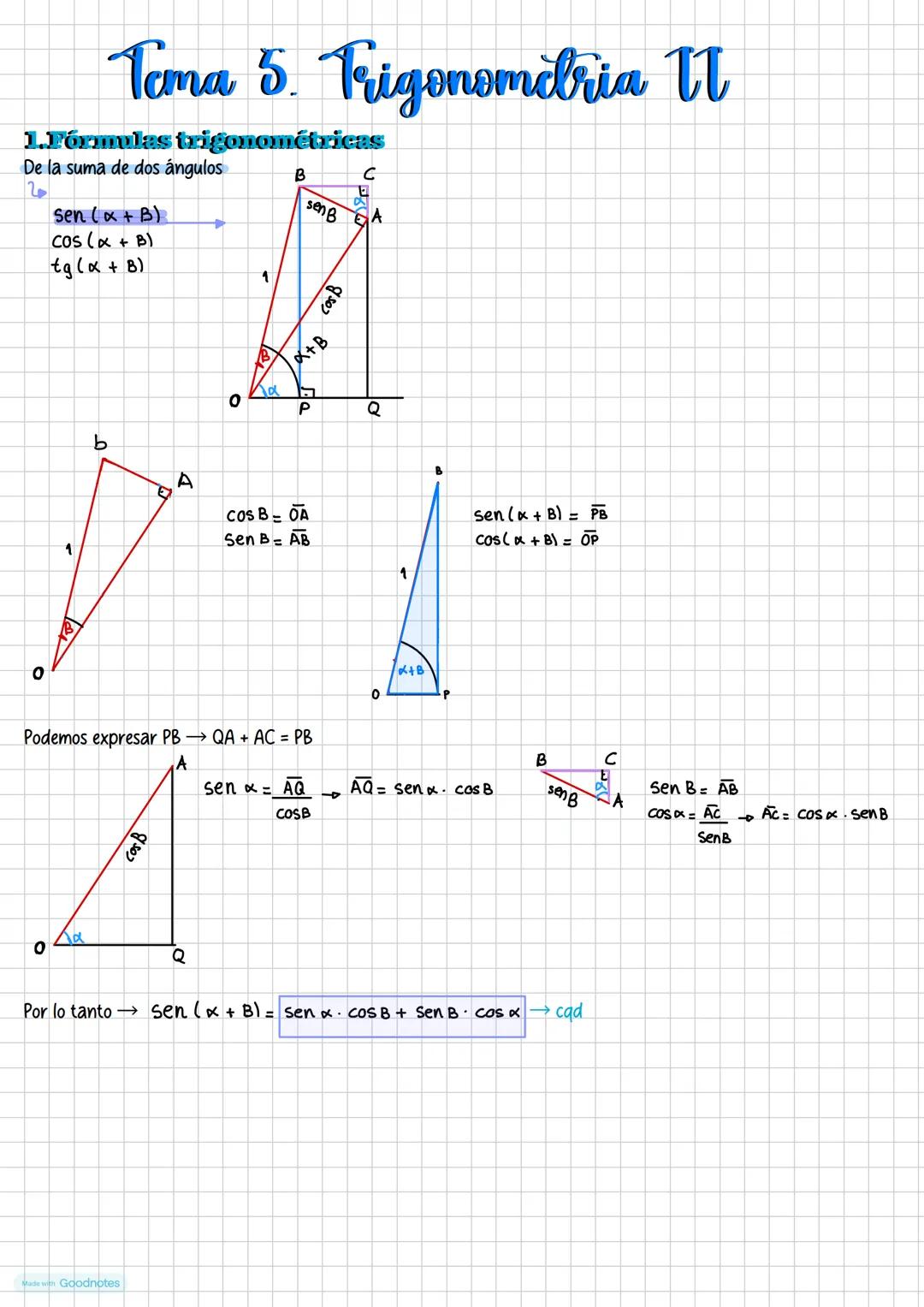
La demostración es bastante elegante y se basa en la altura del triángulo. Si trazas una altura h desde un vértice, puedes expresarla de dos formas diferentes usando el seno, y al igualar ambas expresiones obtienes el teorema.

Atención: En problemas con dos lados y un ángulo opuesto, siempre verifica si existen una o dos soluciones válidas.

Teorema del Coseno

El teorema del coseno es como una versión generalizada del teorema de Pitágoras que funciona para cualquier triángulo. La fórmula fundamental es a² = b² + c² - 2bc·cos Â.

Se usa principalmente en dos casos: cuando conoces los tres lados y quieres encontrar un ángulo, o cuando conoces dos lados y el ángulo que forman para encontrar el tercer lado. Es especialmente útil para triángulos que no tienen ángulos rectos.

La demostración utiliza coordenadas y el teorema de Pitágoras aplicado inteligentemente. Al proyectar uno de los lados sobre otro, aparece naturalmente el término con el coseno que hace que la fórmula funcione para cualquier tipo de triángulo.

Ventaja clave: Este teorema te permite resolver triángulos cuando el teorema del seno no se puede aplicar directamente.

Aplicaciones Avanzadas y Problemas Complejos

Cuando te enfrentas a figuras irregulares, la clave es descomponerlas en triángulos que puedas resolver. Utiliza alturas para crear triángulos rectángulos y luego aplica los teoremas del seno y coseno según corresponda.

Para calcular áreas totales, suma las áreas de los triángulos individuales. Recuerda que puedes usar A = (b·h)/2 para triángulos rectángulos o A = (a·b·sen α)/2 para cualquier triángulo.

Los perímetros se calculan sumando todos los lados externos de la figura. A veces necesitarás encontrar algunos lados usando trigonometría antes de poder calcular el perímetro total.

Estrategia ganadora: Dibuja siempre la figura, marca todos los datos conocidos y planifica qué triángulos vas a resolver primero.

Fórmulas Trigonométricas Avanzadas

Las fórmulas de suma y diferencia te permiten calcular razones trigonométricas de ángulos complejos. Las más importantes son:

• sen(α + β) = sen α·cos β + cos α·sen β
• cos(α + β) = cos α·cos β - sen α·sen β
• tg(α + β) = $tg α + tg β$/$1 - tg α·tg β$

La demostración geométrica usando la circunferencia trigonométrica es bastante elegante. Se basa en descomponer las proyecciones de un ángulo suma en términos de las razones trigonométricas de los ángulos individuales.

Tip de estudio: Una vez que dominas la fórmula del seno de la suma, puedes deducir todas las demás usando identidades trigonométricas básicas.

Ángulos Dobles y Mitades

Las fórmulas del ángulo doble son casos especiales de las fórmulas de suma cuando α = β:

• sen 2α = 2·sen α·cos α
• cos 2α = cos²α - sen²α
• tg 2α = 2tg α/$1 - tg²α$

Para ángulos mitad, las fórmulas involucran raíces cuadradas y el signo depende del cuadrante:

• sen(α/2) = ±√$(1-cos α)/2$
• cos(α/2) = ±√$(1+cos α)/2$

Estas fórmulas son fundamentales para simplificar expresiones complejas y resolver identidades trigonométricas. La clave está en reconocer cuándo aplicar cada una.

Método eficaz: Para verificar identidades, trabaja con el lado más complicado hasta llegar al más simple.

Identidades y Simplificaciones

Demostrar identidades trigonométricas requiere práctica y conocer bien las fórmulas básicas. La estrategia general es transformar el lado más complejo usando las fórmulas conocidas hasta llegar al lado más simple.

Las transformaciones más útiles incluyen:

• Sustituir sen 2x por 2·sen x·cos x
• Usar la identidad fundamental sen²x + cos²x = 1
• Aplicar fórmulas de ángulo doble y mitad cuando aparezcan

Cuando trabajas con fracciones trigonométricas, busca factores comunes y simplifica paso a paso. Muchas veces puedes factorizar expresiones usando las identidades básicas.

Consejo práctico: Si una demostración se complica mucho, prueba empezar desde el otro lado o usar una identidad diferente.

Ecuaciones Trigonométricas

Las ecuaciones trigonométricas tienen la incógnita en el ángulo y normalmente ofrecen múltiples soluciones. El procedimiento es encontrar las soluciones en el intervalo [0°, 360°) y luego generar todas las demás sumando k·360°.

Para resolver estas ecuaciones, transforma la expresión usando identidades hasta obtener una ecuación simple del tipo sen x = a, cos x = b o tg x = c. Luego usa las funciones inversas para encontrar los ángulos.

Siempre verifica tus soluciones sustituyéndolas en la ecuación original. Algunas transformaciones pueden introducir soluciones falsas que no satisfacen la ecuación inicial.

Estrategia clave: Si la ecuación tiene funciones trigonométricas diferentes, intenta expresar todo en términos de una sola función usando identidades.