Fundamentos Matemáticos y Jerarquía

Las matemáticas están llenas de símbolos y operaciones complejas, desde derivadas hasta integrales y matrices. Pero todo se basa en un principio fundamental: el orden importa.

La jerarquía de operaciones es la regla universal que establece qué operación hacer primero cuando tienes varias en una misma expresión. Sin esta regla, cada persona podría resolver la misma operación de forma diferente y obtener resultados distintos.

💡 Dato curioso: Sin la jerarquía de operaciones, la expresión 2 + 3 × 4 podría dar tanto 20 como 14. ¡Por eso necesitamos reglas claras!

Esta regla asegura que matemáticos de todo el mundo obtengan siempre el mismo resultado al resolver la misma expresión.

¿Qué es la Jerarquía de Operaciones?

La jerarquía de operaciones es tu hoja de ruta para resolver cualquier problema matemático sin confundirte. Piénsalo como las reglas de tráfico: todos las siguen para que el sistema funcione.

Esta regla establece el orden específico en el que debes realizar las operaciones matemáticas cuando aparecen varias juntas en una expresión. No es opcional ni depende de tu preferencia.

⚠️ Importante: Ignorar la jerarquía de operaciones es la causa número uno de errores en matemáticas. ¡Domínala y verás cómo mejoran tus notas!

Su propósito es simple pero crucial: garantizar que siempre obtengas el resultado correcto y que este resultado sea el mismo sin importar quién haga la operación.

¿Para Qué Sirve la Jerarquía?

Imagínate si cada vez que resolvieras 2 + 3 × 4 pudieras elegir si hacer primero la suma o la multiplicación. ¡Sería un caos total! La jerarquía evita precisamente esta confusión.

La jerarquía de operaciones asegura que las operaciones se realicen en el orden correcto para obtener siempre el resultado esperado. Es como tener un GPS matemático que te guía paso a paso.

🎯 Consejo: Piensa en la jerarquía como una receta de cocina. Si cambias el orden de los pasos, el resultado final será completamente diferente.

Gracias a esta regla, todos los matemáticos del mundo pueden comunicarse usando el mismo "idioma" y estar seguros de que sus cálculos son correctos.

El Orden Correcto de las Operaciones

Aquí tienes la secuencia exacta que debes seguir siempre, sin excepciones:

1. Grupos - Todo lo que esté dentro de paréntesis, corchetes o llaves va primero. 2. Exponentes - Potencias, raíces y logaritmos van en segundo lugar. 3. Multiplicación y División - Se resuelven de izquierda a derecha. 4. Adición y Sustracción - Van al final, también de izquierda a derecha.

📝 Truco de memoria: Recuerda "PEMDAS" en inglés o "GEMDAS" en español: Grupos, Exponentes, Multiplicación/División, Adición/Sustracción.

Esta secuencia es universal y nunca cambia, sin importar lo complicada que parezca la expresión matemática.

Grupos: Lo Primero es lo Primero

Los grupos son tu punto de partida obligatorio. Todo lo que esté encerrado en símbolos de agrupación debe resolverse antes que cualquier otra cosa.

En el ejemplo 2 × (3 + 1), primero resuelves lo que está dentro del paréntesis: (3 + 1) = 4. Luego haces la multiplicación: 2 × 4 = 8.

💡 Error común: Muchos estudiantes olvidan resolver primero los paréntesis y hacen 2 × 3 + 1 = 7. ¡Ese resultado está mal!

Si ignoras esta regla y haces las operaciones en otro orden, tu resultado será completamente incorrecto. Los grupos siempre tienen prioridad absoluta.

Símbolos de Agrupación

Existen varios tipos de símbolos de agrupación, y todos tienen el mismo poder: forzarte a resolver primero lo que contienen.

Los más comunes son paréntesis (), corchetes [] y llaves {}. Cuando aparecen anidados, resuelves desde el más interno hacia afuera.

En el ejemplo 5 × {3 + [2 × (3 + 1)]}, empiezas por (3 + 1) = 4, luego [2 × 4] = 8, después {3 + 8} = 11, y finalmente 5 × 11 = 55.

🔥 Tip pro: Cuando veas grupos anidados, trabaja como si estuvieras pelando una cebolla: capa por capa, desde adentro hacia afuera.

Más Símbolos de Agrupación

Los números mixtos y las barras de fracción también funcionan como símbolos de agrupación, aunque no lo parezcan a primera vista.

Un número mixto como 3⁴⁄₅ significa 3 + (4 ÷ 5). Primero resuelves la fracción y luego la sumas al número entero.

Las barras de fracción actúan como paréntesis invisibles. En ²⁺²⁄₅, primero sumas 2 + 2 = 4, y luego divides entre 5 para obtener ⁴⁄₅.

⚡ Atención: Las barras de fracción son símbolos de agrupación disfrazados. Siempre resuelve completamente el numerador y el denominador antes de hacer la división.

Funciones como Grupos

Las funciones son conjuntos de operaciones que tienen nombre propio y actúan como símbolos de agrupación súper especiales.

Funciones como sin(x), cos(x), tan(x), f(x) y g(x) deben resolverse completamente antes de continuar con otras operaciones. Son como cajas negras que procesan lo que contienen.

Si tienes 2 × sin(30°), primero calculas sin(30°) = 0.5, y luego haces la multiplicación: 2 × 0.5 = 1.

🎯 Recuerda: Las funciones siempre se resuelven antes que las operaciones que las rodean. Piénsalas como paréntesis con superpoderes.

Exponentes: El Segundo Escalón

Los exponentes ocupan el segundo lugar en la jerarquía y incluyen potencias, raíces y logaritmos. Son operaciones poderosas que pueden cambiar completamente el valor de una expresión.

Una potencia como 2³ significa 2 × 2 × 2 = 8. Siempre resuelves los exponentes antes que las multiplicaciones, divisiones, sumas o restas que los rodean.

Los exponentes tienen una característica especial: para "deshacerlos" necesitas dos operaciones diferentes (raíces y logaritmos), no solo una operación inversa.

⚠️ Importante: Los exponentes son más poderosos que la multiplicación. En 2 × 3², primero haces 3² = 9, luego 2 × 9 = 18.

Raíces y Logaritmos

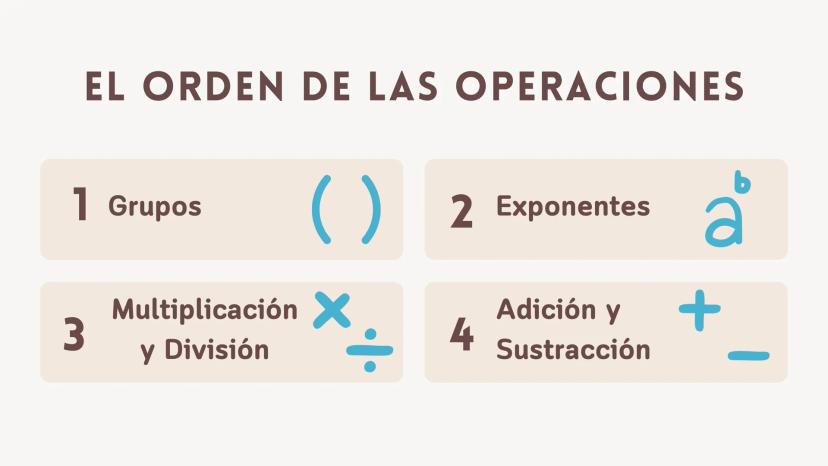
Las raíces (√x) y los logaritmos $log_a x$ también pertenecen al nivel de los exponentes en la jerarquía de operaciones.

Las raíces te ayudan a encontrar las posibles bases de una potencia. Por ejemplo, √9 = 3 porque 3² = 9.

Los logaritmos te ayudan a encontrar el exponente de una potencia. Por ejemplo, log₂ 8 = 3 porque 2³ = 8.

🚀 Consejo avanzado: Raíces y logaritmos son las "operaciones inversas" de los exponentes, pero en la jerarquía tienen el mismo nivel de prioridad.

Estas operaciones se resuelven al mismo tiempo que las potencias, antes que cualquier multiplicación, división, suma o resta.