Rectas Tangente y Normal: Las Básicas que Necesitas Dominar
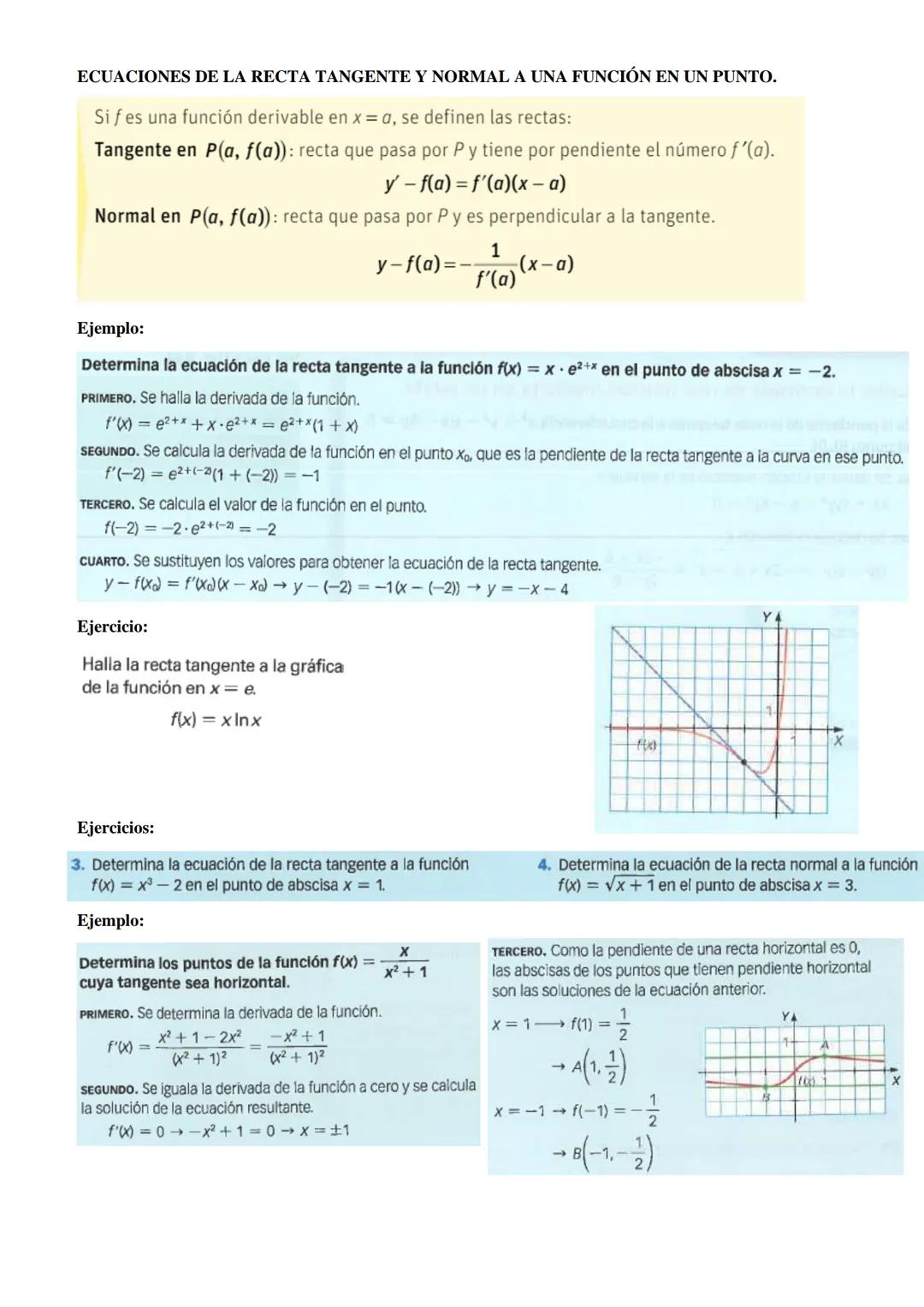
La recta tangente es esa línea que toca la curva en un punto sin cortarla, mientras que la recta normal es perpendicular a la tangente en ese mismo punto. Ambas pasan por el punto P(a, f) de la función.
Para la tangente, usas la fórmula: y - f = f'a$$x - a, donde f' es la pendiente. Para la normal, cambias la pendiente por su inverso negativo: y - f = -1/f'a$$x - a.
El proceso siempre sigue estos pasos: deriva la función, calcula f', encuentra f, y sustituye en la ecuación. Por ejemplo, con f = x·e^ en x = -2, obtienes f' = e^2+x$$1+x, luego f' = -1 y f = -2, dando la tangente y = -x - 4.
Truco clave: Las rectas horizontales tienen pendiente 0, así que para encontrarlas, iguala f' = 0 y resuelve.