Operaciones con polinomios y factorización

¿Sabías que los polinomios funcionan como números gigantes? Puedes sumarlos, restarlos, multiplicarlos y dividirlos siguiendo reglas específicas. La suma y resta son directas: solo combinas términos semejantes.

Para la división, tienes dos opciones geniales. La división tradicional te da cociente y resto, mientras que la regla de Ruffini es tu mejor amiga cuando divides por binomios del tipo $x + a$. Ruffini es mucho más rápida y menos propensa a errores.

La factorización es como descomponer un número en sus factores primos, pero con polinomios. Primero buscas las raíces (valores que hacen el polinomio igual a cero). Si los coeficientes son enteros, las raíces enteras siempre son divisores del término independiente.

Truco clave: El teorema del factor dice que si 'a' es raíz, entonces $x-a$ es un factor. ¡Esto te ahorra muchísimo tiempo!

Estrategias para encontrar raíces

Encontrar raíces es como ser detective matemático. Tienes pistas claras para seguir. Para raíces racionales, usa la regla: deben ser de la forma a/b, donde 'a' divide al término independiente y 'b' al coeficiente principal.

El método de Ruffini es tu herramienta estrella aquí. Cada vez que encuentres una raíz, úsalo para factorizar y reduce el grado del polinomio. Es como pelar una cebolla, capa por capa.

Tu estrategia ganadora: primero prueba las raíces enteras más simples (±1, ±2...). Si no funcionan, ve a por las racionales. Cuando el polinomio se reduzca a grado 2, usa la fórmula cuadrática.

Recuerda que no todos los polinomios tienen raíces reales. Si llegas a una ecuación de segundo grado sin solución real, ahí termina tu factorización.

Consejo pro: Siempre verifica tus raíces sustituyendo en el polinomio original. Un pequeño error de cálculo puede arruinar todo el proceso.

Ecuaciones polinómicas, bicuadradas y racionales

Las ecuaciones polinómicas son simplemente polinomios igualados a cero. Ya sabes resolverlas: factoriza y encuentra las raíces. Cada factor lineal te da una solución.

Las ecuaciones bicuadradas $tipo ax⁴ + bx² + c = 0$ tienen un truco genial: el cambio de variable z = x². Conviertes una ecuación de cuarto grado en una de segundo grado súper fácil de resolver.

Para las ecuaciones racionales, tu estrategia es eliminar fracciones. Encuentra el denominador común y multiplica toda la ecuación por él. Así transformas la ecuación en una polinómica normal.

Un detalle importante: después de resolver ecuaciones racionales, siempre verifica que las soluciones no anulen ningún denominador original. Si lo hacen, no son válidas.

Atención: En ecuaciones racionales, algunas soluciones pueden ser "fantasma". Siempre comprueba sustituyendo en la ecuación original.

Ecuaciones con radicales, logarítmicas y exponenciales

Las ecuaciones con radicales requieren paciencia. Aísla el radical y eleva al cuadrado para eliminarlo. Pero cuidado: este proceso puede crear soluciones falsas, así que siempre verifica al final.

En las ecuaciones logarítmicas, usa las propiedades de los logaritmos para simplificar. Si tienes log A = log B, entonces A = B. Es así de simple. Pero recuerda que solo puedes calcular logaritmos de números positivos.

Las ecuaciones exponenciales no tienen método único, pero tienes tres técnicas potentes: tomar logaritmos, igualar exponentes (cuando las bases son iguales), o hacer cambios de variable inteligentes.

El cambio de variable es especialmente útil cuando ves patrones repetitivos. Por ejemplo, si aparece 2^x varias veces, hazlo z = 2^x y resuelve la ecuación resultante.

Verificación crucial: En radicales y logarítmicas, siempre comprueba las soluciones. Pueden aparecer valores que no tienen sentido matemático.

Sistemas de ecuaciones lineales y no lineales

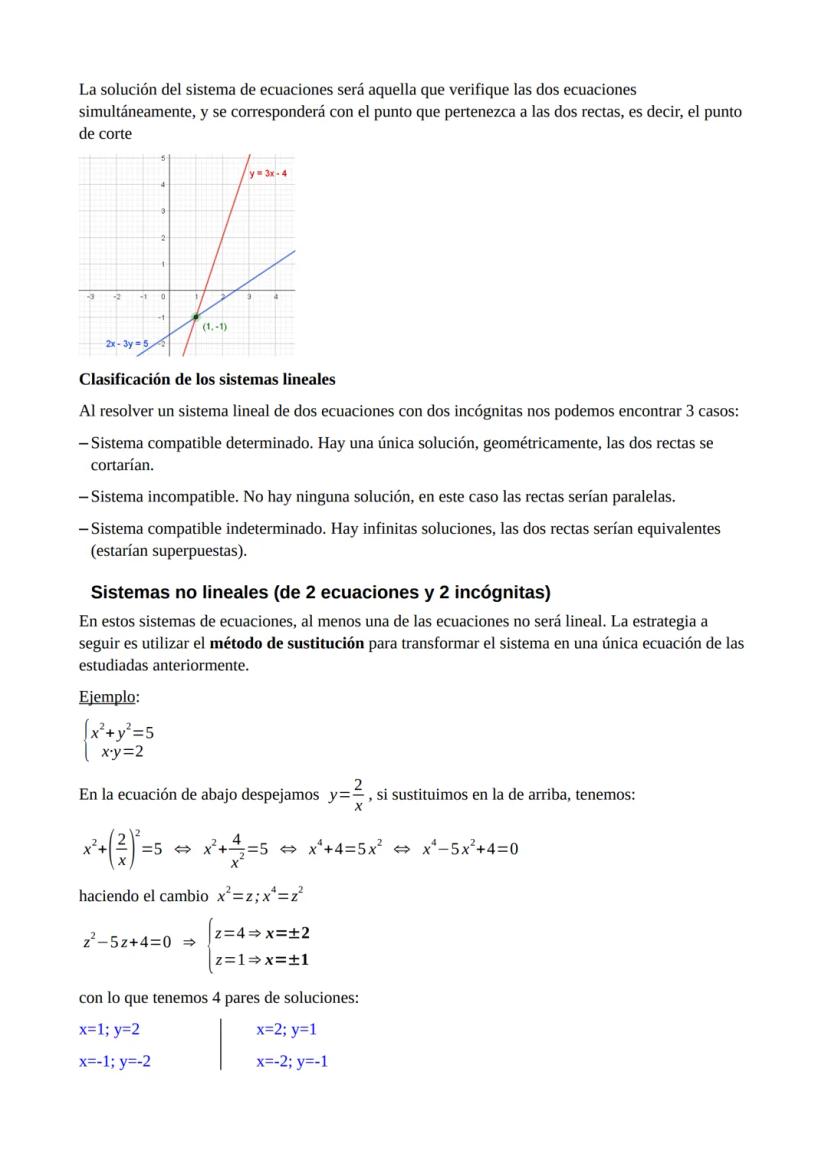
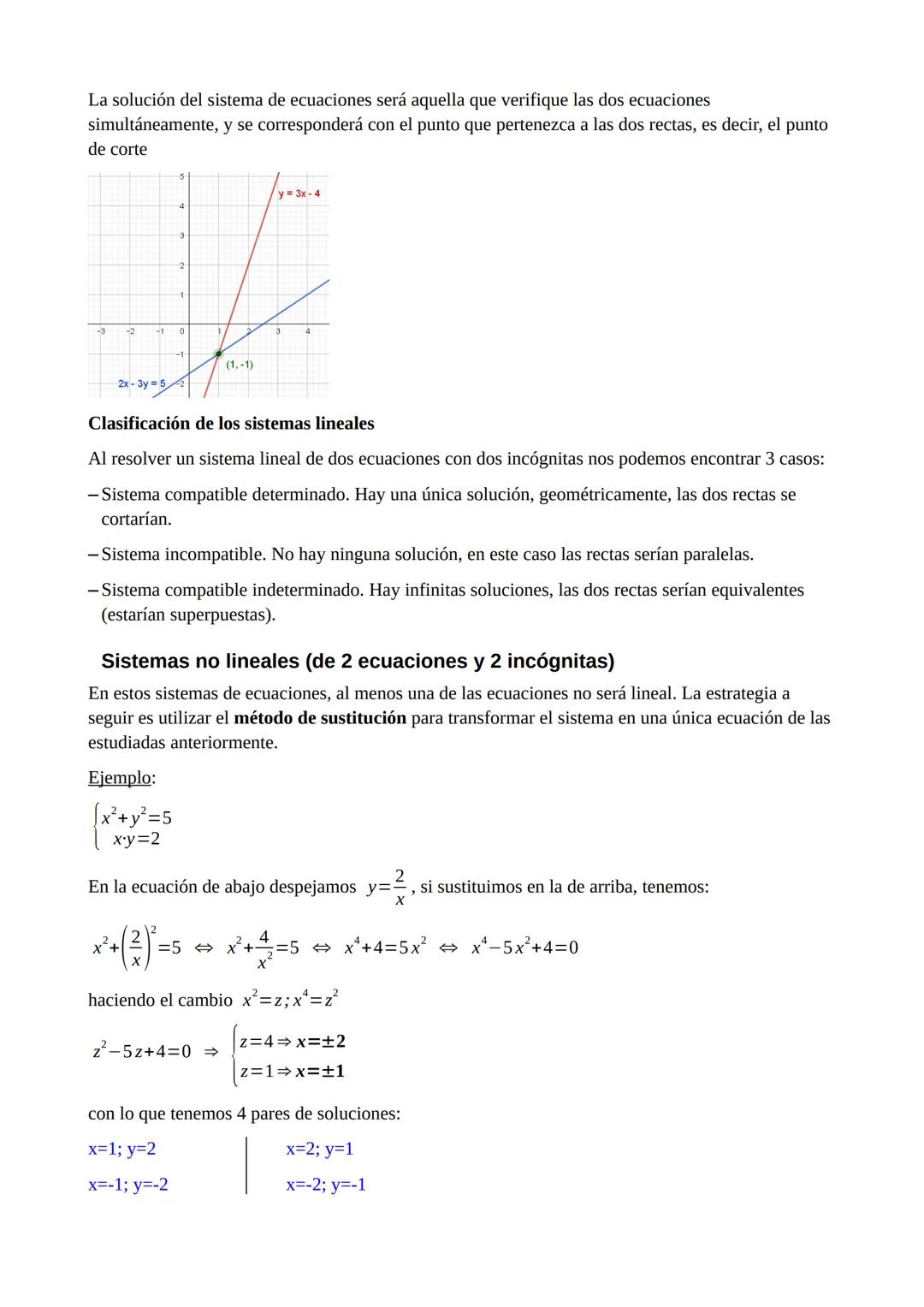
Los sistemas lineales 2x2 los dominas con tres métodos clásicos: sustitución, igualación y reducción. Geométricamente, cada ecuación es una recta, y la solución es donde se cruzan.

Puedes tener tres situaciones: una solución única (rectas que se cortan), ninguna solución (rectas paralelas), o infinitas soluciones (rectas superpuestas). Esto te da sistemas compatibles determinados, incompatibles o compatibles indeterminados.

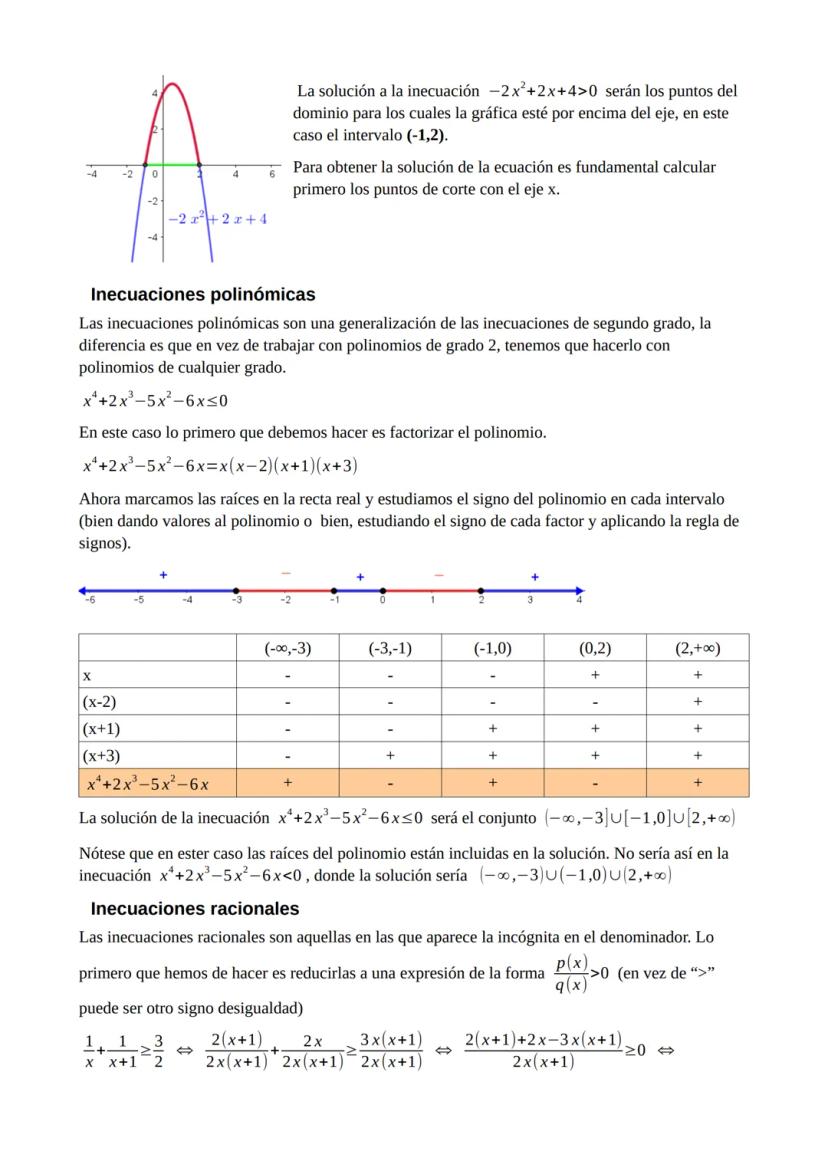
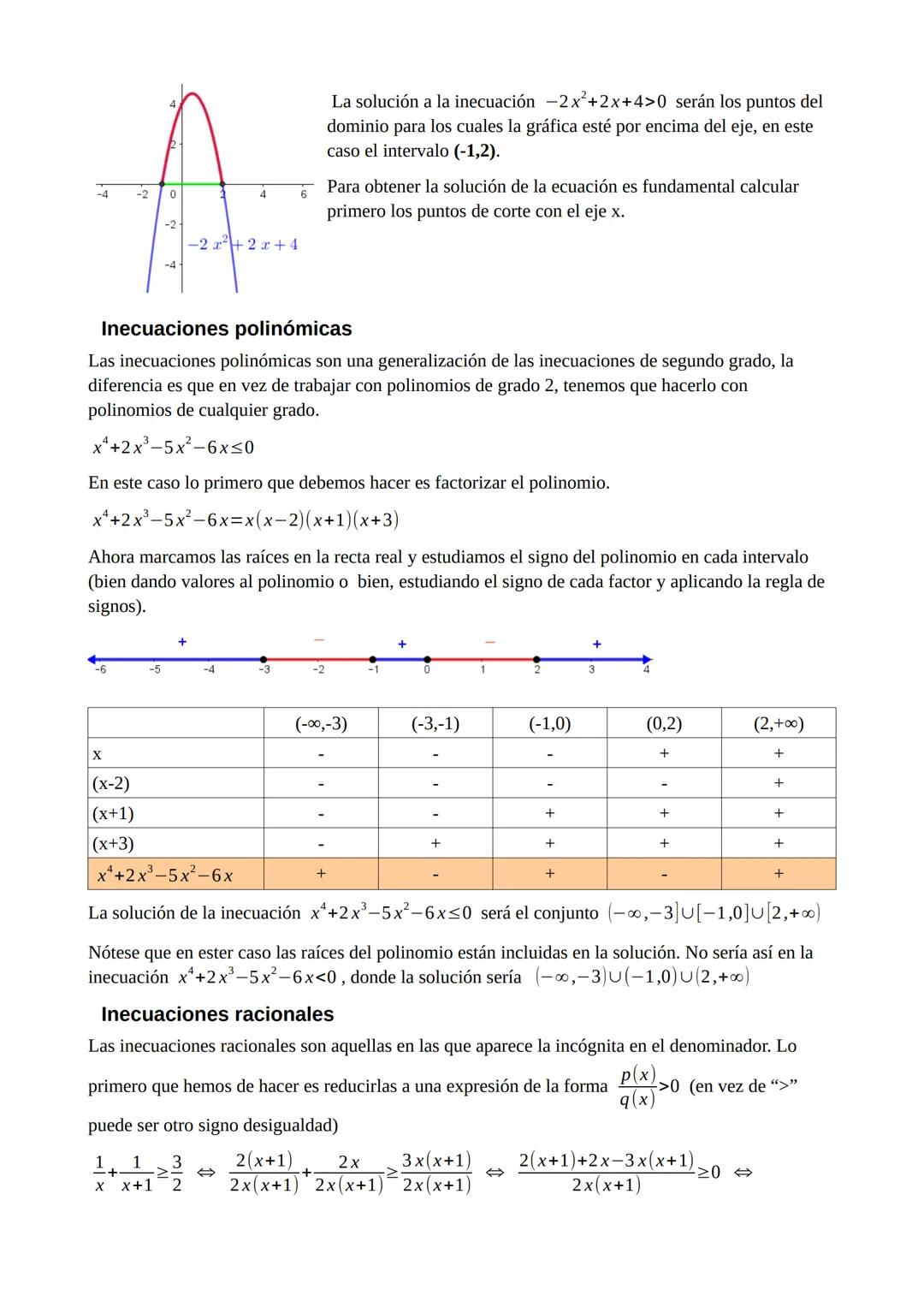
Los sistemas no lineales se atacan principalmente por sustitución. Despejas una variable de la ecuación más sencilla y la sustituyes en la otra. Esto puede generar ecuaciones bicuadradas o de otros tipos que ya sabes resolver.

En sistemas no lineales, puedes obtener múltiples soluciones. Por ejemplo, si una ecuación representa una circunferencia y otra una hipérbola, pueden cortarse en varios puntos.

Tip geométrico: Visualizar qué representan las ecuaciones te ayuda a entender cuántas soluciones esperar.

Sistemas lineales 3x3 y método de Gauss

El método de Gauss es tu arma secreta para sistemas grandes. Consiste en triangularizar: conseguir que la primera ecuación tenga tres incógnitas, la segunda dos, y la tercera solo una.

Usas operaciones elementales: multiplicar una ecuación por una constante, sumar o restar ecuaciones entre sí. El objetivo es crear ceros estratégicamente para simplificar el sistema paso a paso.

Una vez triangularizado, resuelves "hacia atrás". Empiezas por la última ecuación (que tiene una sola incógnita), después sustituyes en la anterior, y así sucesivamente.

Los sistemas 3x3 también se clasifican en los tres tipos habituales. Si aparece 0 = k (con k ≠ 0), es incompatible. Si aparece 0 = 0, tienes infinitas soluciones y necesitas parámetros.

Organización clave: Mantén las operaciones ordenadas y claras. Un error pequeño se amplifica en todo el sistema.

Inecuaciones lineales y de segundo grado

Las inecuaciones lineales se resuelven como ecuaciones, pero con una regla de oro: al multiplicar o dividir por un número negativo, cambia el sentido de la desigualdad. Este es el error más común, ¡no caigas en él!

Las soluciones de inecuaciones son intervalos, no números puntuales. Usa la notación de intervalos correctamente: corchetes para "incluido" y paréntesis para "no incluido".

Para inecuaciones de segundo grado, el truco está en la representación gráfica. El polinomio de segundo grado es una parábola, y necesitas los intervalos donde está por encima o por debajo del eje X.

Primero encuentra las raíces (donde la parábola corta el eje X), después estudia el signo en cada intervalo. Si la parábola abre hacia arriba, será positiva en los extremos y negativa en el medio.

Visualización ganadora: Dibuja siempre la parábola. Te ayuda a ver claramente dónde está la solución.

Inecuaciones polinómicas y racionales

Las inecuaciones polinómicas generalizan el concepto anterior a cualquier grado. Tu estrategia: factoriza completamente el polinomio y estudia el signo en cada intervalo determinado por las raíces.

Crea una tabla de signos con cada factor por separado, después aplica la regla de signos para obtener el signo del polinomio completo. Esto te dice exactamente en qué intervalos es positivo o negativo.

Las inecuaciones racionales añaden la complicación del denominador. Primero reduce todo a la forma P(x)/Q(x) ≥ 0, después factoriza numerador y denominador por separado.

Aquí hay una diferencia crucial: las raíces del denominador nunca pueden formar parte de la solución, porque harían la fracción indefinida. Márcalas con paréntesis abiertos siempre.

Detalle importante: En racionales, las raíces del numerador sí pueden estar en la solución (si el signo lo permite), pero las del denominador jamás.

Sistemas de inecuaciones e inecuaciones con dos incógnitas

Los sistemas de inecuaciones son súper directos: resuelves cada inecuación por separado y después haces la intersección de las soluciones. La solución final es donde se cumplen todas a la vez.

Representa cada solución en la recta real y encuentra la zona común. Si no hay intersección, el sistema no tiene solución.

Las inecuaciones con dos incógnitas cambian completamente el juego. Ahora las soluciones son regiones del plano, no intervalos de la recta.

Para inecuaciones lineales, la solución es un semiplano. Primero dibuja la recta frontera $cambiando ≥ por =$, después determina qué lado del plano es la solución probando un punto de prueba.

Método infalible: Usa siempre el punto (0,0) como punto de prueba, a menos que esté en la recta frontera.

Inecuaciones lineales en el plano

Representar inecuaciones lineales con dos incógnitas es como colorear regiones del plano. La ecuación correspondiente $sustituyendo ≥ por =$ te da la recta frontera que divide el plano en dos semiplanos.

Para saber cuál es el semiplano solución, elige un punto que no esté en la recta (normalmente el origen funciona bien) y evalúa si cumple la inecuación. Si la cumple, colorea ese lado; si no, colorea el otro.

Si el signo es ≥ o ≤, la recta frontera forma parte de la solución (dibújala continua). Si es > o <, la recta no está incluida (dibújala discontinua o punteada).

Los sistemas de inecuaciones con dos incógnitas crean regiones poligonales. Cada inecuación delimita un semiplano, y la solución es la intersección de todos ellos.

Consejo visual: Usa colores diferentes para cada inecuación. La zona donde se superponen todos los colores es tu solución final.