Programación Lineal
La programación lineal es una técnica para optimizar (encontrar máximos o mínimos) de una función lineal sujeta a restricciones también lineales. Esta herramienta es fundamental para resolver problemas de optimización en situaciones reales.
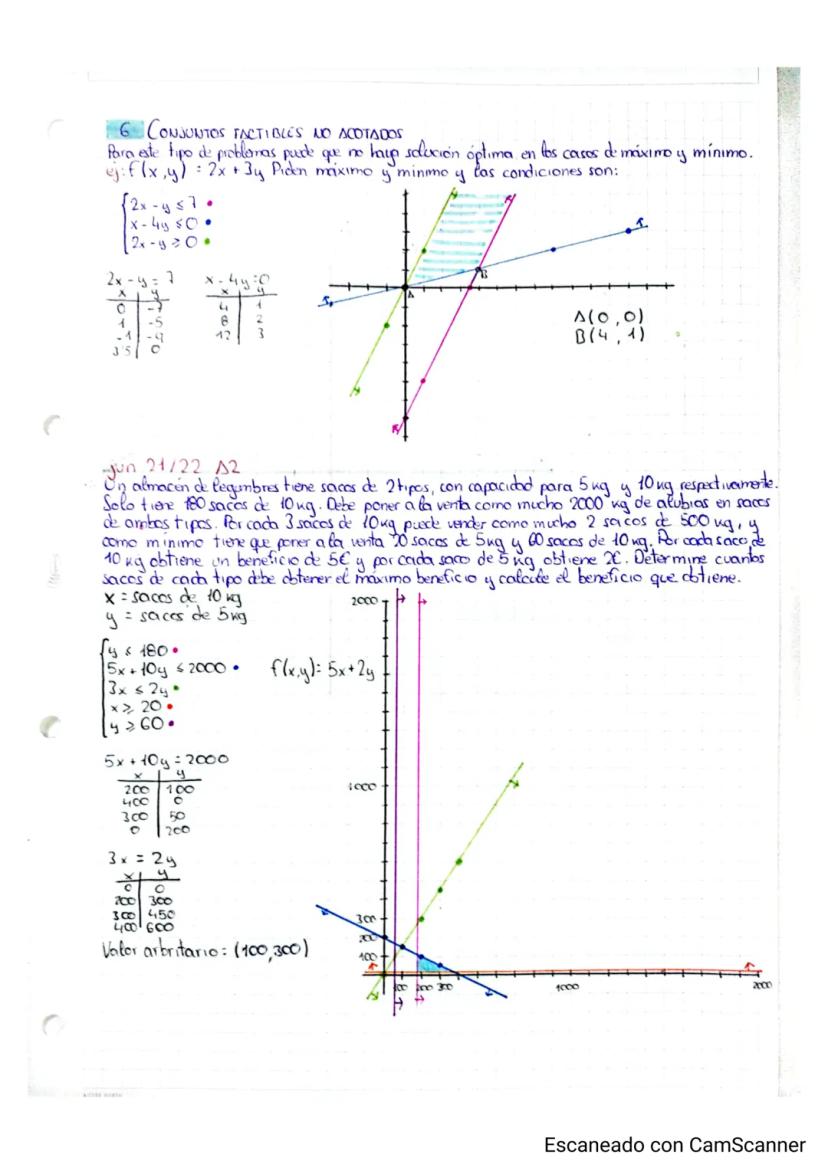
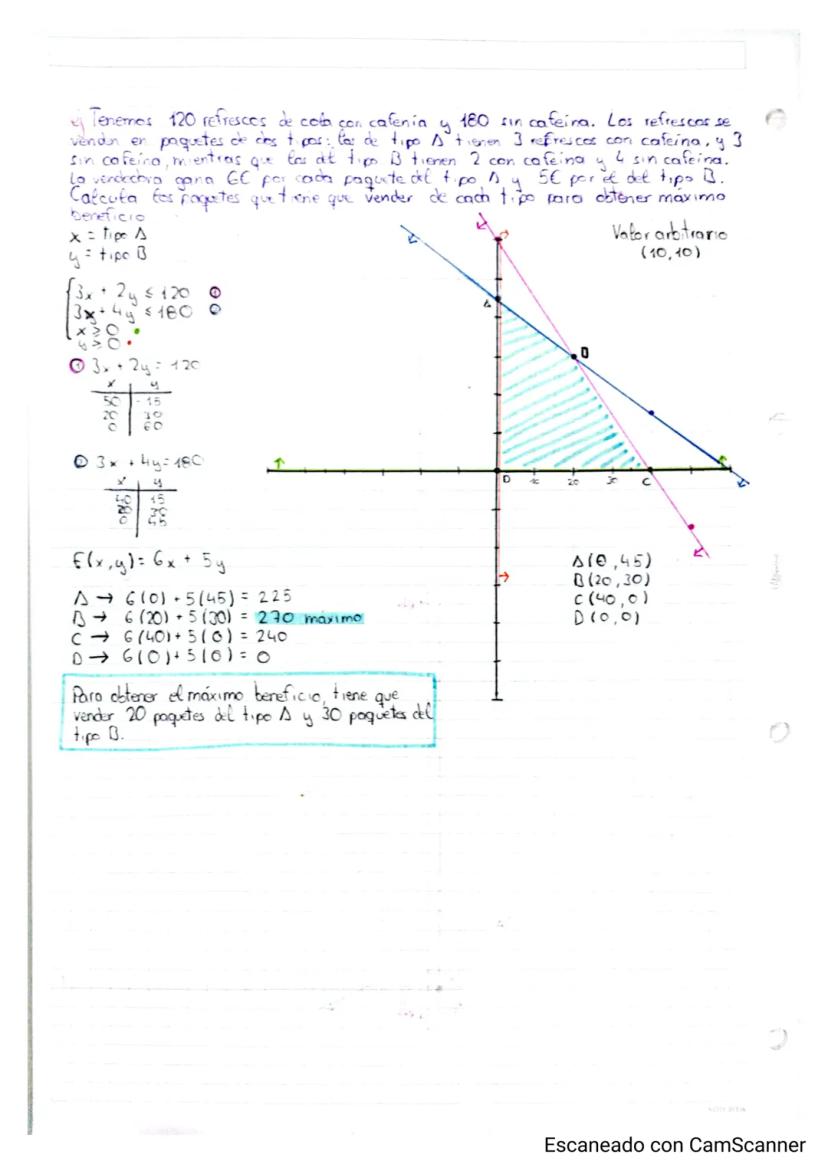
El procedimiento para resolver problemas de programación lineal consiste en representar gráficamente la región factible delimitada por las restricciones, identificar sus vértices y evaluar la función objetivo en estos puntos. El valor óptimo (máximo o mínimo) siempre se encontrará en alguno de los vértices.
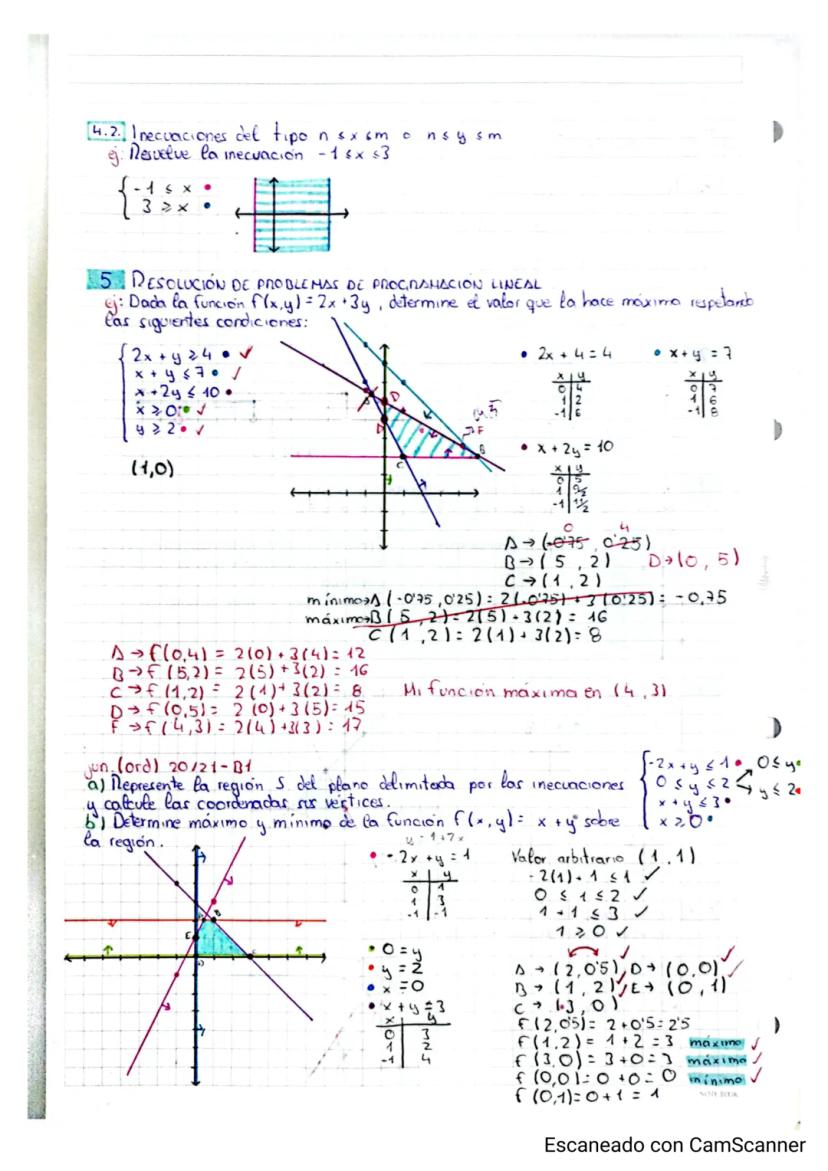
Por ejemplo, para maximizar la función f(x,y) = 2x + 3y sujeta a varias restricciones, primero graficamos todas las ecuaciones correspondientes a las restricciones (2x + y = 4, x + y = 7, etc.), identificamos los vértices de la región factible, y evaluamos la función en cada vértice. El valor máximo en este caso es 16, que se alcanza en el punto (5,2).
🔍 Observación clave: En problemas de programación lineal, los valores óptimos (máximos o mínimos) siempre se alcanzan en los vértices de la región factible, nunca en puntos intermedios.
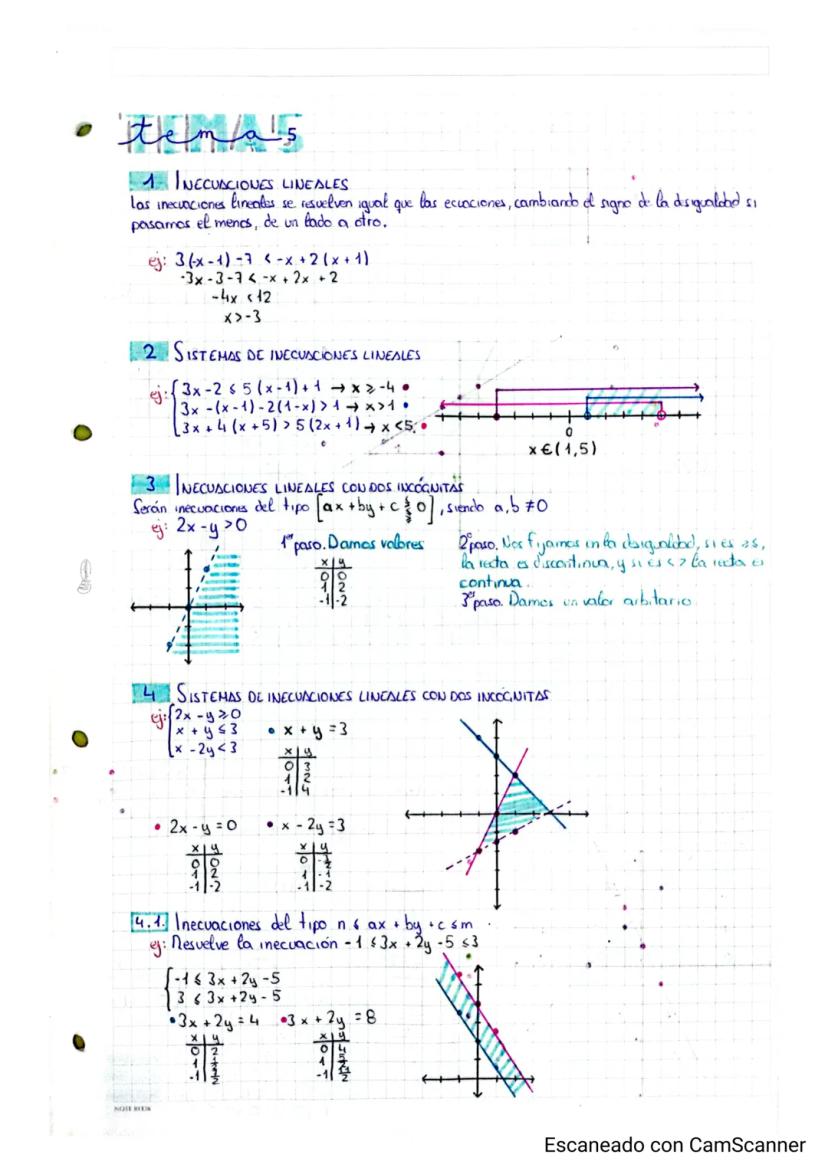
Algunos casos especiales incluyen las inecuaciones del tipo n ≤ x ≤ m, que representan bandas horizontales o verticales en el plano, y deben tratarse como dos restricciones separadas (n ≤ x y x ≤ m).