Funciones Arco (Trigonométricas Inversas)
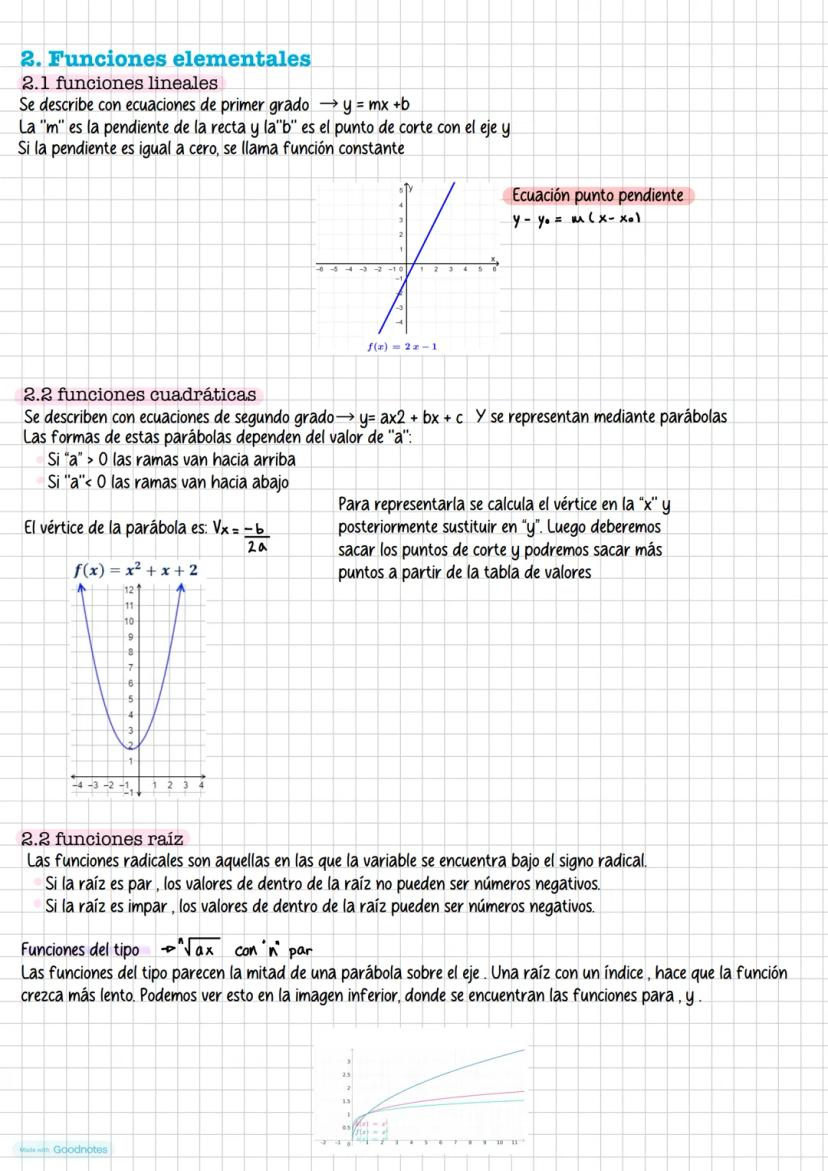
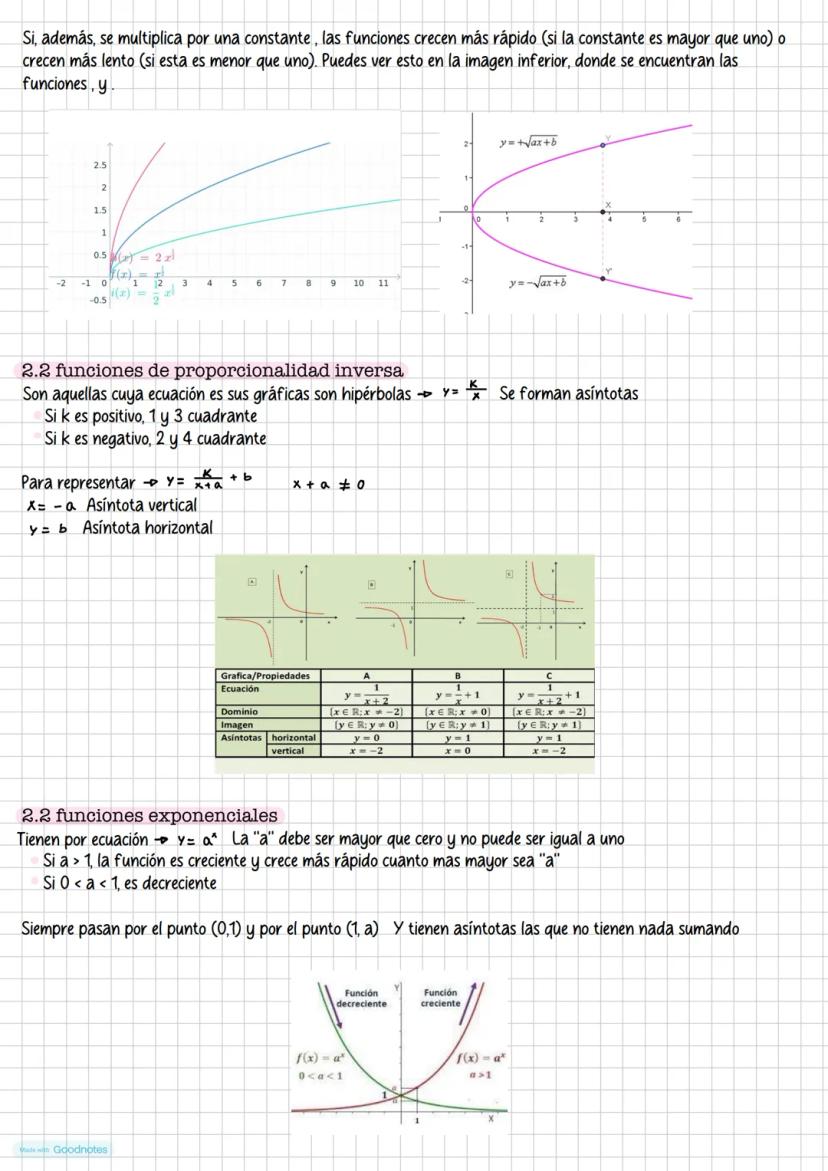
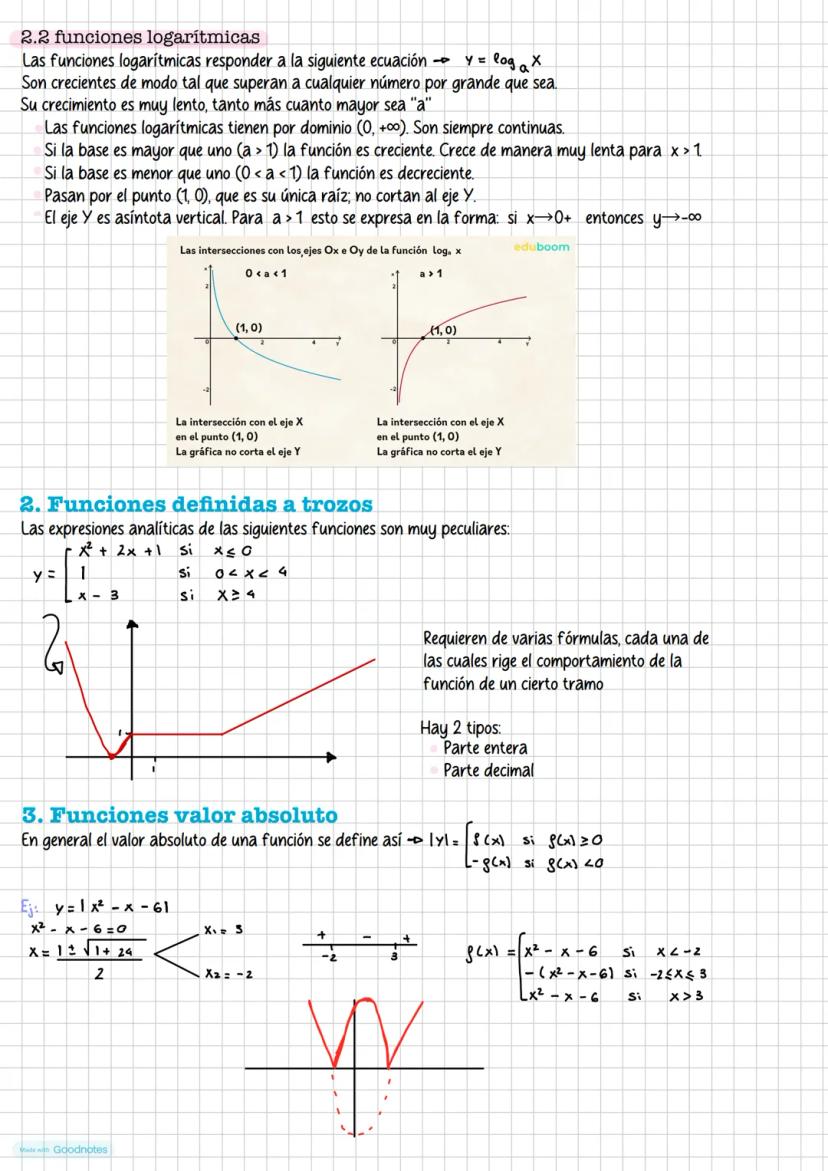
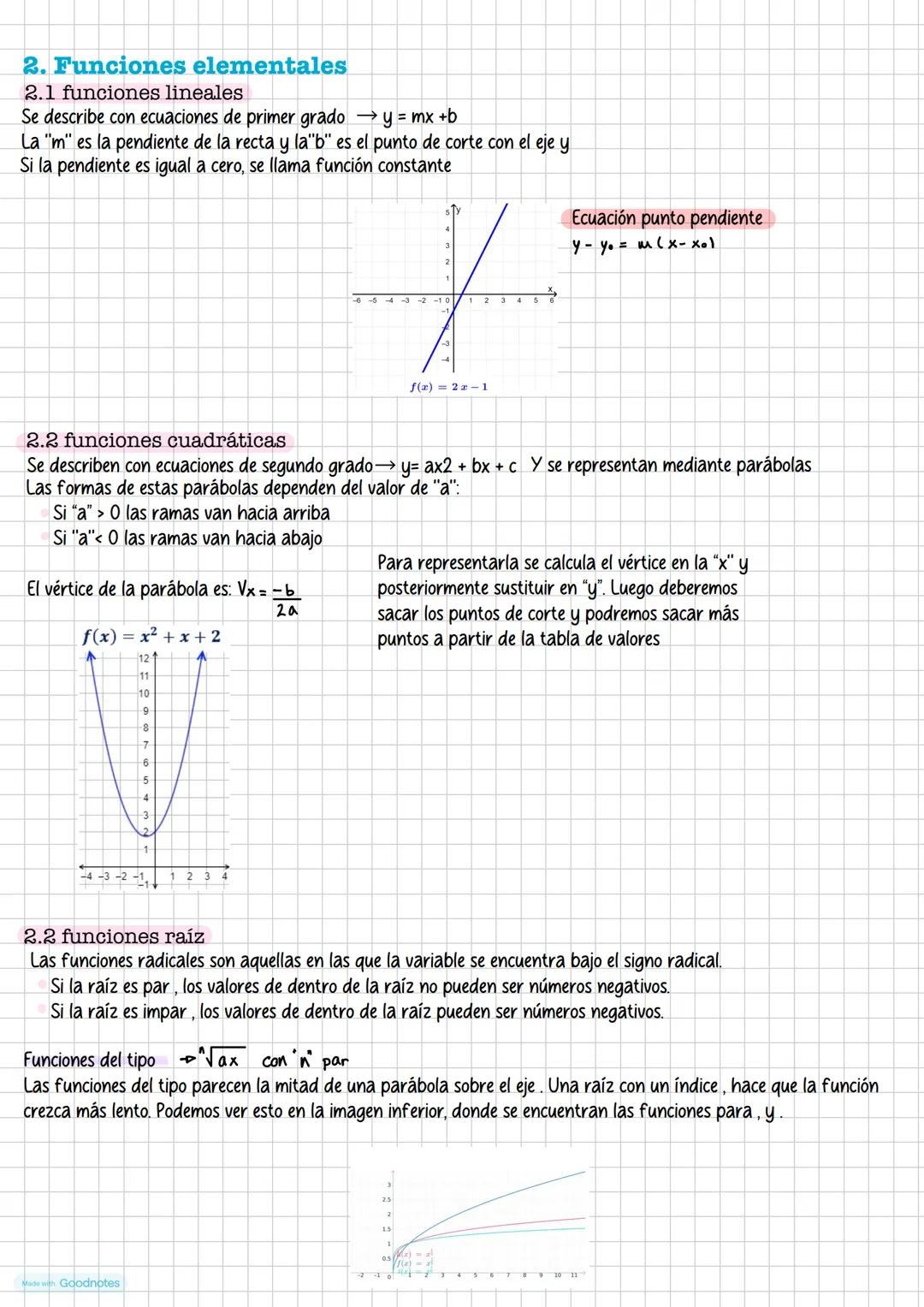
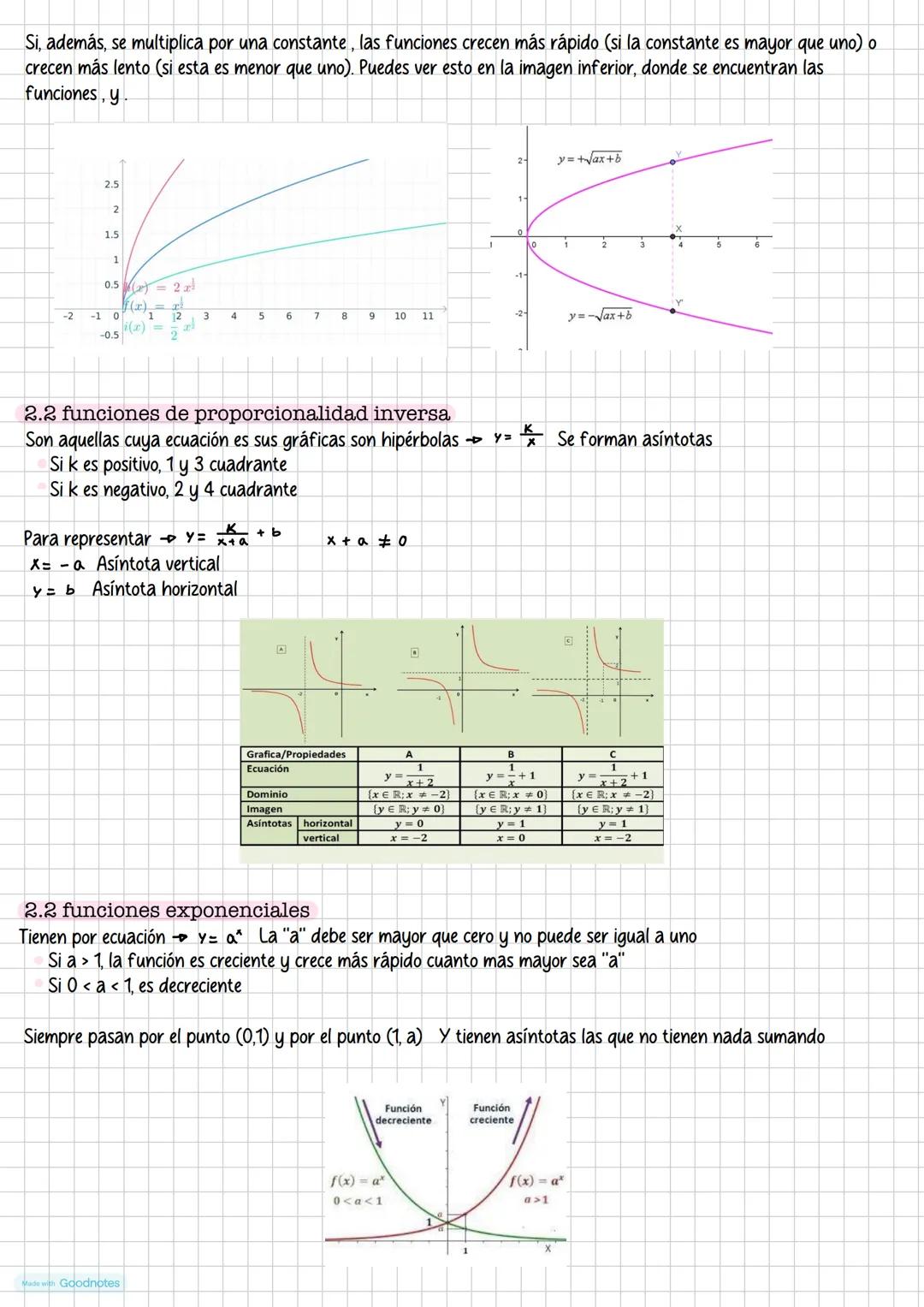
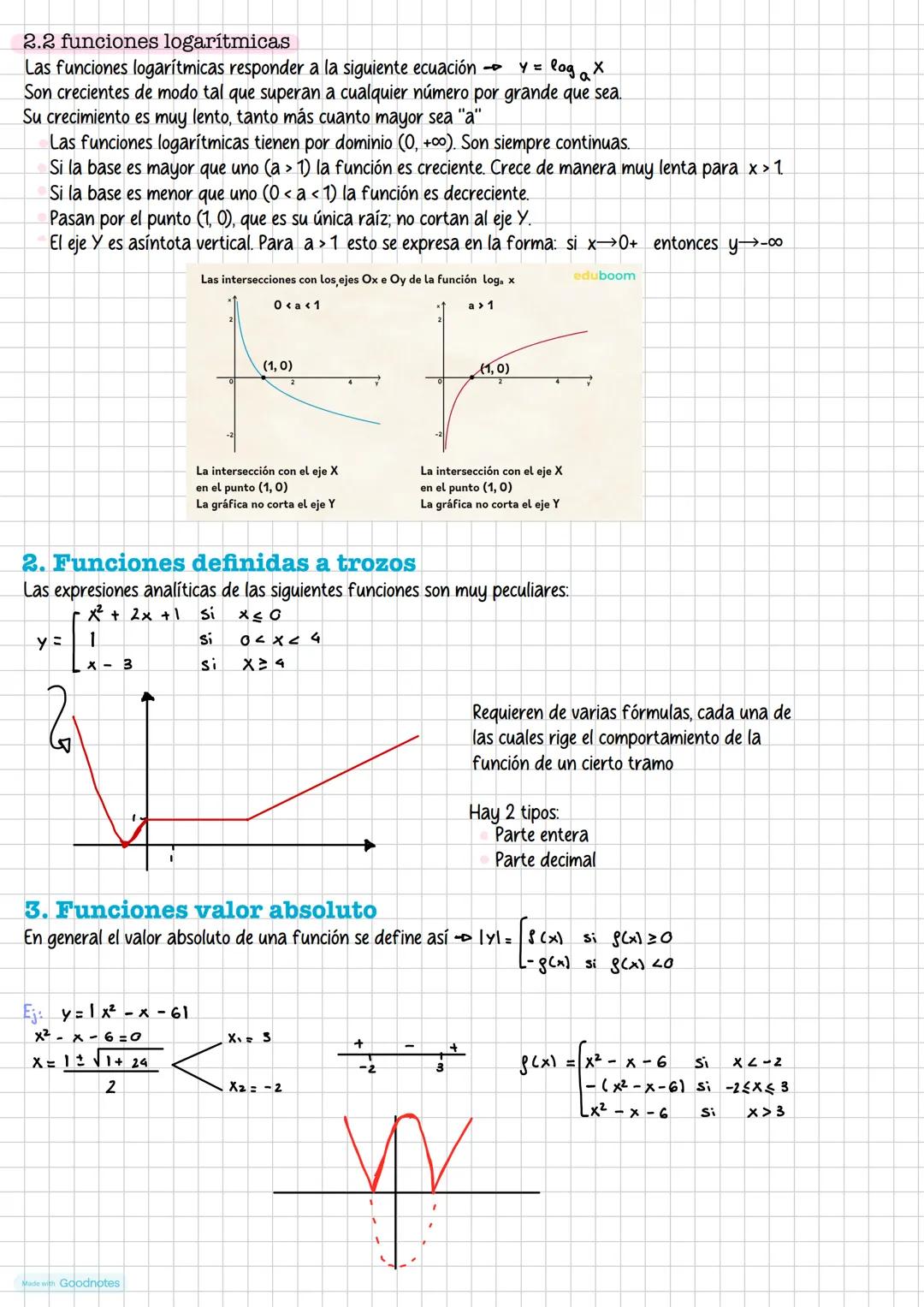
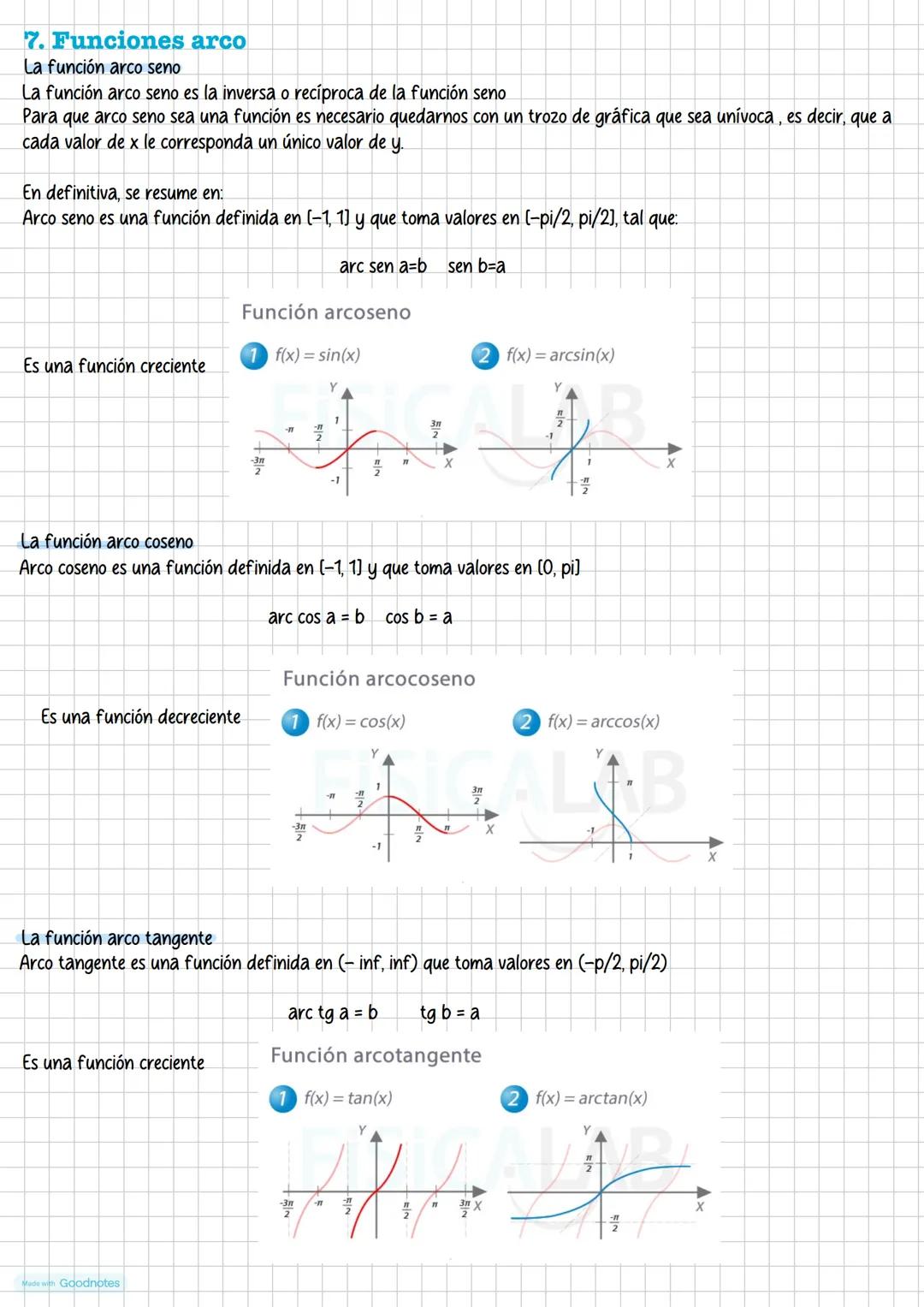
Las funciones arco son las inversas de las funciones trigonométricas. Como las funciones trigonométricas no son inyectivas en todo su dominio, debemos restringirlas a intervalos apropiados.
Arcoseno: dominio [-1,1], rango [-π/2, π/2], función creciente. Arcocoseno: dominio [-1,1], rango [0, π], función decreciente. Arcotangente: dominio (-∞,∞), rango (-π/2, π/2), función creciente.
Estas funciones son esenciales para resolver ecuaciones trigonométricas y encontrar ángulos cuando conoces las razones trigonométricas.
📌 Recuerda: arc sen a = b significa que sen b = a. Es decir, arcoseno te da el ángulo cuyo seno es el valor dado.