Empezar

Física

Tipos de Magnitudes Físicas

Física y Química215Actualizado 4 oct 20264 páginas

Magnitudes Escalares y Vectoriales en Física 4°ESO

Denunciar
user profile picture
Lucía@_lucii_18
Añadir a fuentes de Google
¿Alguna vez te has preguntado por qué necesitas tanto el número como la dirección para explicar la velocidad de un coche? En física, trabajamos con dos tipos de magnitudes muy diferentes: escalares y vectoriales. Dominar estos conceptos te dará las herramientas para entender cómo se mueven los objetos en el mundo real.
Magnitudes escalares y vectoriales. – página 1

Inscríbete para ver los apuntes.
¡Es gratis!

Al registrarte aceptas las Condiciones del servicio y la Política de privacidad.

Magnitudes Escalares y Vectoriales

Las magnitudes escalares son las más sencillas: solo necesitas un número y su unidad. Piensa en tu edad (16 años), el tiempo que tardas en llegar al instituto (20 minutos) o la masa de tu mochila (3 kg). ¡Pan comido!

Las magnitudes vectoriales son más complejas pero mucho más interesantes. Necesitas tres cosas: el módulo (el valor numérico), la dirección (la línea donde actúa) y el sentido (hacia dónde apunta la flecha). La velocidad es el ejemplo perfecto: no es lo mismo ir a 50 km/h hacia el norte que hacia el sur.

Operaciones con vectores que debes dominar: cuando multiplicas un vector por un escalar, cambias su tamaño pero mantienes su dirección. Si multiplicas por -1, obtienes el vector opuesto. Para sumar vectores, si van en la misma dirección, sumas sus módulos; si son perpendiculares, usas el teorema de Pitágoras: S=a2+b2S = \sqrt{a^2+b^2}.

💡 Truco clave: En los exámenes, siempre dibuja los vectores primero. Te ayudará a visualizar el problema y evitar errores.

Magnitudes escalares y vectoriales. – página 2

Inscríbete para ver los apuntes.
¡Es gratis!

Al registrarte aceptas las Condiciones del servicio y la Política de privacidad.

Descomposición de Vectores y Cinemática Básica

Cuando los vectores forman ángulos raros, necesitas descomponerlos en componentes. Es como dividir una fuerza diagonal en sus partes horizontal y vertical. Usas seno y coseno: bx=bcos⁡αb_x = b \cos α y by=bsin⁡αb_y = b \sin α. Luego sumas las componentes por separado.

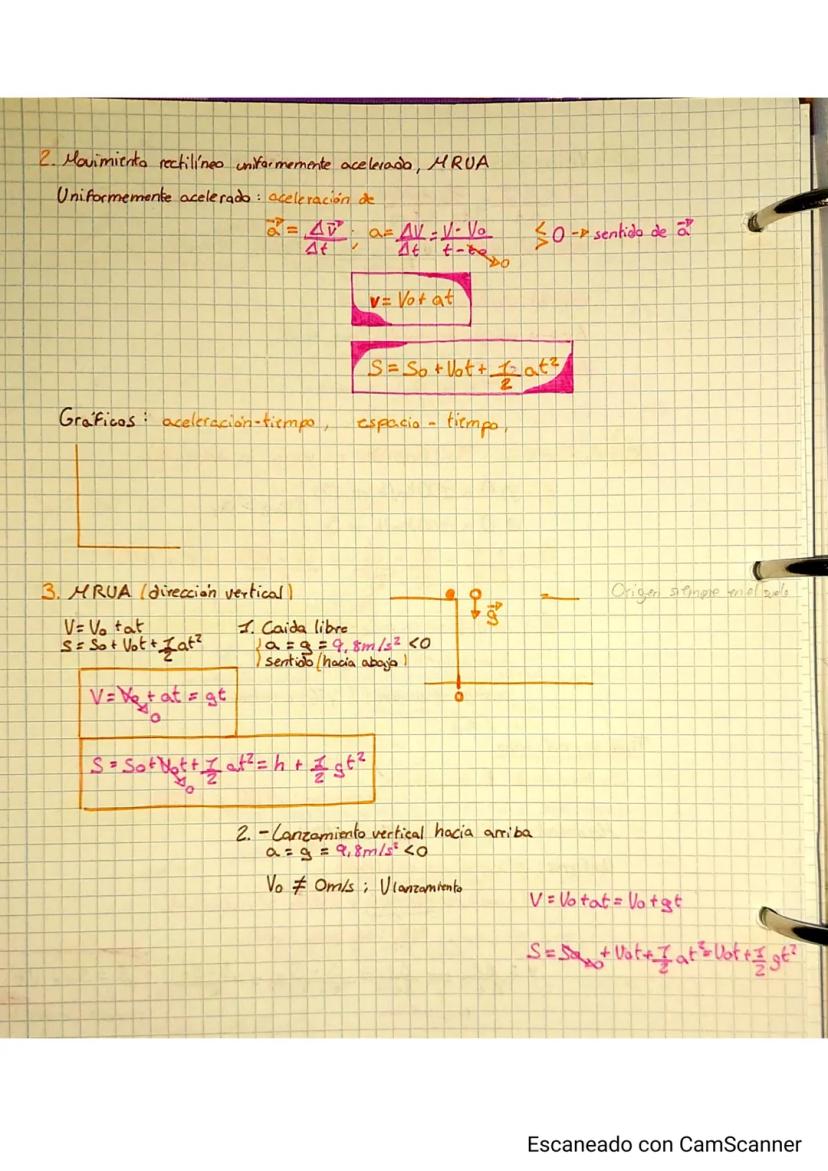
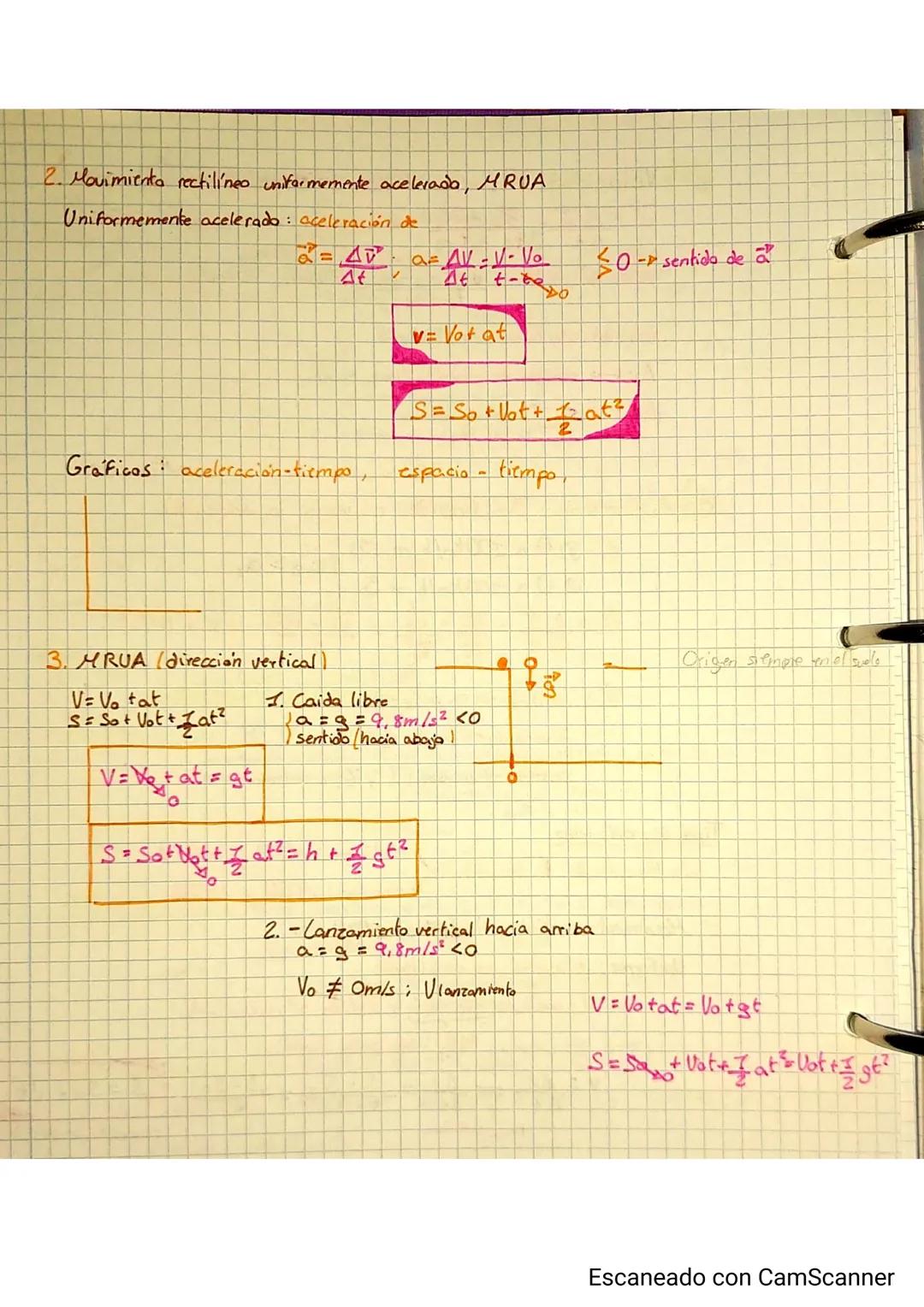
La posición siempre depende de tu sistema de referencia: ¿desde dónde mides? Puede ser unidimensional (solo eje x), bidimensional (x,y) o tridimensional (x,y,z). El movimiento siempre es relativo al observador.

La trayectoria es la línea imaginaria que describe el móvil. Puede ser rectilínea (MRU, MRUA) o curvilínea (circular, parabólica). El desplazamiento Δx=x2−x1Δx = x_2 - x_1 te dice cuánto cambió la posición, no la distancia recorrida.

💡 Dato importante: El desplazamiento puede ser negativo, cero o positivo según la dirección del movimiento.

Magnitudes escalares y vectoriales. – página 3

Inscríbete para ver los apuntes.
¡Es gratis!

Al registrarte aceptas las Condiciones del servicio y la Política de privacidad.

Velocidad, Aceleración y MRU

La velocidad (V=ΔxΔtV = \frac{Δx}{Δt}) mide qué tan rápido cambias de posición. No confundas velocidad media con velocidad instantánea: la primera es un promedio, la segunda es lo que marca el velocímetro en un momento exacto.

La aceleración (a=ΔvΔta = \frac{Δv}{Δt}) indica qué tan rápido cambia tu velocidad. Un deportivo que pasa de 0 a 100 km/h en 4 segundos tiene mayor aceleración que uno que tarda 8 segundos. Su unidad es m/s².

El Movimiento Rectilíneo Uniforme (MRU) es el más simple: velocidad constante, aceleración cero. Su ecuación clave es s=s0+vts = s_0 + vt. En las gráficas posición-tiempo obtienes una línea recta, y en velocidad-tiempo una línea horizontal.

💡 Para exámenes: En MRU, la pendiente de la gráfica posición-tiempo te da directamente la velocidad.

Magnitudes escalares y vectoriales. – página 4

Inscríbete para ver los apuntes.
¡Es gratis!

Al registrarte aceptas las Condiciones del servicio y la Política de privacidad.

Movimiento Rectilíneo Uniformemente Acelerado (MRUA)

En el MRUA la aceleración es constante, pero la velocidad cambia linealmente. Las ecuaciones fundamentales son: v=v0+atv = v_0 + at y s=s0+v0t+12at2s = s_0 + v_0t + \frac{1}{2}at^2. Memorízalas porque las usarás constantemente.

Caída libre: es MRUA vertical con a=g=9.8m/s2a = g = 9.8 m/s^2 hacia abajo. Un objeto que sueltas desde cierta altura tiene v0=0v_0 = 0, así que v=gtv = gt y h=12gt2h = \frac{1}{2}gt^2. ¡Sencillo!

Lanzamiento vertical hacia arriba: también es MRUA con gg negativo, pero ahora v0≠0v_0 ≠ 0. El objeto sube, se frena, se para y cae. En el punto más alto, v=0v = 0 pero a=−ga = -g sigue actuando.

💡 Consejo práctico: En problemas de lanzamiento vertical, encuentra primero el tiempo de vuelo cuando la posición vuelve a ser la inicial.

Pensamos que nunca lo preguntarías...

Nuestro compañero de IA está específicamente adaptado a las necesidades de los estudiantes. Basándonos en los millones de contenidos que tenemos en la plataforma, podemos dar a los estudiantes respuestas realmente significativas y relevantes. Pero no se trata solo de respuestas, el compañero también guía a los estudiantes a través de sus retos de aprendizaje diarios, con planes de aprendizaje personalizados, cuestionarios o contenidos en el chat y una personalización del 100% basada en las habilidades y el desarrollo de los estudiantes.

Puedes descargar la app en Google Play Store y Apple App Store.

Sí, tienes acceso gratuito a los contenidos de la aplicación y a nuestro compañero de IA. Para desbloquear determinadas funciones de la aplicación, puedes adquirir Knowunity Pro.

Contenido similar

Física y Química

MAGNITUDES FÍSICAS Y VECTORES

Tipos de magnitudes físicas y operaciones con vectores

4° ESO9178
Física i Química

VECTORES

Apuntes en GALLEGO de los vectores, sus componentes y operaciones con ellos.

4° ESO2364
Física i Química

Física

Resumen primero bachillerato

1° Bach3774
Física

Magnitudes vectoriales: características y representación

Aprende sobre las características fundamentales de los vectores y cómo se representan en una figura pictórica.

2° Bach13123
Física i Química

El movimiento y la energía

Mapa conceptual sobre el movimiento y la energía de física

4° ESO108423
Física i Química

TEORÍA DE HIBRIDACIÓN

Ejemplos

1° Bach72415
Ver más

Contenidos más populares: Vector

Física y Química

MAGNITUDES FÍSICAS Y VECTORES

Tipos de magnitudes físicas y operaciones con vectores

4° ESO9178
Física i Química

VECTORES

Apuntes en GALLEGO de los vectores, sus componentes y operaciones con ellos.

4° ESO2364
Física i Química

El movimiento y la energía

Mapa conceptual sobre el movimiento y la energía de física

4° ESO108423
Física i Química

Física

Resumen primero bachillerato

1° Bach3774

Contenidos más populares: Física y Química

Física y Química

Formulación compuestos inorgánicos

óxidos, peróxidos, hidruros metálicos y no metálicos, sales binarias, hidróxidos, sales ácidas, oxosales, iones y oxoacidos

1° Bach209952
Física y Química

Formulación orgánica apuntes con ejercicios

apuntes bien redactados y hechos

1° Bach306367
Física y Química

Formulación Inorgánica Química 1°BACH

Guía con lo necesario para formular y trucos

1° Bach29.2572002
Química

Formulación orgánica

Apuntes de formulación orgánica para 1-2 Bachillerato

1° Bach4144103
Física y Química

Formulación

Aquí tienes todos los pasos para aprender formulación

4° ESO5236
Física y Química

Química Orgánica

Apuntes sobre cómo hacer química orgánico con ejemplos

4° ESO235272
Física y Química

La estructura del átomo

Esquema del tema estructura del átomo para selectividad (temario 1º Bachillerato)

1° Bach91930
Física y Química

Modelos atómicos

Teoría de Dalton, Modelo atómico de Thomson, modelo atómico de Rutherford, modelo atómico de Bohr, modelo atómico cuántico actual

3° ESO204259
Física y Química

Formulación orgánica teoría y ejercicios

1bachillerato

1° Bach2217158

Contenidos más populares

Otros

Carnet Conducir

Apuntes permiso de conducir tipo B

2° Bach9921241
Otros

Apuntes examen teórico de coche

Os dejo por aquí apuntes hechos por mi de lo imprescindible para obtener el apto en el examen teórico del permiso b.

PAU (2° Bach)8321211
Tips de estudio

Apuntes teorico carnet de conducir ACTUALIZADO

sacate el teorico con estos apuntes!!!

2° Bach5762157
Química

Formulación inorgánica 1-2 Bachillerato

Apuntes para Química y PAU

1° Bach4411129
Otros

Apuntes Teorico Permiso B

Examen Teorico del Coche

2° Bach5991126
Inglés

Tiempos verbales en inglés

Están los tiempos verbales desde el presente, el pasado y el futuro

2° Bach359990
Filosofía

Platón

Platón (biografía,teoría de las ideas y teoría del conocimiento, antropología y política)

2° Bach5191117
Filosofía

TEMA 1: LA FILOSOFÍA DE PLATÓN

TEMA 1: LA FILOSOFÍA DE PLATÓN 1. Biografía 2. La teoría de las ideas 3. Conocimiento y realidad 4. Ser humano 5. Ética 6. Sociedad y política

2° Bach12.069497
Inglés

Inglés temario entero

Contiene: tiempos verbales, condicionales, time clauses, wish clauses, pasiva, causativa, relative clauses, modals & modals perfects y reported speech.

4° ESO174967

Mira lo que dicen nuestros usuarios. Les encanta - y a tí también.

4.6/5App Store
4.7/5Google Play
Pablousuario de iOS

La app es muy fácil de usar y está muy bien diseñada. Hasta ahora he encontrado todo lo que estaba buscando y he podido aprender mucho de las presentaciones. Definitivamente utilizaré la aplicación para un examen de clase. Y, por supuesto, también me sirve mucho de inspiración.

Elenausuaria de Android

Esta app es realmente genial. Hay tantos apuntes de clase y ayuda [...]. Tengo problemas con matemáticas, por ejemplo, y la aplicación tiene muchas opciones de ayuda. Gracias a Knowunity, he mejorado en mates. Se la recomiendo a todo el mundo.

Anausuaria de iOS

Vaya, estoy realmente sorprendida. Acabo de probar la app porque la he visto anunciada muchas veces y me he quedado absolutamente alucinada. Esta app es LA AYUDA que quieres para el insti y, sobre todo, ofrece muchísimas cosas, como ejercicios y hojas informativas, que a mí personalmente me han sido MUY útiles.