Resolución de Inecuaciones con Valor Absoluto
Las inecuaciones con valor absoluto tienen patrones que puedes memorizar fácilmente. Para |x-a| < r, la solución es a−r,a+r. Para |x-a| > r, la solución es −∞,a−r ∪ a+r,+∞.
Cuando tengas expresiones más complejas, descompón el valor absoluto según su definición. Por ejemplo, |x+3| < 5 se convierte en -5 < x+3 < 5, que da -8 < x < 2.
Para casos como |3-x| < 4, reescríbelo como |-x−3| = |x-3| < 4, y entonces -4 < x-3 < 4, lo que da -1 < x < 7.
🔑 Clave: Siempre dibuja la solución en la recta numérica para verificar que tenga sentido









![- EVALUACION
UNIDAD 1: N° Reales
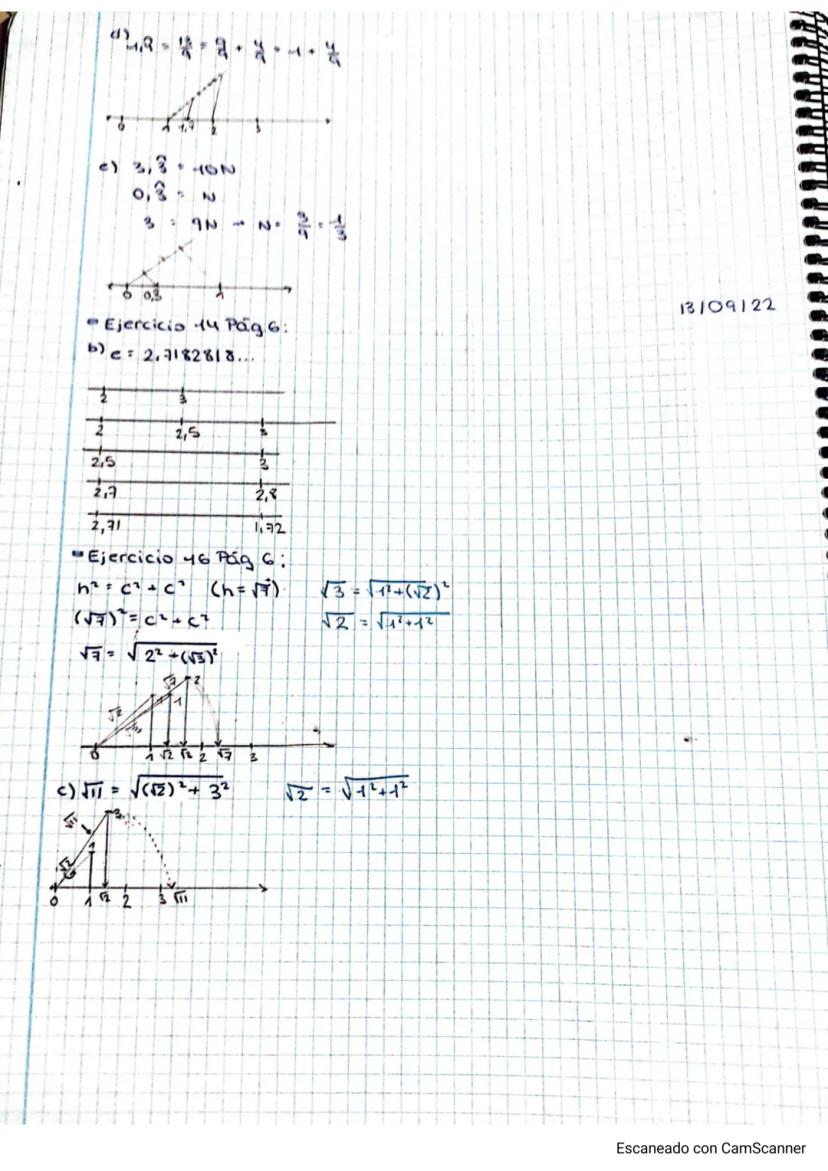
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_1.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_2.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_3.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_4.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_5.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_6.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_7.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_8.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_9.webp&w=2048&q=75)
![- EVALUACION
UNIDAD 1: N° Reales
- Ejercicio 49 Pág 14:
a) $\sqrt[5]{2^3\sqrt{2}\sqrt{2}} = \sqrt[5]{2^3 2^{\frac{1}{2}} 2^{\frac{1}{4}}}](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FKXalumODdZjOlGCipOyp_image_page_10.webp&w=2048&q=75)