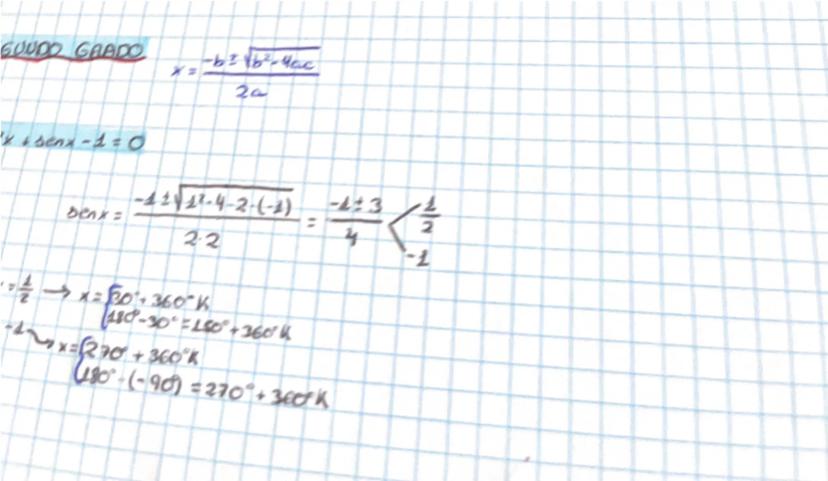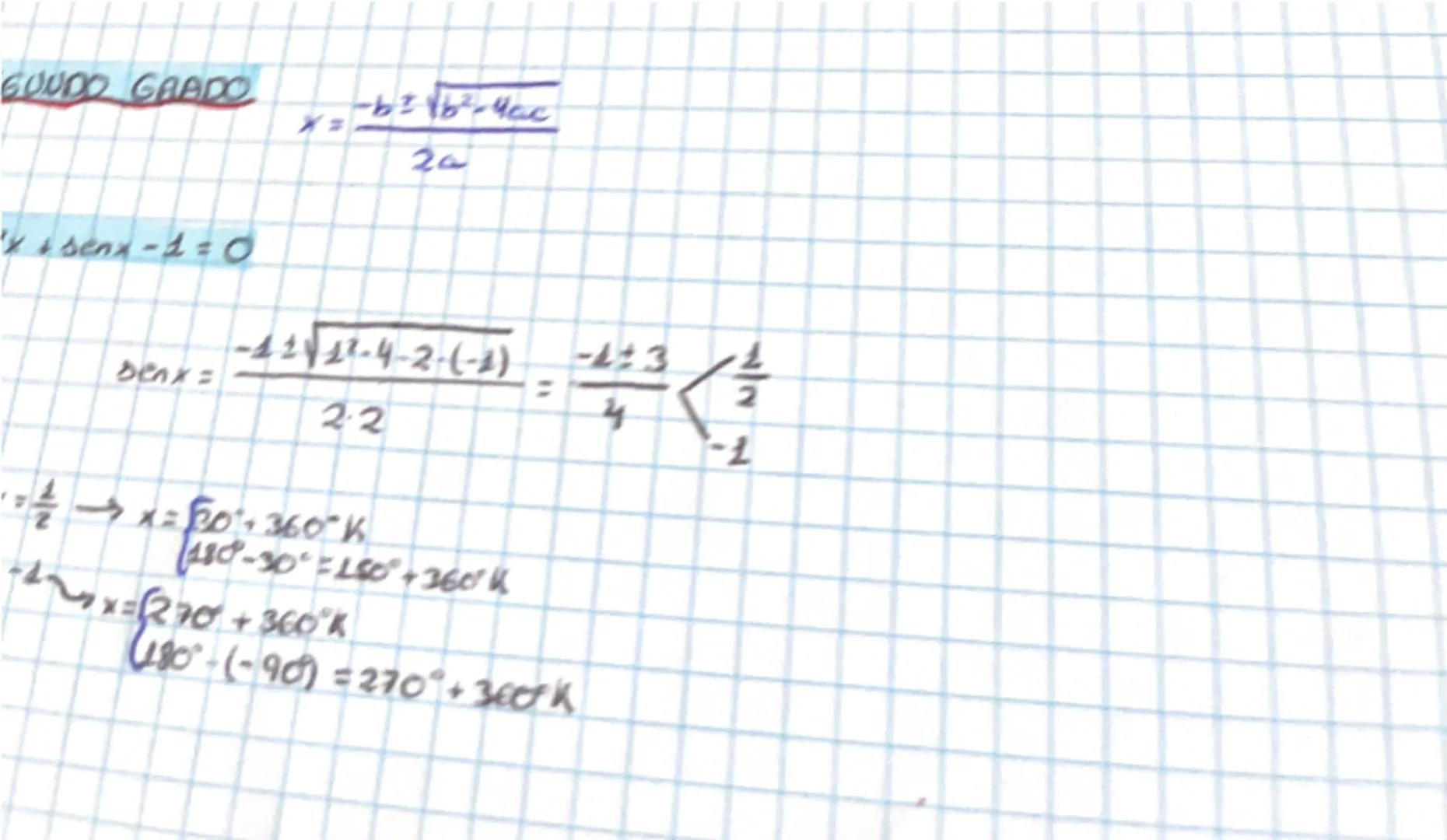Matemáticas

Funciones e Identidades Trigonométricas

funciones trigonométricas

Matemáticas1103Actualizado 31 ago 202610 páginas

Trigonometría Explicada: Fórmulas y Conceptos Claves

Denunciar

🙃@holy_moly

Añadir a fuentes de Google

¡La trigonometría no tiene por qué ser tu pesadilla! En estas páginas vas a descubrir cómo dominar desde los conceptos más básicos hasta resolver ecuaciones complejas. Te aseguro que con las fórmulas y técnicas que verás aquí, podrás enfrentarte a cualquier problema trigonométrico del examen.

Inscríbete para ver los apuntes.
¡Es gratis!

Ángulos y Razones Trigonométricas Básicas

¿Sabías que puedes medir ángulos de dos formas completamente diferentes? Los grados (que ya conoces) y los radianes son como dos idiomas distintos para hablar de lo mismo.

Para convertir entre ellos, recuerda que 360° = 2π radianes. Así, 45° se convierte en π/4 radianes, y 3π radianes son 270°. Tu calculadora científica hace estas conversiones automáticamente siguiendo los pasos indicados.

Las razones trigonométricas (seno, coseno y tangente) son las herramientas básicas que necesitas dominar. En un triángulo rectángulo: sen = cateto opuesto/hipotenusa, cos = cateto adyacente/hipotenusa, y tan = cateto opuesto/cateto adyacente.

¡Truco! Para resolver triángulos rectángulos solo necesitas conocer dos datos: la hipotenusa y un cateto, dos catetos, la hipotenusa y un ángulo, o un cateto y un ángulo. ¡Con eso ya puedes encontrar todo lo demás!

Inscríbete para ver los apuntes.
¡Es gratis!

Resolución de Triángulos: Casos Especiales

Cuando tienes un triángulo rectángulo, puedes usar el teorema de Pitágoras y las razones trigonométricas básicas. Pero ¿qué pasa cuando el triángulo no tiene ángulo recto?

Para triángulos cualquiera necesitas armas más potentes: el teorema del seno y el teorema del coseno. El teorema del seno dice que a/senA = b/senB = c/senC, y es perfecto cuando conoces algunos lados y ángulos opuestos.

El teorema del coseno (a² = b² + c² - 2bc·cosA) es tu mejor aliado cuando tienes dos lados y el ángulo entre ellos, o cuando conoces los tres lados. Es como una versión mejorada del teorema de Pitágoras.

¡Importante! Siempre recuerda que en cualquier triángulo, la suma de los ángulos internos es 180°. Esto te ayudará a encontrar el tercer ángulo fácilmente.

Inscríbete para ver los apuntes.
¡Es gratis!

Aplicaciones Prácticas de la Trigonometría

La trigonometría no es solo teoría aburrida, ¡tiene aplicaciones súper útiles en la vida real! Puedes calcular la altura de una montaña, la anchura de un río o la distancia entre dos puntos inaccesibles.

Para medir la altura de una montaña, necesitas dos ángulos de elevación desde puntos separados una distancia conocida. Usas las relaciones h/ $x+d$ = tg α y h/x = tg β para resolverlo.

La anchura de un río se calcula formando un triángulo donde conoces un lado (la distancia que caminas por la orilla) y dos ángulos. Aplicas el teorema del seno para encontrar la anchura.

¡Dato curioso! Los agrimensores, arquitectos e ingenieros usan estas técnicas constantemente. ¡Estás aprendiendo matemáticas que se usan en profesiones reales!

Inscríbete para ver los apuntes.
¡Es gratis!

Razones Trigonométricas en la Circunferencia Unitaria

Imagínate una circunferencia de radio 1 centrada en el origen. Aquí es donde la trigonometría se vuelve realmente poderosa, porque puedes trabajar con cualquier ángulo, no solo los de 0° a 90°.

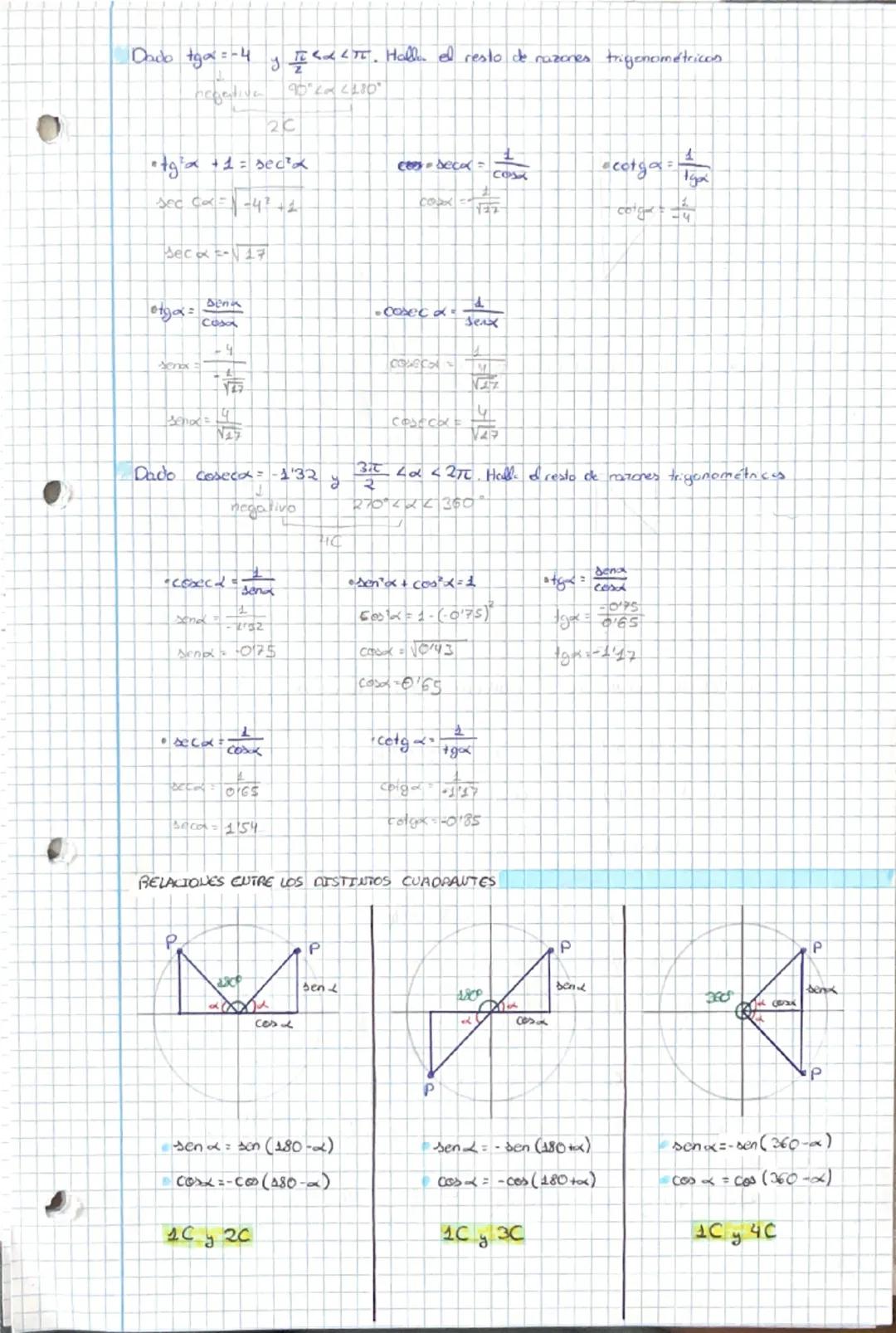
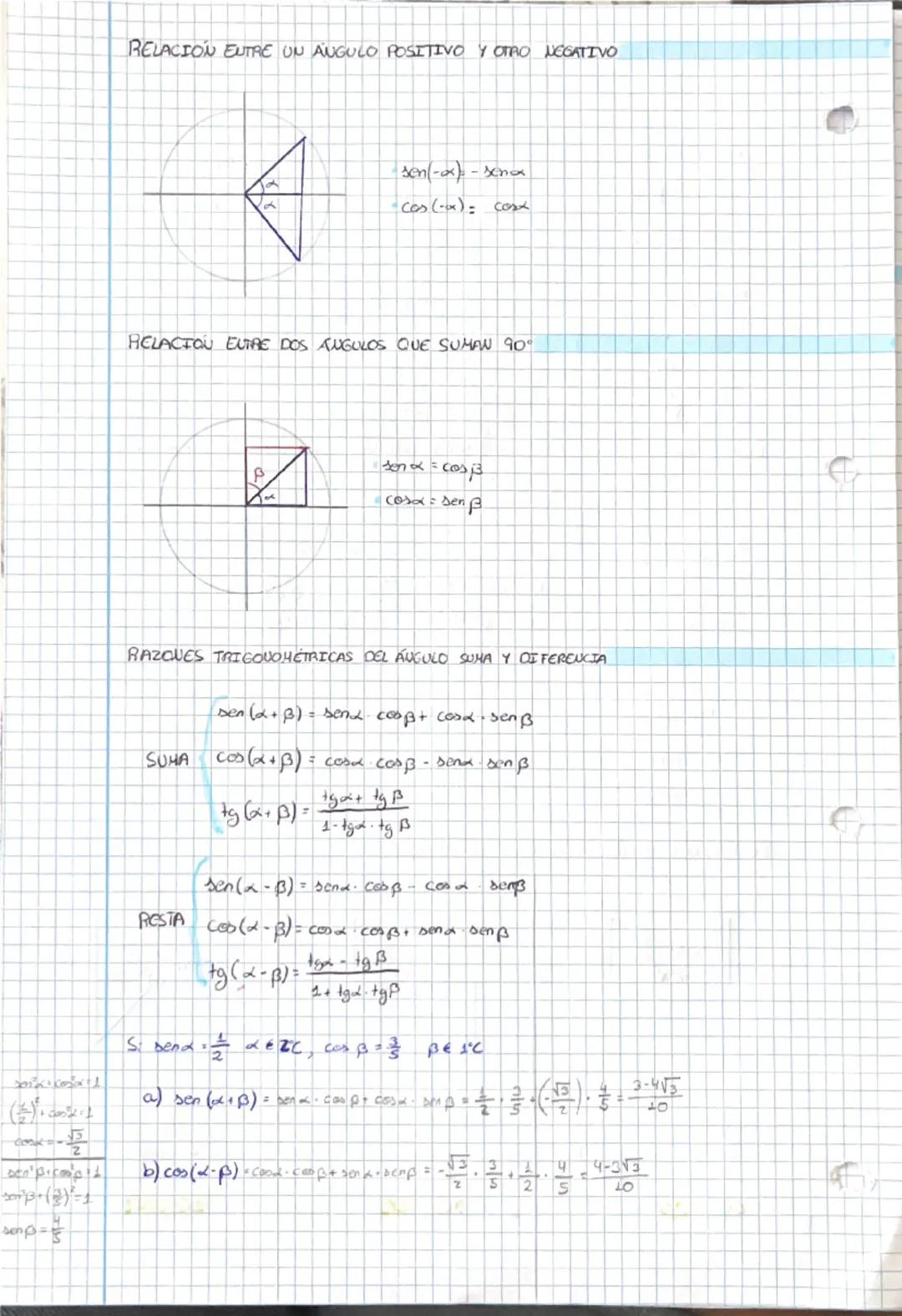
En cada cuadrante, el seno y coseno tienen diferentes signos: primer cuadrante (+,+), segundo cuadrante (+,-), tercer cuadrante (-,-), cuarto cuadrante (-,+). El punto P tiene coordenadas (cos x, sen x).

La relación fundamental sen²x + cos²x = 1 es tu mejor amiga. También tienes 1 + cotg²x = cosec²x y tg²x + 1 = sec²x. Con estas fórmulas puedes calcular todas las razones trigonométricas conociendo solo una.

¡Clave del éxito! El seno y coseno NUNCA pueden ser mayores que 1 en valor absoluto. Si te sale un resultado mayor, revisa tus cálculos.

Inscríbete para ver los apuntes.
¡Es gratis!

Relaciones Entre Cuadrantes

¿Te has preguntado cómo se relacionan los ángulos de diferentes cuadrantes? ¡Hay patrones súper útiles que te ahorrarán mucho tiempo!

Entre el primer y segundo cuadrante: sen x = sen $180° - x$ , pero cos x = -cos $180° - x$ . Entre el primer y tercer cuadrante: ambos cambian de signo. Entre el primer y cuarto cuadrante: solo el seno cambia de signo.

Para ángulos negativos, recuerda que sen $-α$ = -sen α, pero cos $-α$ = cos α. Y cuando dos ángulos suman 90°, sus senos y cosenos se intercambian: sen α = cos β y cos α = sen β.

¡Estrategia ganadora! Memoriza los signos de cada cuadrante con la regla "Solo Todos Con Tangente": en el 1er cuadrante todo es positivo, en el 2do solo seno, en el 3er solo tangente, en el 4to solo coseno.

Inscríbete para ver los apuntes.
¡Es gratis!

Fórmulas de Suma y Diferencia de Ángulos

Las fórmulas de suma y diferencia son herramientas increíblemente poderosas que te permiten descomponer ángulos complejos en otros más simples.

Para la suma: sen $α + β$ = sen α cos β + cos α sen β, y cos $α + β$ = cos α cos β - sen α sen β. Para la diferencia, cambias algunos signos: sen $α - β$ = sen α cos β - cos α sen β.

La tangente tiene su propia fórmula: tg $α + β$ = (tg α + tg β)/(1 - tg α · tg β). Estas fórmulas son especialmente útiles cuando trabajas con ángulos como 75° $45° + 30°$ o 15° $45° - 30°$ .

¡Consejo pro! Practica estas fórmulas con ángulos conocidos como 30°, 45° y 60°. Una vez que domines los cálculos básicos, los problemas complejos se vuelven mucho más fáciles.

Inscríbete para ver los apuntes.
¡Es gratis!

Ángulo Doble, Mitad e Identidades

El ángulo doble tiene fórmulas específicas súper útiles: sen(2x) = 2sen x cos x, cos(2x) = cos²x - sen²x, y tg(2x) = 2tg x/ $1 - tg²x$ . Estas aparecen constantemente en los exámenes.

Para el ángulo mitad usas las raíces: sen $x/2$ = ±√ $(1-cos x)/2$ y cos $x/2$ = ±√ $(1+cos x)/2$ . El signo depende del cuadrante donde esté x/2.

Las identidades trigonométricas son igualdades que siempre se cumplen. Para demostrarlas, transforma un lado hasta que sea igual al otro usando las relaciones fundamentales. Es como resolver un puzzle matemático.

¡Técnica infalible! Para las identidades, trabaja siempre con el lado más complicado primero. Usa las relaciones fundamentales y las definiciones básicas para simplificar paso a paso.

Inscríbete para ver los apuntes.
¡Es gratis!

Ecuaciones Trigonométricas Básicas

Las ecuaciones trigonométricas te piden encontrar todos los ángulos que satisfacen una condición. La clave está en recordar que las funciones trigonométricas son periódicas.

Para ecuaciones tipo seno: sen x = a tiene soluciones x = arcsen $a$ + 360°k y x = 180° - arcsen $a$ + 360°k, donde k es cualquier número entero.

Para ecuaciones tipo coseno: cos x = a da x = arccos $a$ + 360°k y x = -arccos $a$ + 360°k. Para la tangente: tg x = a resulta en x = arctg $a$ + 180°k.

¡Atención especial! Siempre verifica que tus soluciones estén en el intervalo pedido. Las funciones trigonométricas se repiten, así que puede haber infinitas soluciones teóricas.

Inscríbete para ver los apuntes.
¡Es gratis!

Ecuaciones Trigonométricas de Segundo Grado

Cuando aparece una ecuación trigonométrica cuadrática como 2sen²x + sen x - 1 = 0, trata la función trigonométrica como una variable normal.

Sustituye sen x = t y resuelve la ecuación cuadrática 2t² + t - 1 = 0 usando la fórmula general. Obtienes t = 1/2 y t = -1, que significa sen x = 1/2 y sen x = -1.

Ahora resuelves cada ecuación trigonométrica básica por separado. sen x = 1/2 da x = 30° + 360°k y x = 150° + 360°k. sen x = -1 da x = 270° + 360°k.

¡Método infalible! Siempre haz la sustitución primero, resuelve la ecuación algebraica, y luego regresa a las ecuaciones trigonométricas básicas. ¡No te saltes pasos!

Inscríbete para ver los apuntes.
¡Es gratis!

Resolución Completa de Ecuaciones Cuadráticas

El proceso para resolver ecuaciones trigonométricas de segundo grado es sistemático y predecible. Primero identificas los coeficientes a, b y c, luego aplicas la fórmula cuadrática.

En el ejemplo 2sen²x + sen x - 1 = 0, tienes a = 2, b = 1, c = -1. La fórmula te da sen x = $-1 ± 3$ /4, resultando en sen x = 1/2 y sen x = -1.

Cada valor obtenido genera sus propias soluciones trigonométricas. sen x = 1/2 corresponde a 30° y 150° (más sus múltiplos de 360°), mientras que sen x = -1 solo da 270° (más múltiplos de 360°).

¡Verificación final! Siempre sustituye tus respuestas en la ecuación original para comprobar que son correctas. Un pequeño error de cálculo puede llevarte por el camino equivocado.

Pensamos que nunca lo preguntarías...

Nuestro compañero de IA está específicamente adaptado a las necesidades de los estudiantes. Basándonos en los millones de contenidos que tenemos en la plataforma, podemos dar a los estudiantes respuestas realmente significativas y relevantes. Pero no se trata solo de respuestas, el compañero también guía a los estudiantes a través de sus retos de aprendizaje diarios, con planes de aprendizaje personalizados, cuestionarios o contenidos en el chat y una personalización del 100% basada en las habilidades y el desarrollo de los estudiantes.

Puedes descargar la app en Google Play Store y Apple App Store.

Sí, tienes acceso gratuito a los contenidos de la aplicación y a nuestro compañero de IA. Para desbloquear determinadas funciones de la aplicación, puedes adquirir Knowunity Pro.

Trigonometría Explicada: Fórmulas y Conceptos Claves

Ángulos y Razones Trigonométricas Básicas

Resolución de Triángulos: Casos Especiales

Aplicaciones Prácticas de la Trigonometría

Razones Trigonométricas en la Circunferencia Unitaria

Relaciones Entre Cuadrantes

Fórmulas de Suma y Diferencia de Ángulos

Ángulo Doble, Mitad e Identidades

Ecuaciones Trigonométricas Básicas

Ecuaciones Trigonométricas de Segundo Grado

Resolución Completa de Ecuaciones Cuadráticas

Pensamos que nunca lo preguntarías...

¿Qué es Knowunity AI companion?

¿Dónde puedo descargar la app Knowunity?

¿Knowunity es totalmente gratuito?

Contenido similar

Funciones elementales

Tema 4 - trigonometría

Trigonometría - RESUMEN - 4 ESO

Trigonometría

Trigonometría

Apuntes de Trigonometría 1 Bach

Contenidos más populares: funciones trigonométricas

Trigonometría - RESUMEN - 4 ESO

Tema 4 - trigonometría

Funciones elementales

Trigonometría

Trigonometría

Trigonometría

Contenidos más populares: Matemáticas

MATEMÁTICAS I

Trigonometría

MATES CIENCIAS 1 BACHILLERATO

Matemáticas II (análisis) 2Bach

Funciones, límites y continuidad

Matemática todo el curso

Matemáticas 2 Bachillerato completo (con probabilidad)

Potencias

Trigonométria 1 bach

Contenidos más populares

Carnet Conducir

Apuntes teorico carnet de conducir ACTUALIZADO

Apuntes examen teórico de coche

Apuntes Teorico Permiso B

Resumen completo carnet de conducir B – Esquemas y teoría explicada (40 pág)

INGLÉS B1 (Cambridge)

Teórico Coche B 2026

Inglés B2 (Parte 1)

Tiempos verbales en inglés

Mira lo que dicen nuestros usuarios. Les encanta - y a tí también.