Conceptos básicos: Radianes y razones trigonométricas
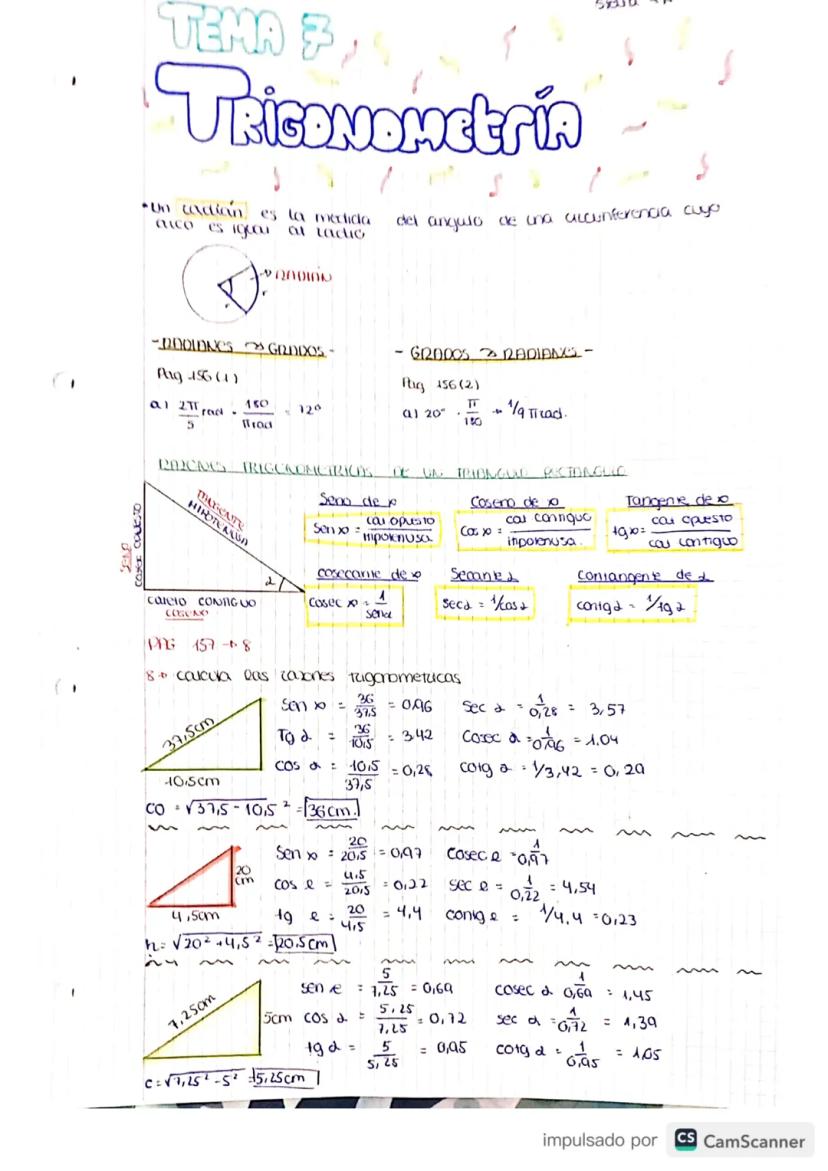
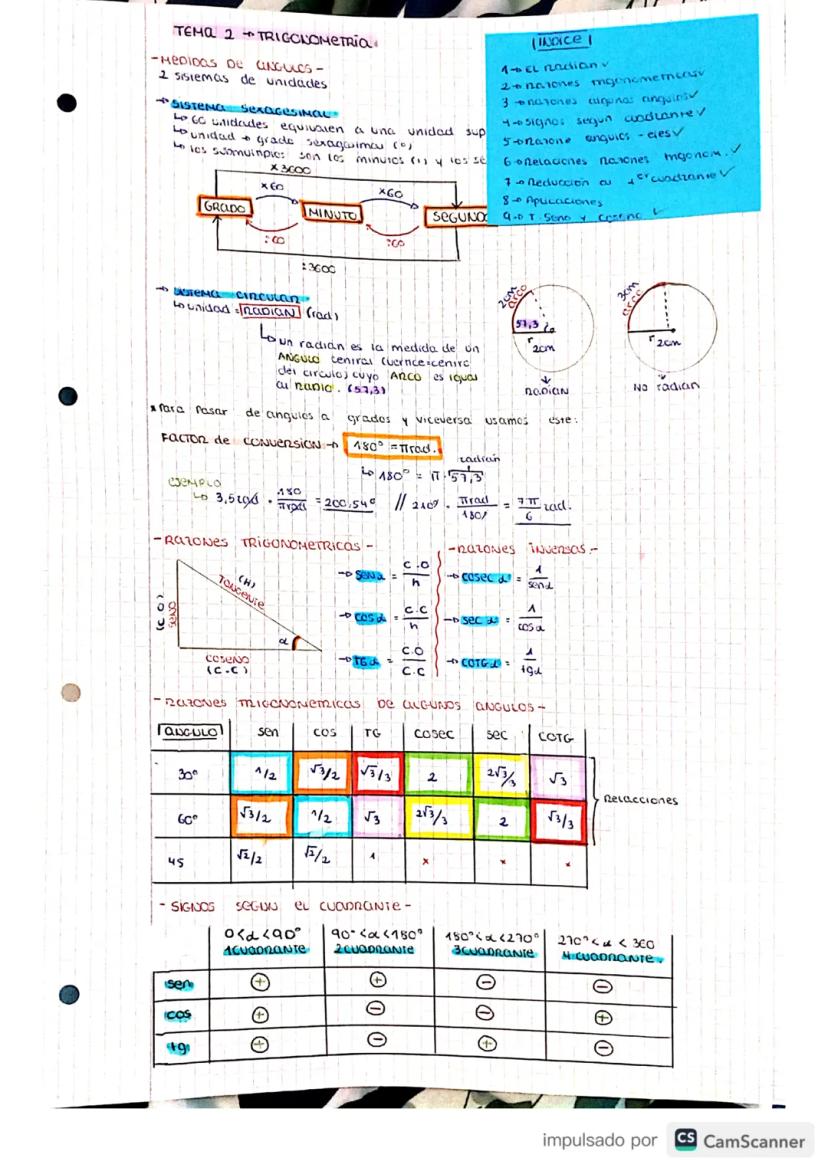
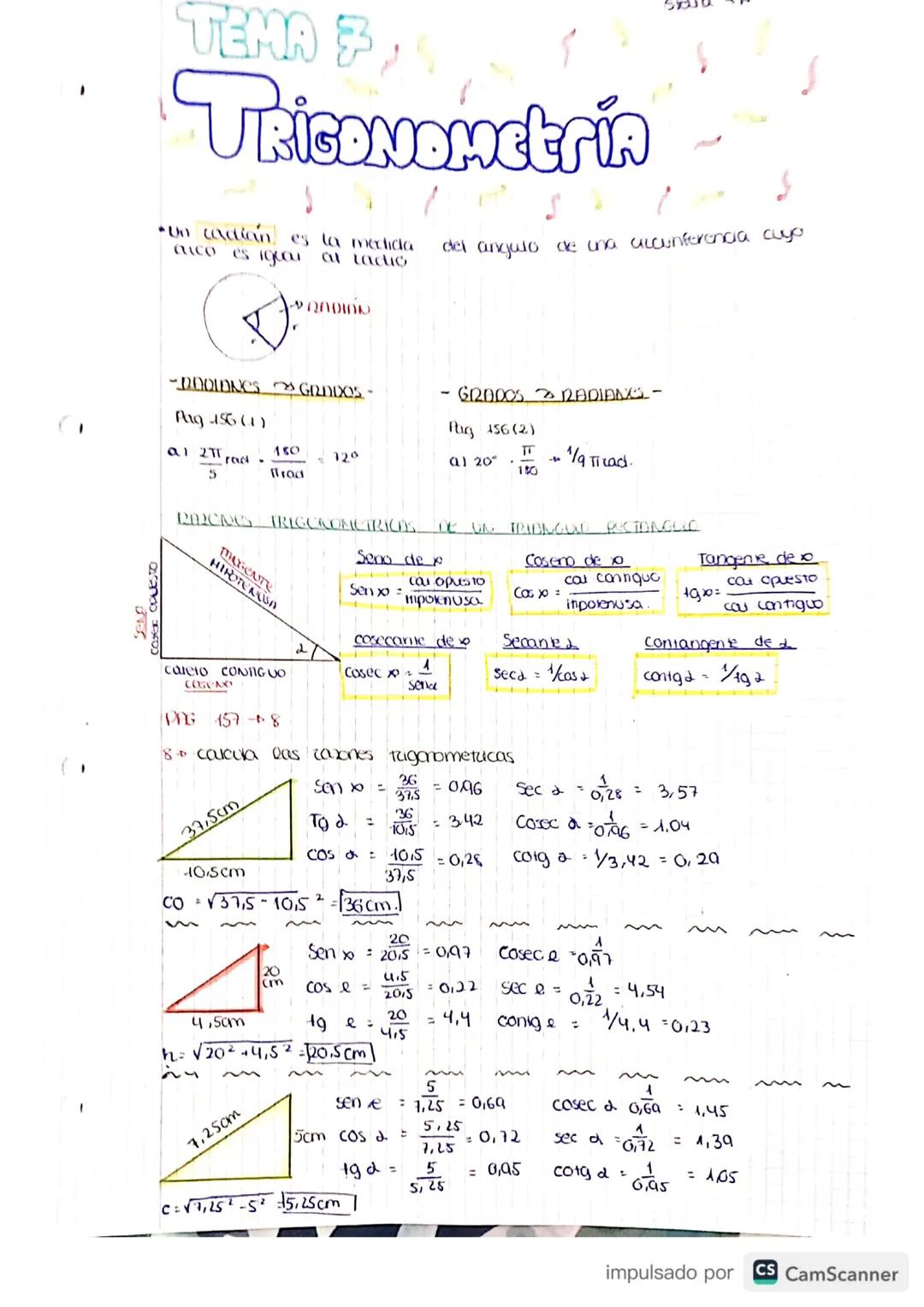
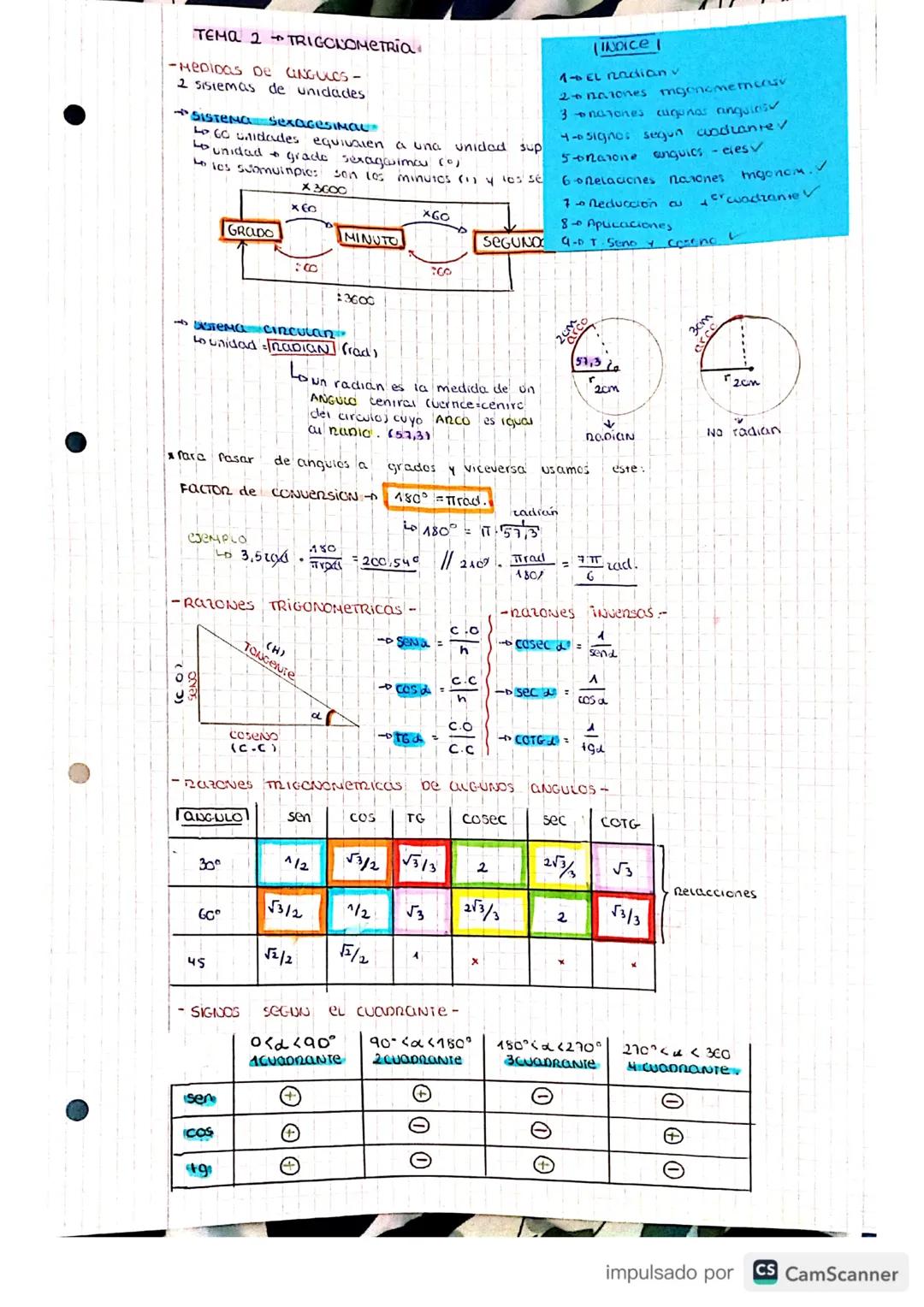
Un radián es simplemente la medida de un ángulo donde el arco es igual al radio del círculo. Es otra forma de medir ángulos, como los grados pero más "matemática".
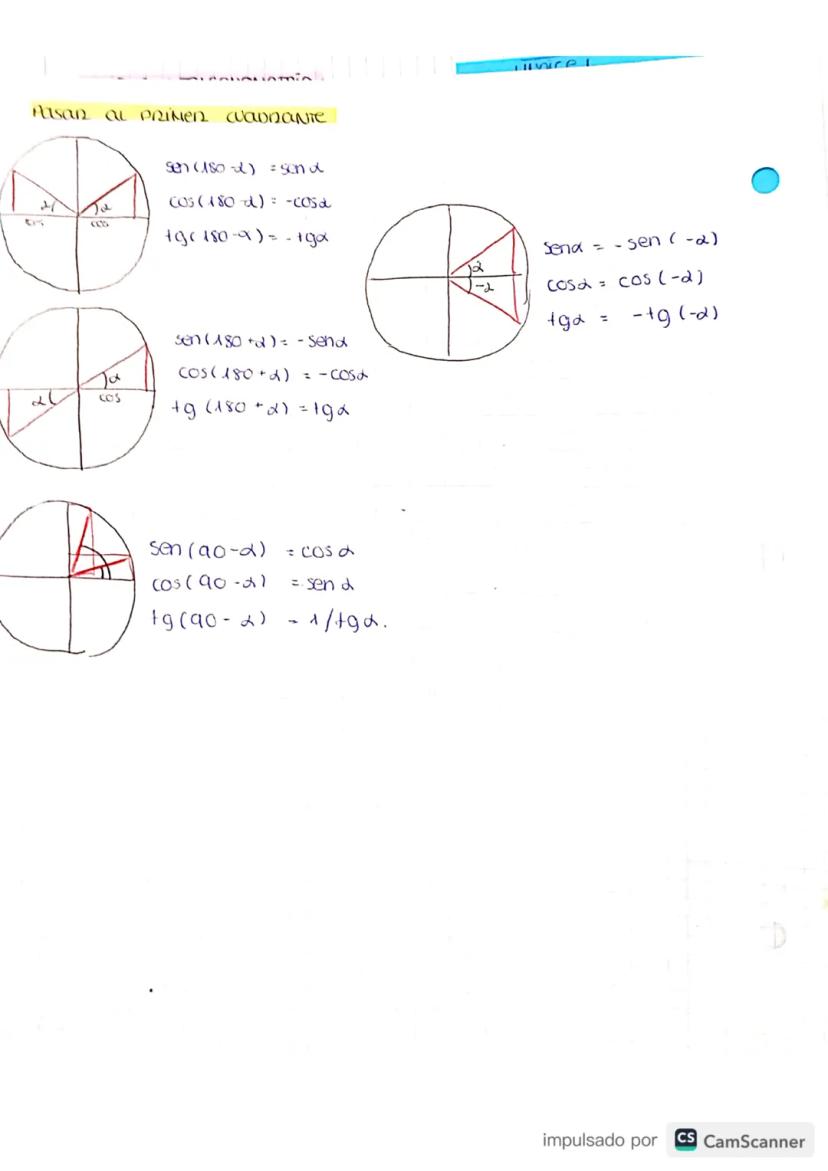
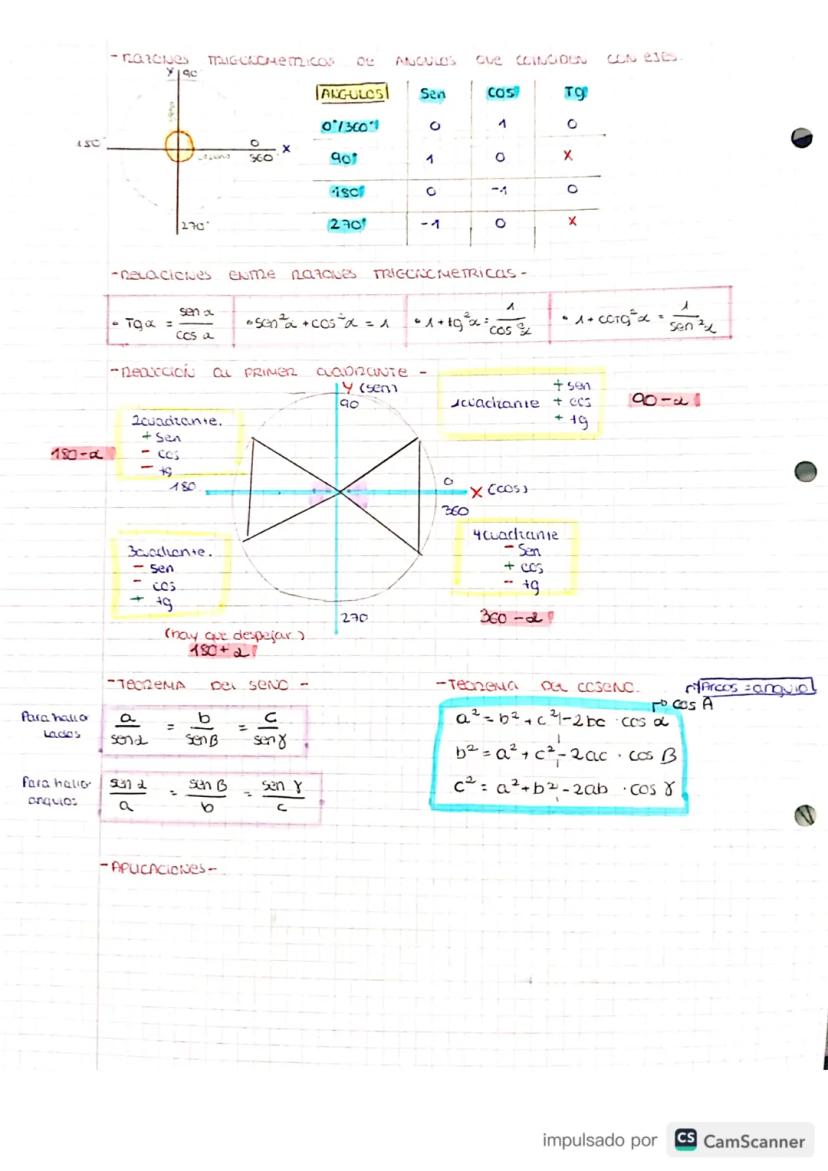
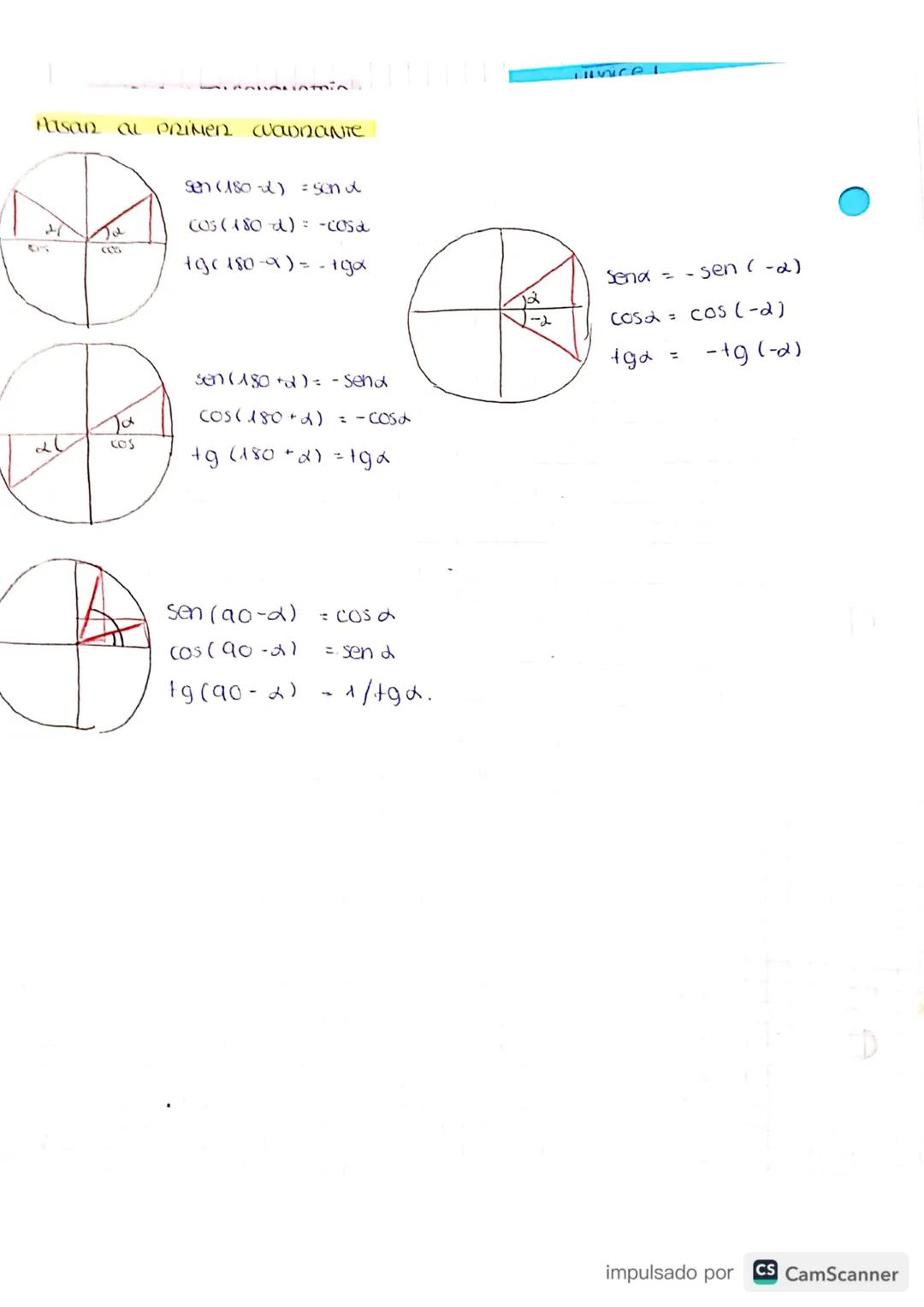
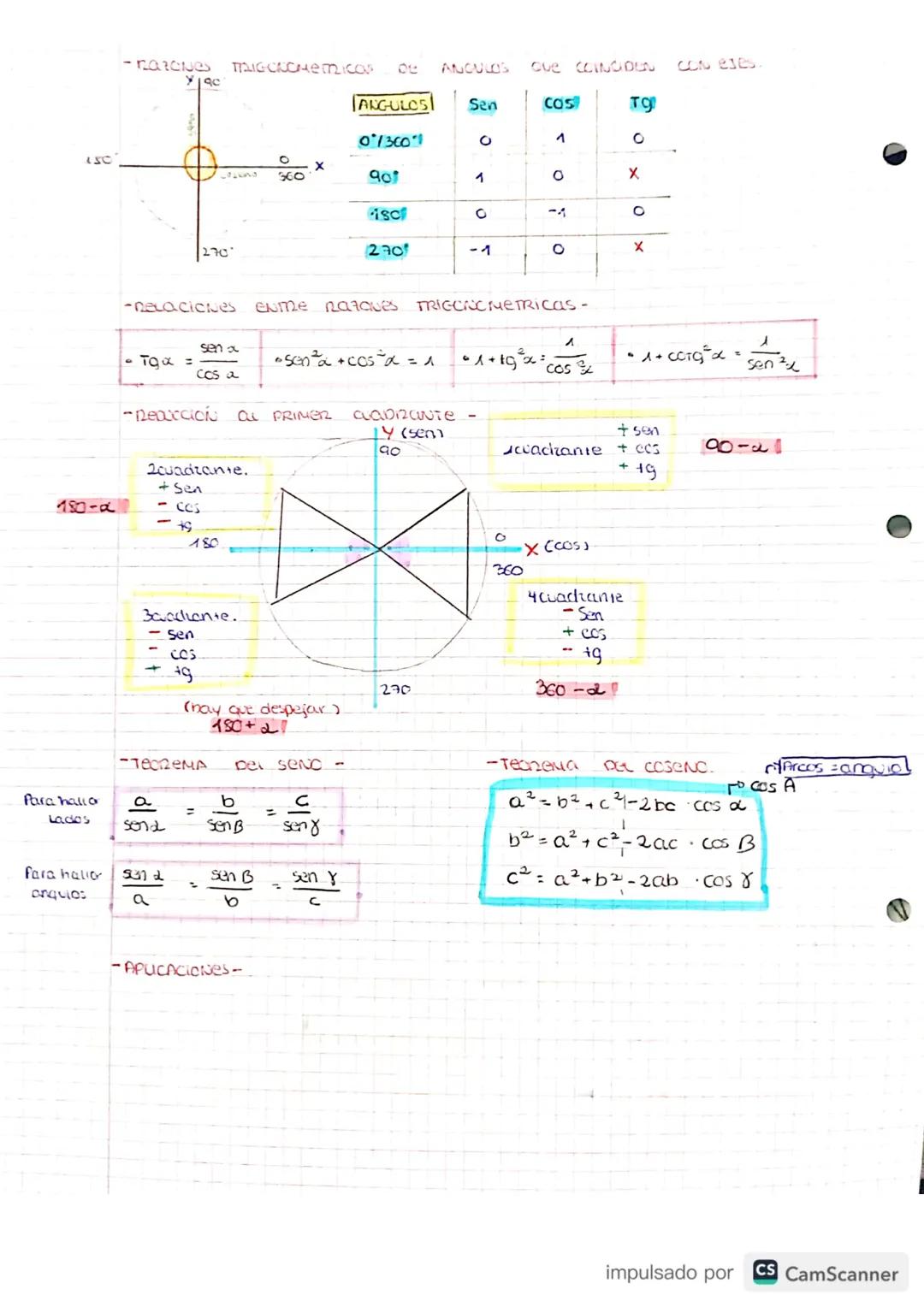
Para convertir entre grados y radianes, usa estas fórmulas clave: 180° = π rad. Por ejemplo, 20° = π/9 rad, y 2π rad = 360°.
Las razones trigonométricas básicas en un triángulo rectángulo son: seno α = cateto opuesto/hipotenusa, coseno α = cateto adyacente/hipotenusa, y tangente α = cateto opuesto/cateto adyacente.
También tienes las razones inversas: cosecante α = 1/sen α, secante α = 1/cos α, y cotangente α = 1/tg α. Estas aparecen mucho en los ejercicios, así que memorizarlas te ahorrará tiempo.
💡 Truco: Para recordar seno, coseno y tangente, usa "SOH-CAH-TOA" Seno=Opuesto/Hipotenusa,Coseno=Adyacente/Hipotenusa,Tangente=Opuesto/Adyacente