Elementos básicos para el análisis de funciones

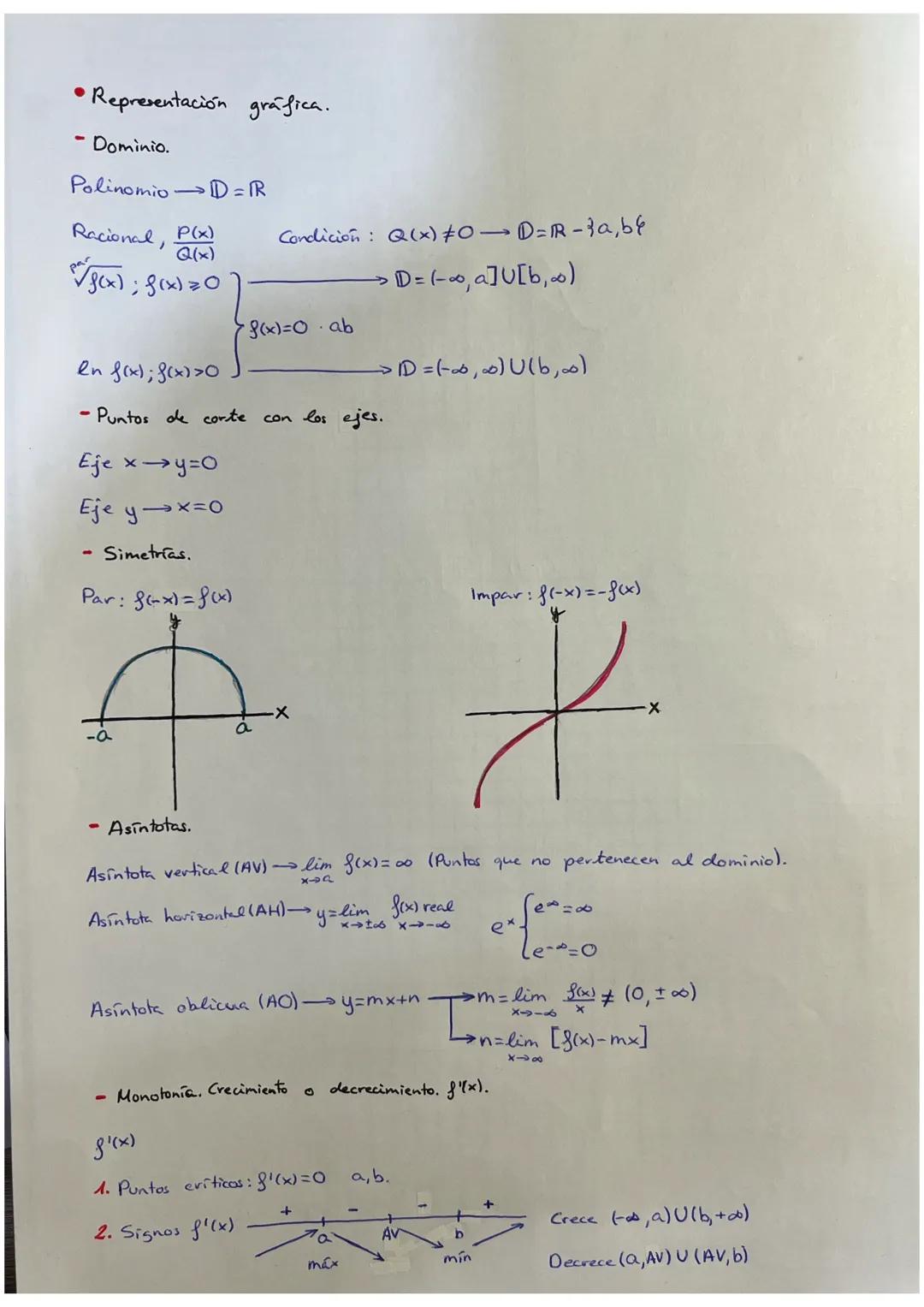
Analizar una función gráficamente requiere varios pasos fundamentales. Empezamos siempre por el dominio: para funciones polinómicas es todo ℝ, para funciones racionales P(x)/Q(x) excluimos donde Q(x)=0, y para radicales √f(x) necesitamos que f(x)≥0.

Los puntos de corte son súper fáciles de encontrar. Con el eje y: sustituyes x=0 en la función. Con el eje x: haces f(x)=0 y resuelves la ecuación.

Para las simetrías, solo tienes que comprobar dos casos: si f$-x$=f(x) es par (simétrica respecto al eje y), si f$-x$=-f(x) es impar (simétrica respecto al origen).

¡Dato clave! Las asíntotas aparecen en los puntos problemáticos del dominio y en el infinito.

Las asíntotas verticales están donde el límite tiende a ±∞ (puntos fuera del dominio). Las horizontales cuando el límite en ±∞ es un número real. Las oblicuas y=mx+n aparecen cuando m=lim$f(x)/x$ es finito y distinto de 0, y n=lim$f(x)-mx$.

Para estudiar el crecimiento, calculas f'(x), encuentras los puntos críticos $donde f'(x)=0$, y estudias el signo de la derivada en cada intervalo.

Concavidad y curvatura de funciones

El estudio de la concavidad te dice hacia dónde se curva tu función, y es más simple de lo que parece. Usas la segunda derivada f''(x) para determinar la forma de la curva en cada zona.

El proceso es idéntico al del crecimiento: primero encuentras donde f''(x)=0, luego estudias el signo de f''(x) en cada intervalo. Donde f''(x)>0 la función es cóncava hacia arriba (forma de U), donde f''(x)<0 es cóncava hacia abajo (forma de ∩).

Los puntos de inflexión aparecen donde cambia la concavidad, es decir, donde f''(x)=0 y hay cambio de signo. En estos puntos la función "cambia de curvatura".

¡Truco de experto! Si dominas el análisis del signo de las derivadas, ya tienes controlado todo el comportamiento de la función.

Con estos elementos ya puedes hacer una representación gráfica completa: dominio, cortes, simetrías, asíntotas, crecimiento y concavidad. ¡Es solo cuestión de práctica!