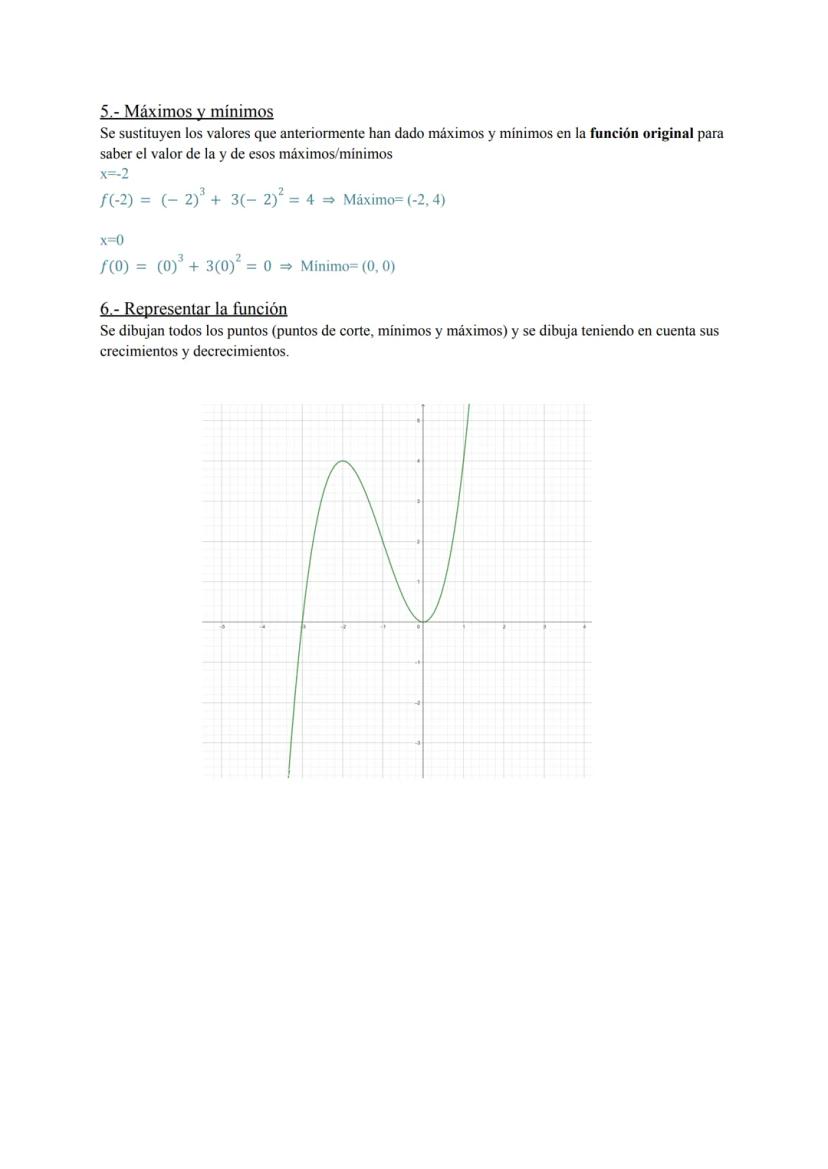
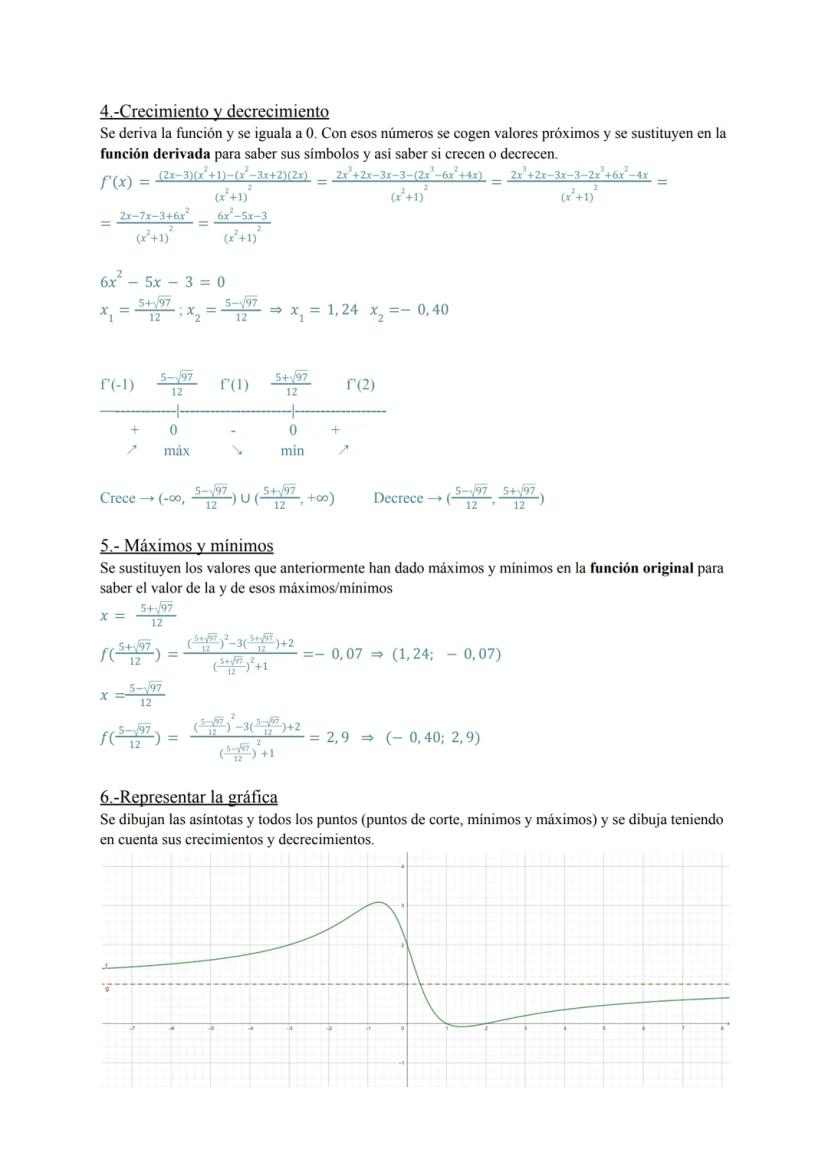
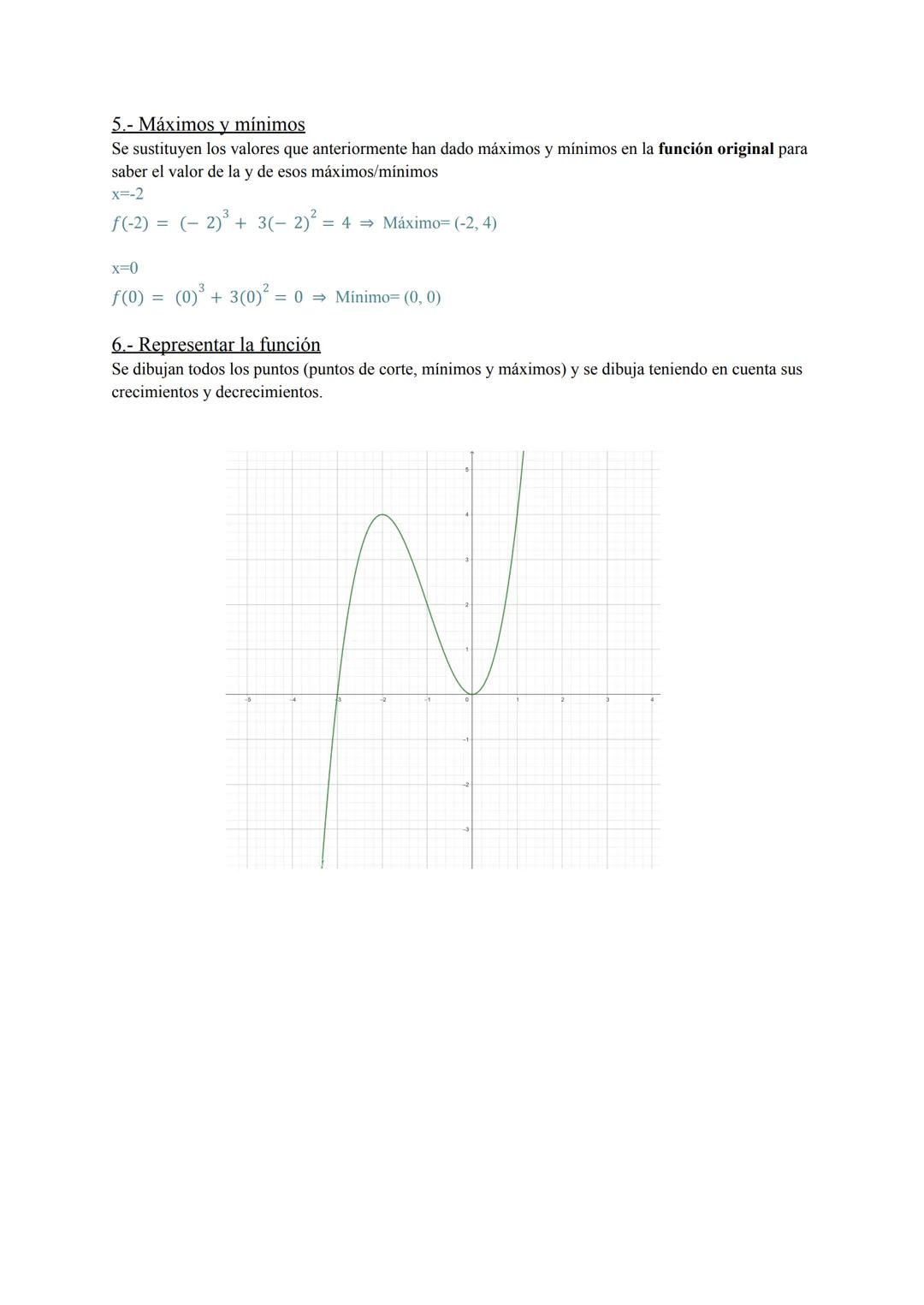
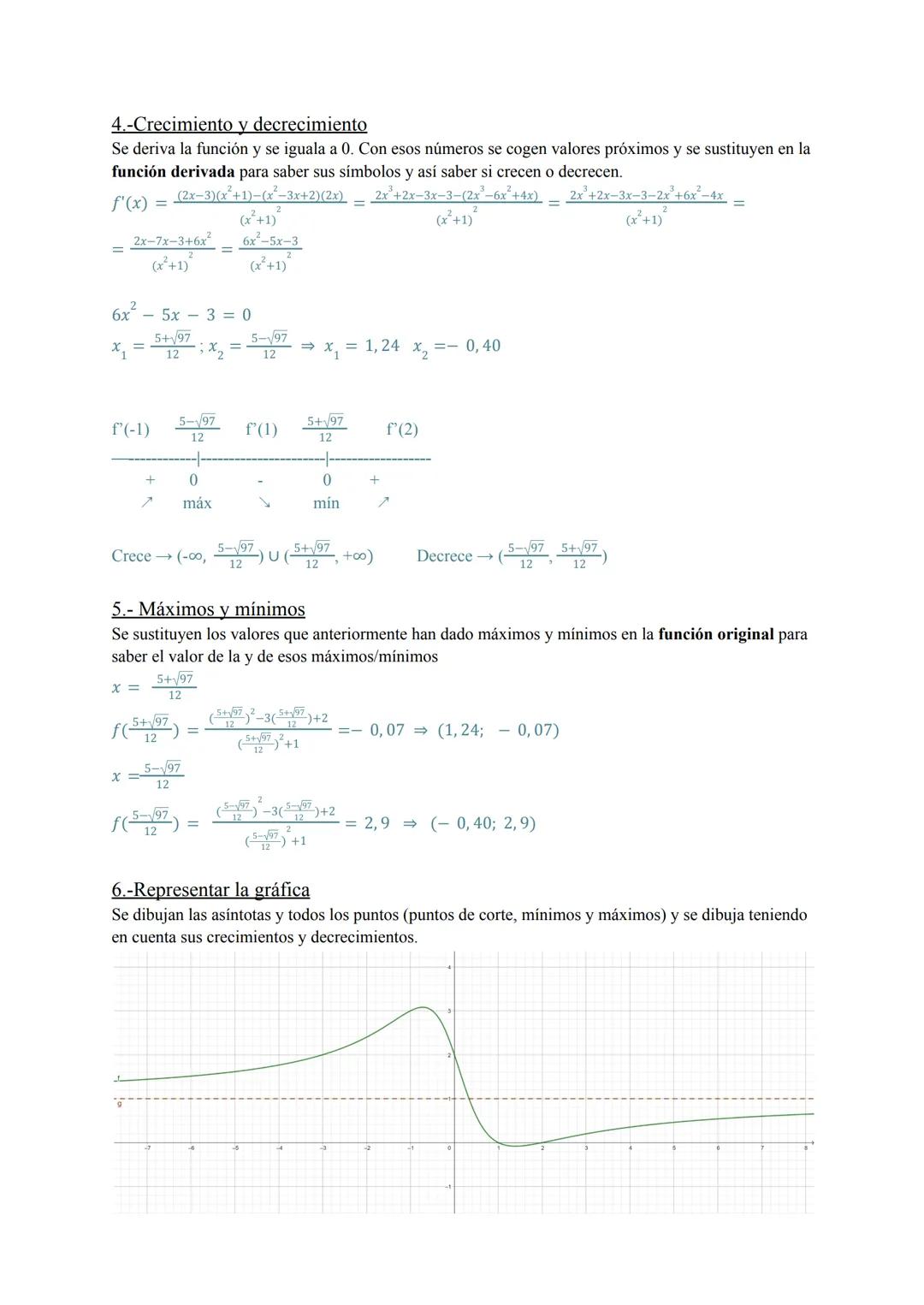
Análisis completo de funciones racionales

¿Sabías que las funciones racionales aparecen constantemente en física y economía? Vamos a ver cómo analizar paso a paso la función $f(x) = \frac{x^2 - 3x + 2}{x + 1}$.

El dominio es súper fácil de calcular: solo tienes que encontrar dónde el denominador se hace cero. En este caso, $x + 1 = 0$, así que $x = -1$. Por tanto, el dominio son todos los números reales excepto $x = -1$.

Para los puntos de corte, hay dos pasos simples. Con el eje X: igualas la función a cero, lo que significa que el numerador debe ser cero: $x^2 - 3x + 2 = 0$. Resolviendo obtienes $x = 1$ y $x = 2$, dando los puntos $(1,0)$ y $(2,0)$. Con el eje Y: sustituyes $x = 0$ en la función: $f(0) = \frac{2}{1} = 2$, así que el punto es $(0,2)$.

Las asíntotas determinan cómo se comporta la función en los extremos. La asíntota vertical aparece en $x = -1$ (donde no existe la función). Para la horizontal, como el numerador y denominador tienen el mismo grado, divides los coeficientes principales: $\frac{1}{1} = 1$, por lo que $y = 1$ es asíntota horizontal.

Truco: Si hay asíntota horizontal, nunca habrá asíntota oblicua. ¡Es una regla que te ahorrará tiempo!