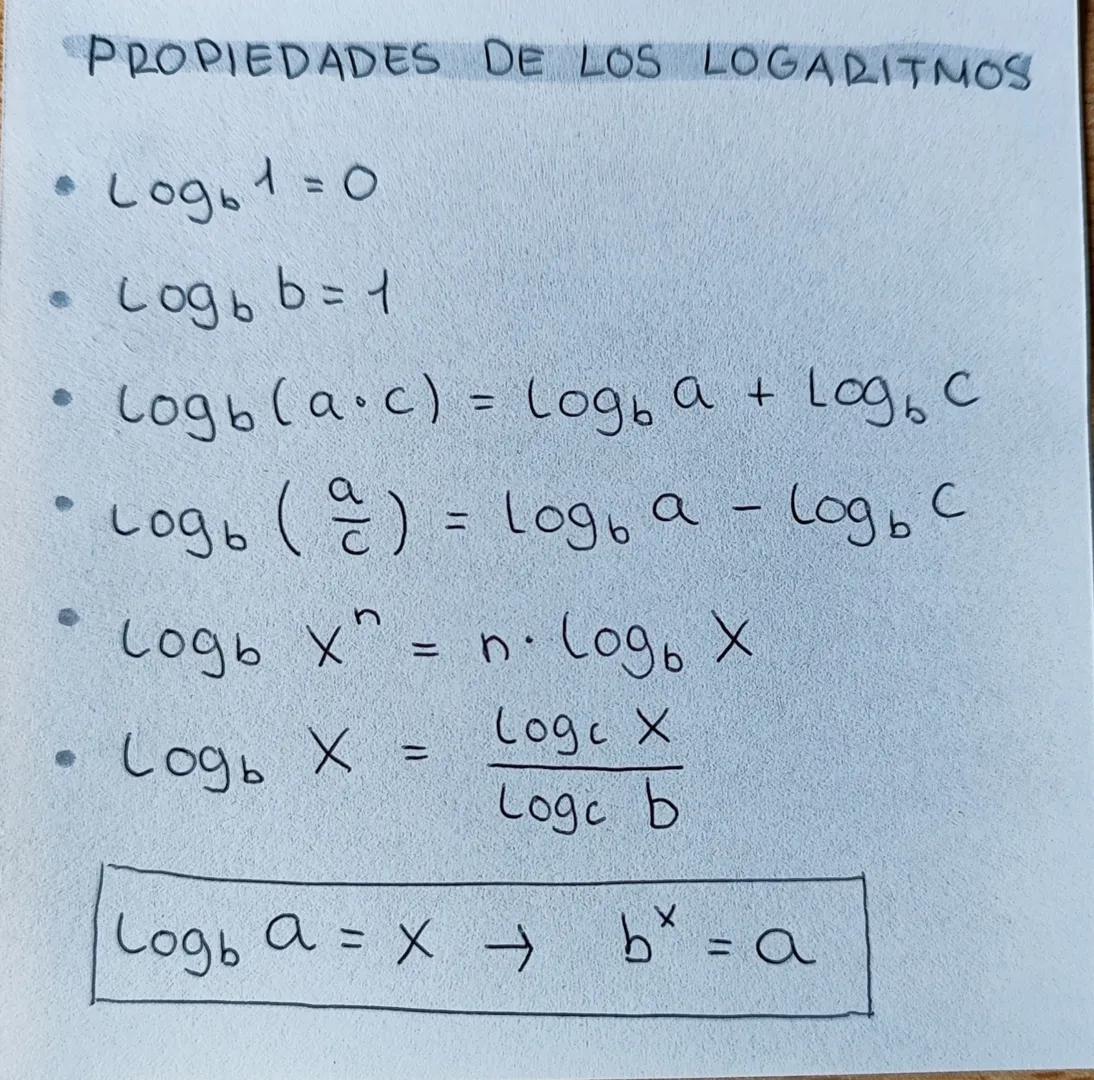
Propiedades de los Logaritmos

¿Alguna vez te has sentido confundido con los logaritmos? No te preocupes, estas propiedades te harán la vida más fácil. Lo primero que debes recordar es que un logaritmo en base b de un número es el exponente al que hay que elevar b para obtener dicho número.

Las propiedades fundamentales son sencillas. El logaritmo en base b de 1 siempre es 0 (porque b⁰ = 1). Y el logaritmo en base b de b es siempre 1 (porque b¹ = b). Estas son tus reglas base para empezar.

Para operaciones más complejas, recuerda que el logaritmo de un producto es la suma de logaritmos (log₍ₐ·c) = log₍a + log₍c), mientras que el logaritmo de una división es la resta de logaritmos (log₍(a/c) = log₍a - log₍c). Cuando tengas potencias, el logaritmo de x elevado a n es igual a n por el logaritmo de x (log₍x^n = n · log₍x).

💡 Truco para recordar: Las operaciones de multiplicación y división "dentro" del logaritmo se convierten en sumas y restas "fuera" del logaritmo. Esto convierte operaciones complicadas en otras más sencillas.

Finalmente, si necesitas cambiar de base, usa la fórmula log₍x = (log₍x)/(log₍b). Y recuerda la relación fundamental: si log₍a = x, entonces b^x = a. Esta última propiedad es la definición misma del logaritmo y te permite "despejar" cuando el logaritmo aparece en ecuaciones.