Operaciones y Aplicaciones con Fracciones Algebraicas
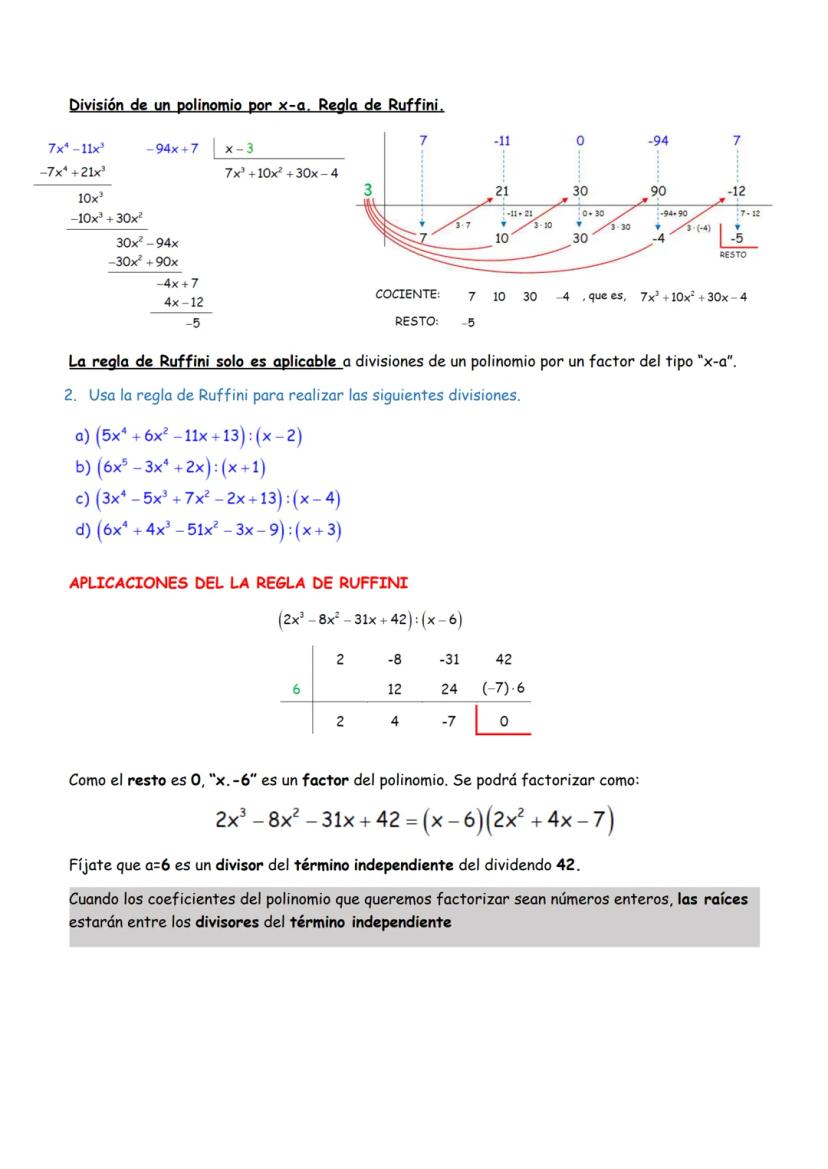
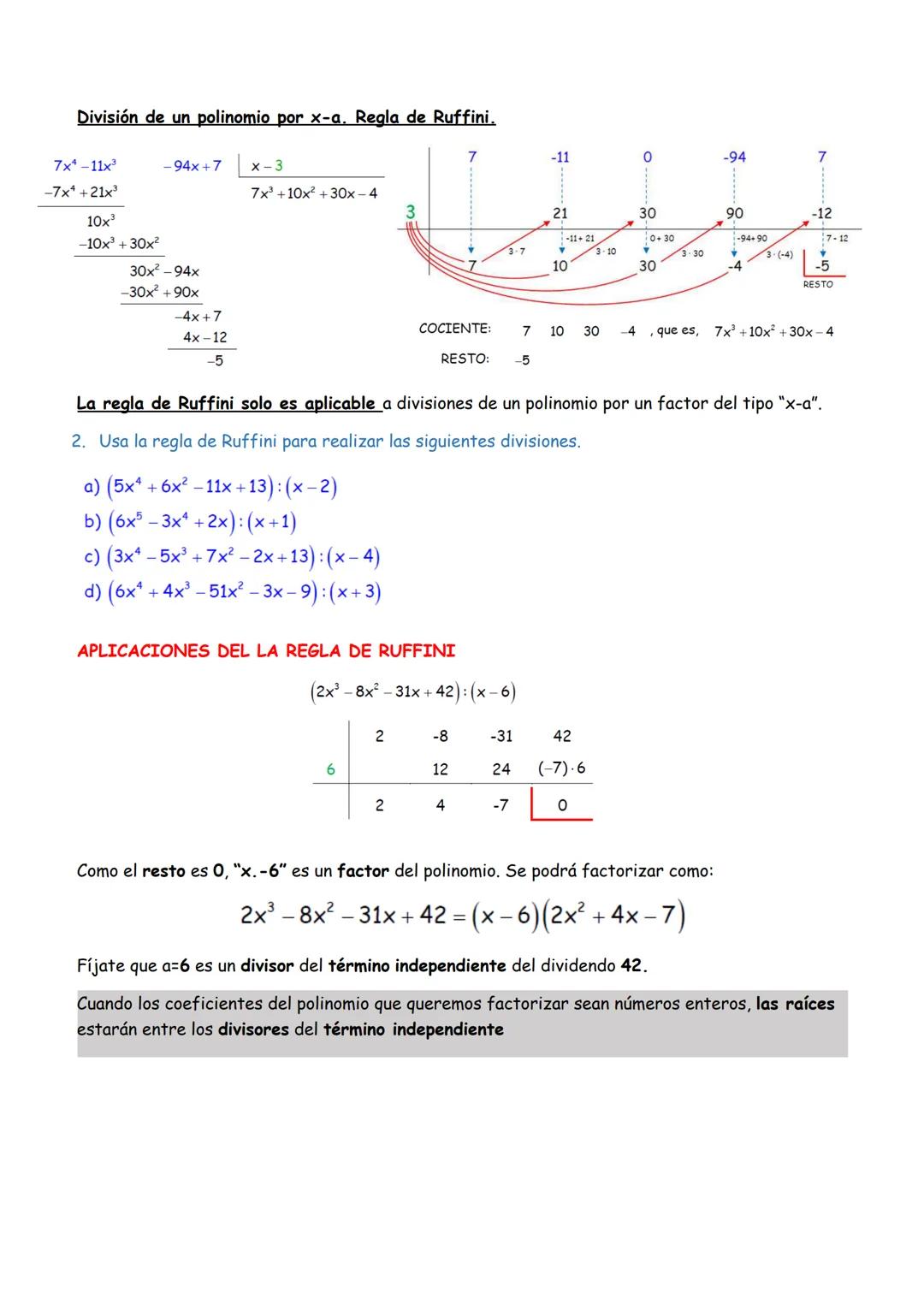
Las operaciones combinadas requieren seguir el orden correcto: paréntesis, multiplicaciones y divisiones (de izquierda a derecha), luego sumas y restas. Mantén siempre factorizado para simplificar en cada paso.
Las fracciones algebraicas aparecen en problemas de la vida real: velocidades, concentraciones, tiempos de trabajo conjunto. La clave es traducir correctamente el enunciado al lenguaje algebraico.
Por ejemplo, si un grifo llena un tanque en x minutos, llena 1/x del tanque por minuto. Si dos grifos trabajan juntos, sus velocidades se suman: x1+y1 del tanque por minuto.
💡 Aplicación real: Las fracciones algebraicas son fundamentales en física velocidad=distancia/tiempo y economía preciopromedio=costetotal/cantidad.