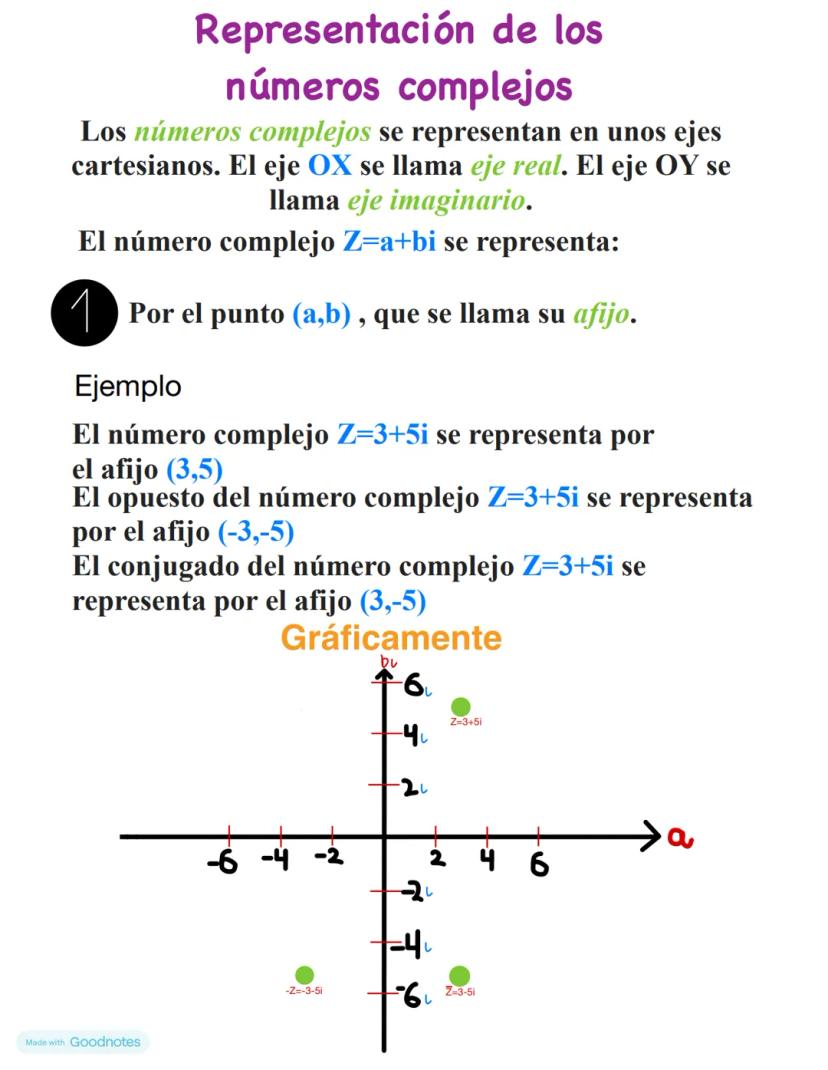
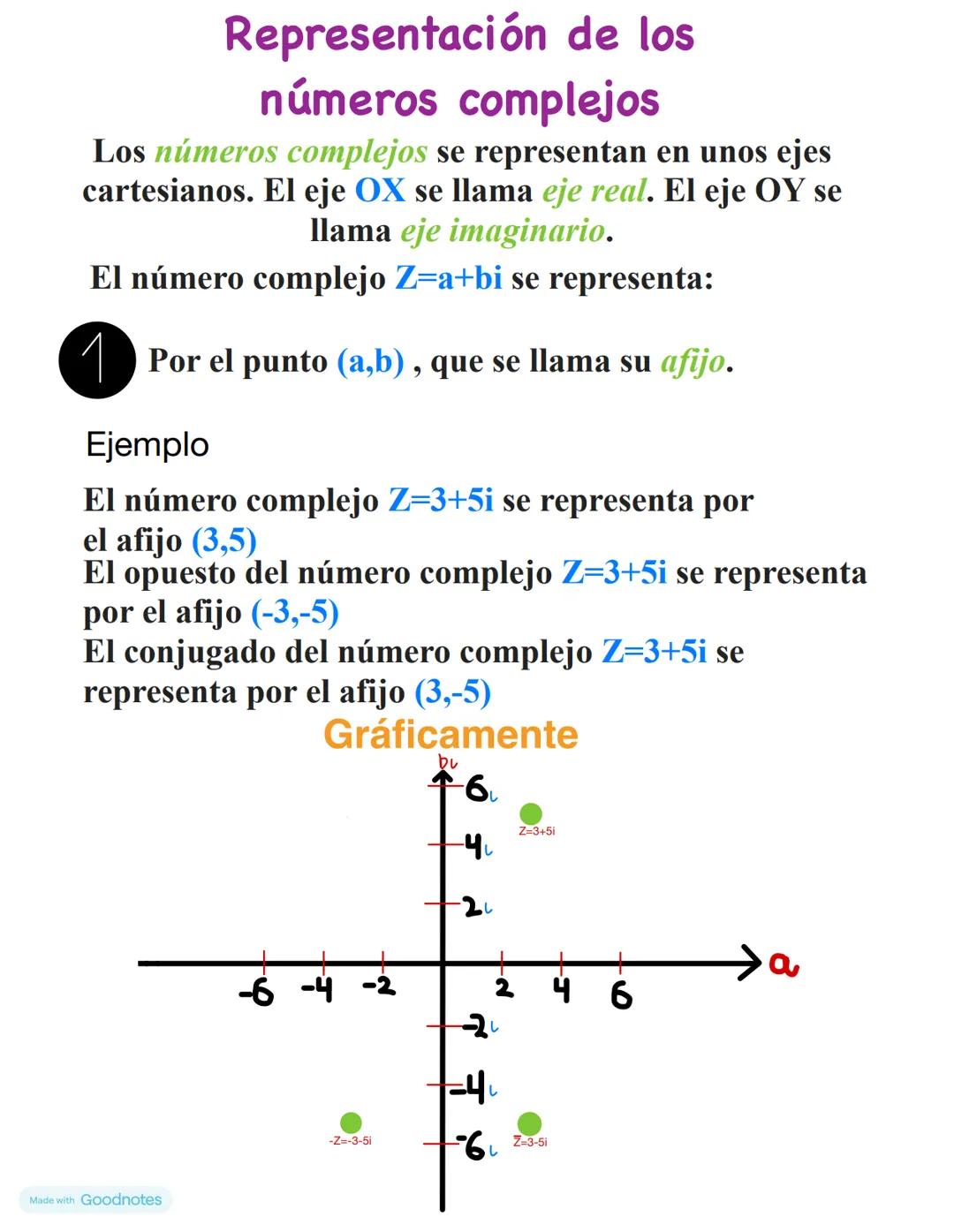
Potencias de la unidad imaginaria
Calcular potencias de i es más fácil de lo que parece porque siguen un patrón que se repite cada 4 potencias. Observa: i⁰ = 1, i¹ = i, i² = -1, i³ = -i, y i⁴ = 1 otra vez.
Para calcular cualquier potencia como i²², solo necesitas dividir el exponente entre 4 y fijarte en el resto. Si 22 ÷ 4 = 5 con resto 2, entonces i²² = i² = -1.
Este truco funciona siempre: i²⁷ tiene resto 3 al dividir entre 4, así que i²⁷ = i³ = -i. Es como un ciclo que nunca se rompe.
💡 Método infalible: Divide el exponente entre 4, mira el resto, y usa i⁰ = 1, i¹ = i, i² = -1, i³ = -i.