Continuidad y Discontinuidades
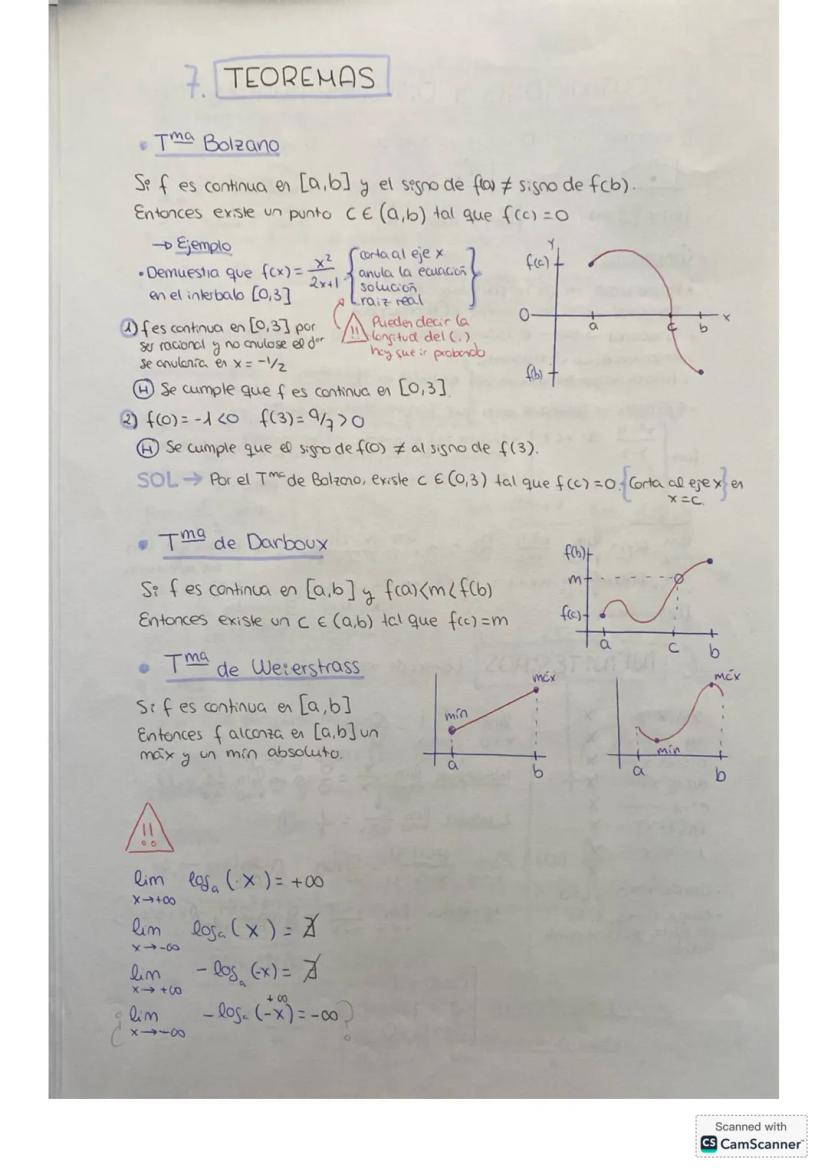
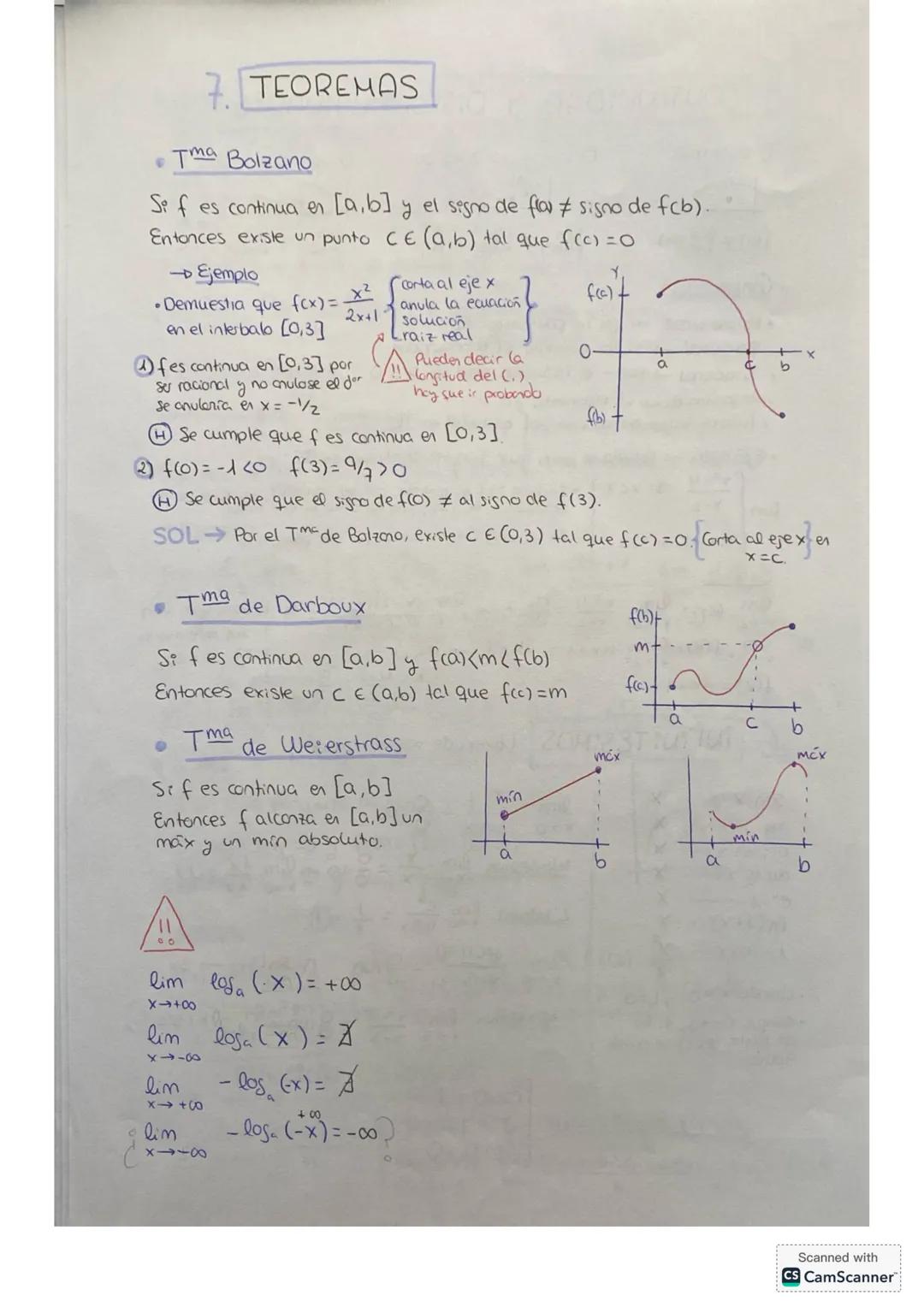
Una función es continua cuando puedes dibujarla sin levantar el lápiz del papel. Matemáticamente, necesitas que el límite coincida con el valor de la función en ese punto.
Existen tres tipos de discontinuidades: evitable (cuando el límite existe pero no coincide con f(a)), salto infinito (el límite es infinito), y salto finito (los límites laterales son diferentes pero finitos).
Los infinitésimos equivalentes son tu mejor herramienta para límites cuando x→0: sen x ~ x, tg x ~ x, e^x - 1 ~ x, ln1+x ~ x, y 1 - cos x ~ x²/2. ¡Son súper útiles!
💡 Dato importante: Las funciones polinómicas son continuas en todos los reales, las racionales donde no se anula el denominador.