Conjuntos Numéricos y Números Reales
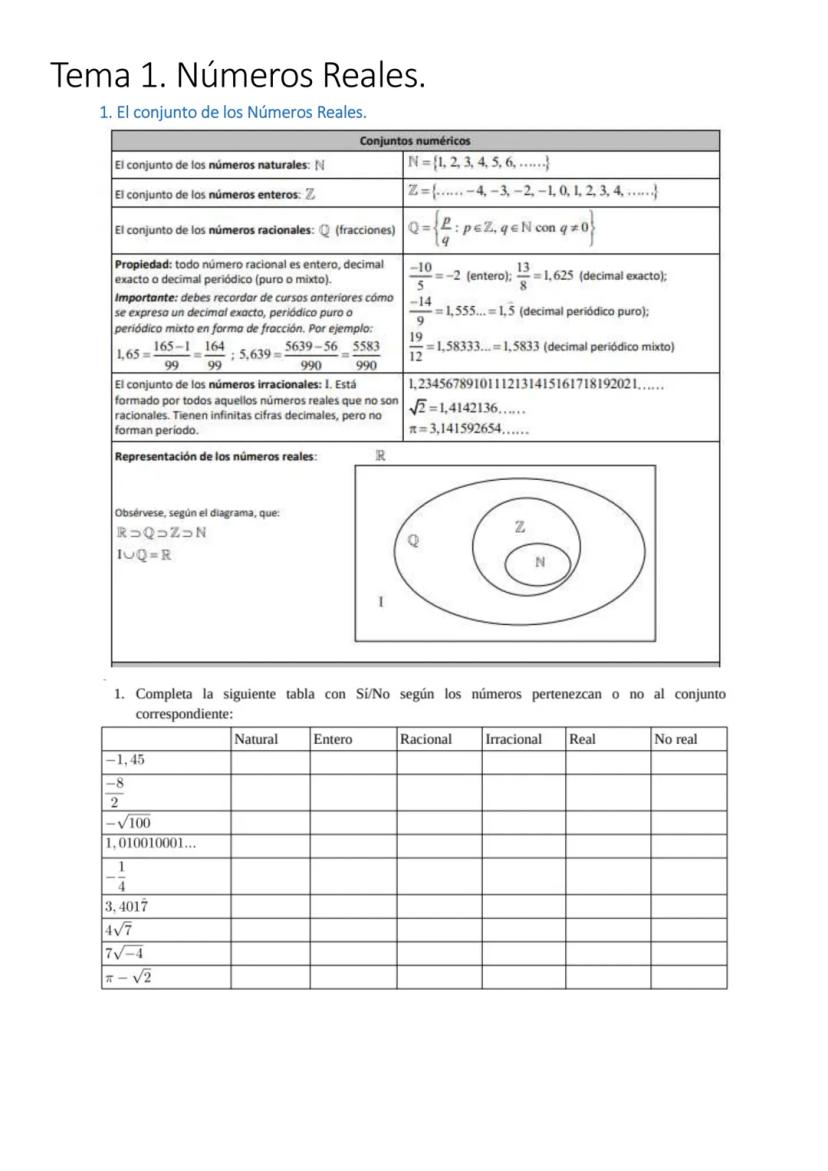
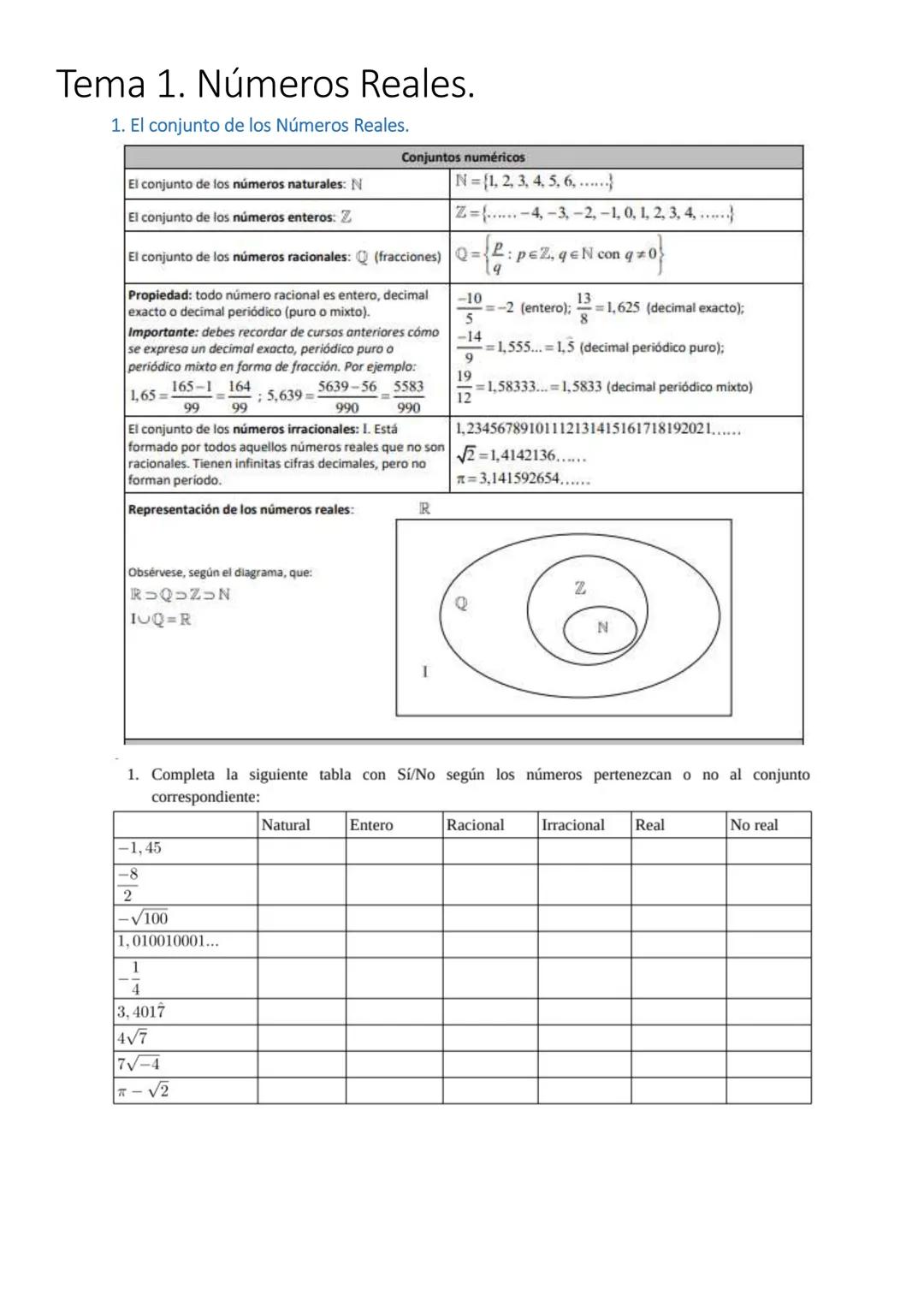
Los números reales incluyen todos los números que conoces y algunos más. Empecemos por lo básico: los naturales N = {1, 2, 3, 4...} son los que usas para contar, y los enteros Z incluyen también los negativos y el cero.
Los números racionales Q son todas las fracciones p/q donde p es entero y q es natural (q ≠ 0). Lo genial es que todo número racional se puede escribir como decimal exacto (como 0,25) o periódico como0,333...=0,3ˉ.
Por otro lado, los números irracionales I tienen infinitas cifras decimales sin patrón. Piensa en √2 = 1,4142136... o π = 3,141592654... - nunca terminan ni se repiten.
¡Ojo! Los números reales R incluyen tanto racionales como irracionales. Es como si fuera toda la recta numérica completa.