Conjuntos y Números Reales

Los conjuntos numéricos son la base de todo lo que viene después. Piensa en ellos como familias organizadas: naturales (N), enteros (Z), racionales (Q) e irracionales, que juntos forman los números reales (IR).

Las operaciones entre conjuntos son súper útiles para resolver problemas. La unión (A∪B) junta todos los elementos, mientras que la intersección (A∩B) solo incluye los elementos comunes. La diferencia $A-B$ te da los elementos que están en A pero no en B.

El valor absoluto siempre te da un resultado positivo o cero. Recuerda: |x| = x si x≥0, y |x| = -x si x<0. Los intervalos son formas elegantes de expresar rangos de números: usa corchetes [ ] para incluir el extremo y paréntesis ( ) para excluirlo.

¡Truco! Para recordar los intervalos: los corchetes "abrazan" el número (lo incluyen), los paréntesis lo "rechazan" (no lo incluyen).

Ejercicios Prácticos de Intervalos y Valor Absoluto

Cuando resuelves ecuaciones con valor absoluto, recuerda que |x| = a tiene dos soluciones: x = a y x = -a. Es como preguntarse: ¿qué números están a una distancia 'a' del cero?

Para desigualdades con valor absoluto, |x| ≤ a significa que x está entre -a y a (intervalo cerrado). Pero |x| > a significa que x está fuera de ese rango, creando dos intervalos separados.

Los ejercicios muestran patrones claros: |x-4| ≤ 2 se convierte en -2 ≤ x-4 ≤ 2, lo que da [2,6]. Siempre suma o resta el mismo número a toda la desigualdad para despejar x.

¡Cuidado! Cuando |x-4| > 2, la solución son DOS intervalos: (-∞, 2) ∪ (6, ∞). No olvides la unión.

Logaritmos: Propiedades y Aplicaciones

Los logaritmos son simplemente otra forma de escribir exponentes. Si log_a P = x, entonces a^x = P. Es como preguntarse: ¿a qué potencia debo elevar 'a' para obtener P?

Las propiedades de los logaritmos son tu mejor herramienta:

• log(A·B) = log A + log B (el producto se vuelve suma)
• log$A/B$ = log A - log B (la división se vuelve resta)
• log$A^n$ = n·log A (el exponente sale multiplicando)

El logaritmo neperiano (ln) usa base e y aparece constantemente en cálculo. Para cambiar de base, usa la fórmula: log_a P = log P / log a.

¡Estrategia! En los ejercicios, sustituye los valores dados directamente en las fórmulas. No intentes memorizar resultados específicos.

Polinomios: Factorización y Raíces

Factorizar polinomios es como desarmar un rompecabezas para ver sus piezas básicas. Siempre empieza sacando factor común (como x³ en el ejemplo).

La regla de Ruffini es tu mejor amiga para encontrar raíces. Prueba con divisores del término independiente: ±1, ±2, ±3, etc. Cuando encuentres una raíz, puedes dividir el polinomio y reducir su grado.

Para polinomios de grado 2, usa la fórmula cuadrática: x = $-b ± √(b²-4ac)$ / 2a. Si el discriminante es negativo, no hay raíces reales.

¡Tip de oro! Si un polinomio no tiene raíces racionales obvias, puede que tengas raíces fraccionarias. Prueba con p/q donde p divide al término independiente y q al coeficiente principal.

Fracciones Algebraicas y Ecuaciones Especiales

Las fracciones algebraicas se simplifican factorizando numerador y denominador, luego cancelando factores comunes. Es fundamental factorizar completamente antes de simplificar.

Para sumar fracciones algebraicas, encuentra el mínimo común múltiplo de los denominadores. Multiplica cada fracción por lo que le falta para tener ese denominador común.

Las ecuaciones bicuadradas $tipo x⁴ - 10x² + 9 = 0$ se resuelven con el cambio t = x². Resuelves la ecuación cuadrática en t, luego encuentras x = ±√t.

En ecuaciones con fracciones, multiplica toda la ecuación por el denominador común para eliminar las fracciones. ¡Pero cuidado con las restricciones del dominio!

¡Importante! Siempre verifica que tus soluciones no anulen ningún denominador de la ecuación original.

Ecuaciones Exponenciales y Logarítmicas

Las ecuaciones exponenciales se resuelven igualando las bases cuando es posible. Si 2^$x²-4x$ = 1/16, reescribe como 2^$x²-4x$ = 2^(-4), entonces x²-4x = -4.

Cuando las bases no se pueden igualar, usa logaritmos: toma ln o log en ambos lados. Por ejemplo, 5^$x²-1$ = 7 se vuelve $x²-1$·ln 5 = ln 7.

Para ecuaciones logarítmicas, usa las propiedades para simplificar. Si log x - log 4 = 2, entonces log$x/4$ = log(10²), por lo que x/4 = 100.

¡Truco! En ecuaciones exponenciales complicadas, intenta sacar factor común. En 3^$x+2$ - 3^x = 72, factoriza: 3^x(3² - 1) = 72.

Sistemas de Ecuaciones e Inecuaciones

Los sistemas no lineales requieren creatividad. Con raíces cuadradas, eleva al cuadrado ambos lados (pero verifica las soluciones). Con fracciones, multiplica por el denominador común.

Para sistemas con logaritmos y exponenciales, usa las propiedades para simplificar. Convierte productos en sumas y potencias en productos con coeficientes.

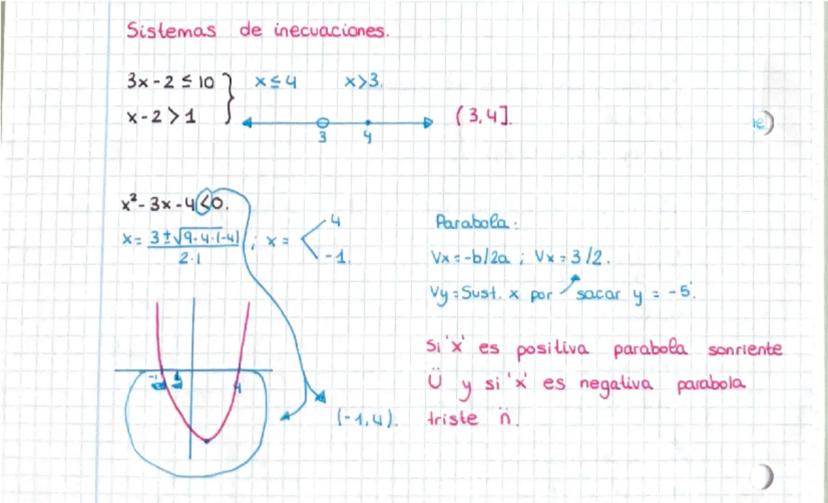
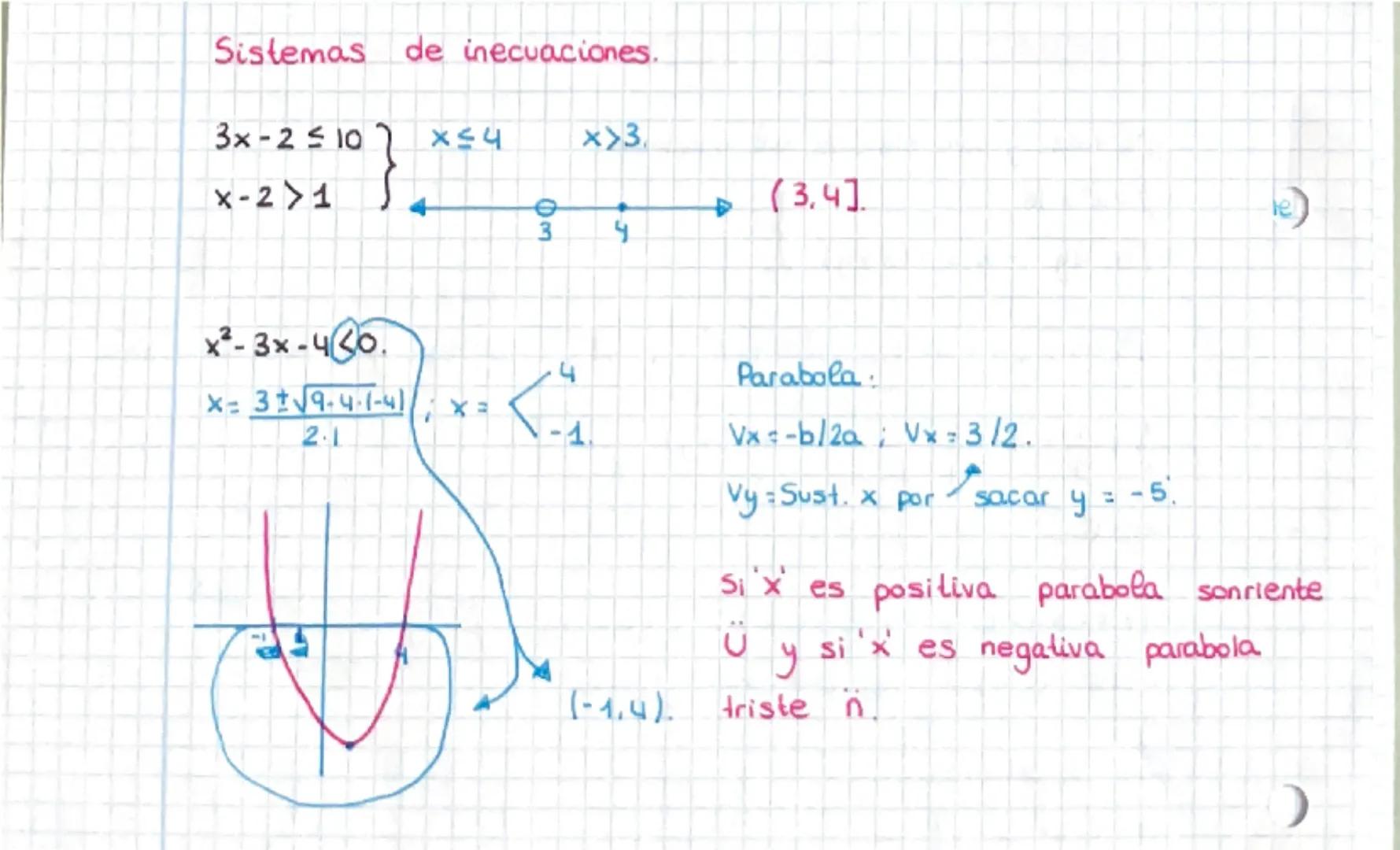
Las inecuaciones se resuelven como ecuaciones, pero cambia el sentido de la desigualdad cuando multiplicas o divides por un número negativo.

Para inecuaciones cuadráticas, factoriza y usa una tabla de signos. La parábola te ayuda a visualizar dónde es positiva o negativa.

¡Clave! En sistemas complicados, despeja una variable en la ecuación más simple y sustituye en las demás.

Sistemas de Inecuaciones y Representación Gráfica

Los sistemas de inecuaciones requieren que se cumplan todas las condiciones simultáneamente. La solución es la intersección de todas las soluciones individuales.

Para inecuaciones cuadráticas, encuentra las raíces y determina el signo de la parábola. Si el coeficiente de x² es positivo, la parábola "sonríe"; si es negativo, está "triste".

El vértice de la parábola está en x = -b/2a. Sustituye este valor para encontrar la coordenada y. Esto te ayuda a visualizar la función.

¡Visualiza! Dibuja siempre la parábola. Te ayudará a entender dónde la función es positiva o negativa.

Inecuaciones con Dos Incógnitas

Las inecuaciones lineales con dos variables dividen el plano en dos regiones. La recta es la frontera, y debes determinar qué lado satisface la desigualdad.

Para encontrar la región solución, elige un punto de prueba (como (0,0) si no está en la recta). Si satisface la desigualdad, toda esa región es solución.

Con sistemas de inecuaciones, la solución es la intersección de todas las regiones. Dibuja cada recta y sombrea gradualmente hasta encontrar la zona común.

¡Método! Siempre convierte la inecuación a la forma y ≥ f(x) o y ≤ f(x) para facilitar el trazado.

Sistemas de Tres Ecuaciones: Método de Gauss

El método de Gauss transforma el sistema en forma triangular. Elimina sistemáticamente variables hasta obtener una ecuación con una sola incógnita.

Empieza eliminando x de la segunda y tercera ecuaciones usando la primera. Luego elimina y de la tercera ecuación usando la segunda modificada.

Resuelve hacia atrás: encuentra z primero, luego sustituye para encontrar y, y finalmente encuentra x. Es como subir una escalera al revés.

¡Organización! Mantén los cálculos ordenados y verifica cada paso. Un error pequeño al principio se amplifica al final.