Fórmulas y Conceptos Básicos

Las matemáticas pueden parecer un rollo, pero en realidad son como un idioma que una vez que pillas la base, todo fluye mejor. Las fórmulas que ves como E=mc² o √$x+y²$ son solo formas de expresar relaciones entre números.

Piensa en las fórmulas como recetas de cocina: sigues los pasos y obtienes el resultado. Lo importante es entender qué significa cada símbolo y cómo se relaciona con los demás.

💡 Truco: Practica escribiendo las fórmulas a mano varias veces. Tu cerebro memoriza mejor cuando escribes físicamente.

Inecuaciones y Ecuaciones Exponenciales

Las inecuaciones son como ecuaciones, pero en lugar de buscar un valor exacto, buscas rangos de valores. Con las de primer grado es fácil: 3x ≥ -3 te da x ≥ -1, y listo.

Las ecuaciones exponenciales son más chungas al principio. El truco está en hacer sustituciones inteligentes: si tienes 3^x, lo cambias por t y trabajas con t. Luego vuelves atrás para encontrar x.

Para las ecuaciones logarítmicas, recuerda que log(a) = log(b) significa que a = b. Es tu herramienta más poderosa para resolver estos problemas.

💡 Clave: En exponenciales, busca siempre la misma base. En logarítmicas, usa las propiedades para simplificar antes de resolver.

Ecuaciones Irracionales y Sistemas

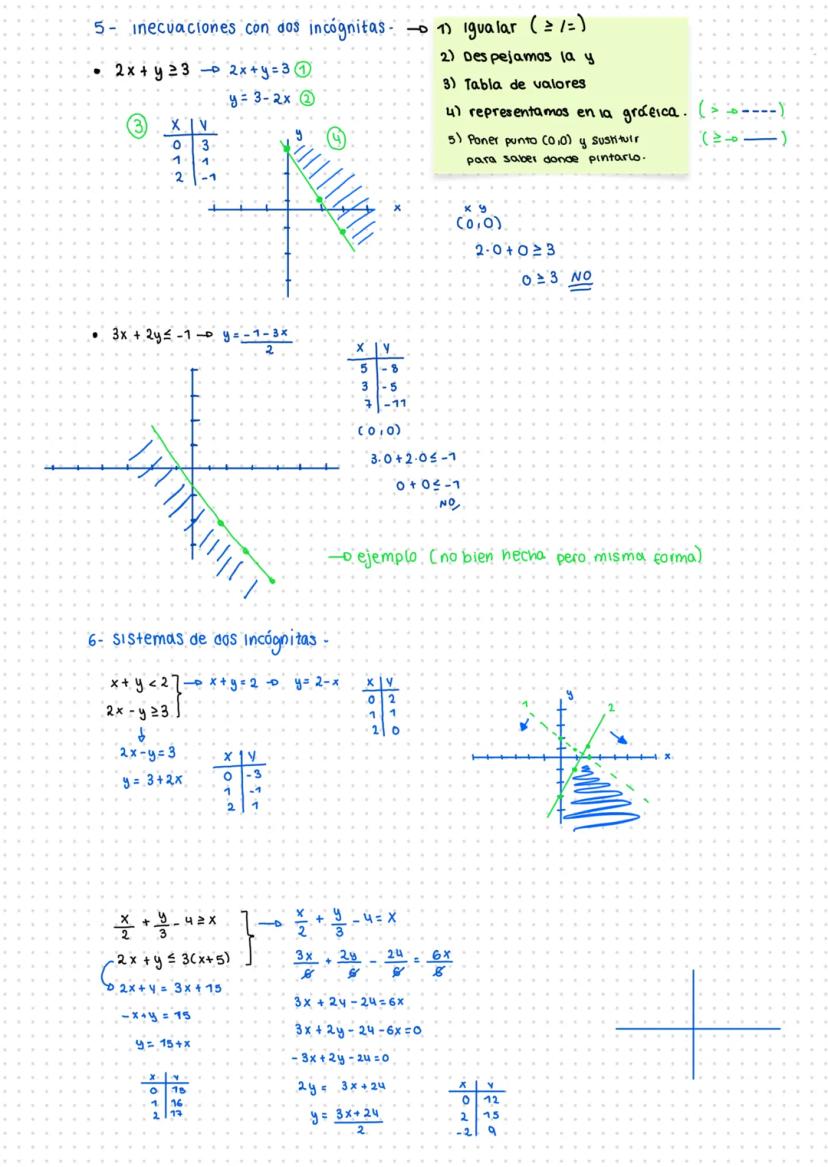
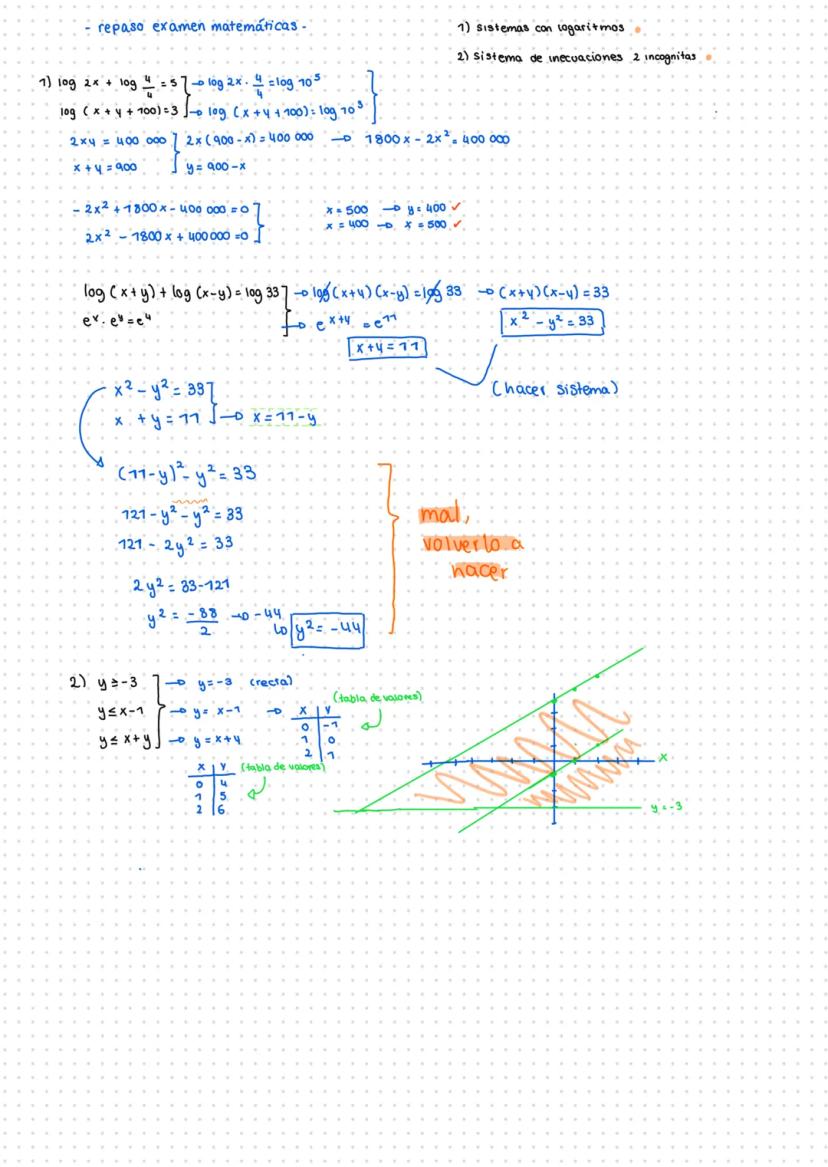
Con las ecuaciones irracionales (las que tienen raíces), el proceso es súper metódico: deja la raíz sola, eleva al cuadrado ambos lados, opera y ¡MUY IMPORTANTE! comprueba siempre el resultado.

Los sistemas de ecuaciones son como puzzles matemáticos. El método de Gauss es tu mejor amigo: combina las ecuaciones para eliminar variables paso a paso hasta que solo quede una.

En los problemas de alturas como el ejemplo, define bien tus variables desde el principio. x = altura de Luis, y = altura de Eusebio, z = altura de Pablo. Luego traduce el enunciado a ecuaciones.

💡 No olvides: En irracionales, SIEMPRE comprueba. Muchas soluciones que salen matemáticamente no son válidas en la ecuación original.

Ejercicios con Logaritmos y Sistemas Avanzados

Los logaritmos tienen propiedades que son oro puro: ln(a) + ln(b) = ln(a·b), y ln(a) - ln(b) = ln$a/b$. Úsalas para simplificar expresiones complicadas antes de resolver.

En el ejemplo del ejercicio 1, fíjate cómo se combinan todos los logaritmos en uno solo usando estas propiedades. Es como ordenar tu habitación: todo más claro y manejable.

Las ecuaciones fraccionarias requieren paciencia. Encuentra el mínimo común múltiplo, multiplica toda la ecuación por él, y las fracciones desaparecen como por arte de magia.

💡 Estrategia: Con logaritmos, simplifica primero usando propiedades. Con fracciones, elimínalas al principio multiplicando por el mcm.

Sistemas Logarítmicos e Inecuaciones Complejas

Los sistemas con logaritmos combinan lo mejor (y lo peor) de ambos mundos. Usa las propiedades de logaritmos para simplificar cada ecuación, luego aplica métodos de sistemas normales.

Las inecuaciones algebraicas necesitan un enfoque diferente. Encuentra dónde se anula el numerador y denominador, haz una tabla de signos, y marca los intervalos donde la expresión es positiva o negativa.

Con sistemas de inecuaciones, resuelve cada una por separado y luego busca la intersección de las soluciones. Es como encontrar el horario que le va bien a todo tu grupo de amigos.

💡 Método: En inecuaciones fraccionarias, nunca multipliques por la variable sin saber su signo. Mejor haz tabla de signos.

Inecuaciones con Dos Incógnitas

Las inecuaciones con dos incógnitas se resuelven gráficamente, y es bastante visual una vez que le pillas el truco. Primero conviertes la inecuación en ecuación $cambias ≥ por =$.

Despejas la y, haces una tabla de valores y dibujas la recta. Luego usas el punto (0,0) para saber de qué lado de la recta tienes que colorear la solución.

En sistemas de inecuaciones, dibujas todas las rectas y buscas la zona donde se cumplen todas las condiciones a la vez. Es como encontrar el área común de varios círculos superpuestos.

💡 Visual: Usa diferentes colores para cada inecuación. La solución está donde se solapan todos los colores.

Repaso: Sistemas y Logaritmos

Este repaso mezcla sistemas con logaritmos y sistemas de dos incógnitas típicos de examen. En logaritmos, recuerda que log(a) + log(b) = log(a·b) y que log$10^n$ = n.

Para resolver sistemas mixtos, a veces tienes que ser creativo. Puedes usar sustitución $como x + y = 11$ o aprovechar identidades notables $como x² - y² = (x+y)(x-y)$.

Los sistemas gráficos son más fáciles de lo que parecen. Cada ecuación es una línea, y la solución está donde se cruzan. Haz tabla de valores para cada ecuación y dibuja.

💡 Exam tip: En logaritmos, siempre verifica que tus soluciones no anulen los argumentos. ¡No puede haber log de números negativos!

Funciones: Dominios y Definiciones

El dominio de una función son todos los valores de x que puedes meter sin que explote matemáticamente. Es súper importante para no cometer errores en los exámenes.

Para funciones racionales (con fracciones), el denominador no puede ser cero. Para raíces de índice par, lo de dentro debe ser positivo. Para logaritmos, el argumento debe ser positivo.

Las funciones se pueden expresar de varias formas: mediante ecuaciones, tablas de valores o gráficas. Todas dicen lo mismo, solo cambia el "idioma" matemático.

💡 Método sistemático: 1) Iguala denominadores a 0, 2) En raíces pares, lo de dentro ≥ 0, 3) En logaritmos, argumento > 0.

Funciones Compuestas e Inversas

Las funciones compuestas son como matrioskas: una función dentro de otra. (g∘f)(x) = g(f(x)) significa que primero aplicas f, luego g al resultado.

Para las funciones inversas, es un baile de variables: cambias f(x) por y, intercambias x e y, despejas la nueva y, y esa es tu función inversa. Es como deshacer los pasos de la función original.

El truco está en ser ordenado con los pasos. Si f convierte 2 en 5, entonces f⁻¹ debe convertir 5 en 2. Es la función que "deshace" lo que hizo la original.

💡 Comprobación: f(f⁻¹(x)) = x siempre. Si no te sale, revisa los cálculos.

Propiedades de Funciones y Modelos

Las propiedades globales de las funciones son como su DNI: te dicen todo sobre su comportamiento. Simetría, periodicidad, puntos de corte, continuidad... cada una cuenta una historia.

Las funciones logarítmicas tienen forma característica: crecen muy rápido al principio y luego se van aplanando. Su dominio son los números positivos.

Las funciones a trozos son como cambios de marcha en un coche: diferentes reglas para diferentes intervalos de x. Estudia cada trozo por separado, luego junta todo.

💡 Análisis completo: Dominio, recorrido, crecimiento, decrecimiento, puntos de corte. En ese orden y no te saltarás nada importante.