Funciones Polinómicas

Las funciones polinómicas son tus mejores amigas porque son predecibles y siempre continuas. Con f(x) = x³ - 6x², tienes todo lo que necesitas para un análisis completo.

El dominio siempre es todos los reales (ℝ), así que ya tienes un punto ganado. Para los puntos de corte, iguala a cero: x²$x-6$ = 0, que te da (0,0) y (6,0).

Para encontrar máximos y mínimos, deriva: f'(x) = 3x² - 12x = 0. Esto te da x = 0 y x = 4. Sustituye en la función original para las coordenadas y: (0,0) y (4,-32). La segunda derivada f''(x) = 6x - 12 te dice si es máximo (f'' < 0) o mínimo (f'' > 0).

¡Truco clave! El punto de inflexión siempre está entre el máximo y el mínimo. En este caso: f''(x) = 0 nos da x = 2, punto (2,-16).

Funciones Logarítmicas

Las funciones logarítmicas como f(x) = log₅$x² - 1$ tienen sus propias reglas especiales. Lo primero: el argumento del logaritmo debe ser positivo, así que x² - 1 > 0, lo que te da Dom = ℝ - {-1, 1}.

Los puntos de corte con el eje y se calculan con x = 0, pero aquí no existe porque -1 no está en el dominio. Para el eje x, igualas la función a cero: x² - 1 = 1, que te da x = ±√2.

Las asíntotas verticales aparecen donde el argumento se hace cero: x = ±1. Para los puntos clave, igualas el argumento a la base: x² - 1 = 5, dando x = ±√6 con coordenadas y = 1 siempre.

Recuerda: Las funciones logarítmicas tienen simetría par cuando f$-x$ = f(x), como en este caso.

Funciones Racionales

Las funciones racionales como f(x) = x/$x+1$² son las más completas porque tienen de todo: asíntotas, máximos, mínimos y puntos de inflexión.

El dominio excluye valores que hacen cero el denominador: ℝ - {-1}. El único punto de corte es (0,0) porque tanto el numerador como la función se anulan cuando x = 0.

Para las asíntotas, tienes una vertical en x = -1 $límites laterales dan -∞$ y una horizontal en y = 0 (grado del numerador < grado del denominador). La derivada f'(x) = $-x+1$/$x+1$³ = 0 te da el máximo en x = 1, punto (1, 1/4).

Dato importante: El recorrido está limitado por el valor del máximo: (-∞, 1/4).

Funciones Exponenciales

Las funciones exponenciales como f(x) = 3ˣ son las más sencillas de analizar. Siempre tienen dominio ℝ y son continuas en todo su dominio.

El único punto de corte es con el eje y en (0,1), porque 3⁰ = 1. No hay puntos de corte con el eje x porque 3ˣ nunca vale cero.

La asíntota horizontal está en y = 0 cuando x → -∞. La función es siempre creciente porque la derivada f'(x) = 2ln3 · 3ˣ > 0 para todo x. También tiene concavidad positiva en todo su dominio.

Regla práctica: Si el exponente es positivo, la función crece; si es negativo, decrece.

Para las asíntotas oblicuas, divide los polinomios: si tienes x²+4/x = x + 4/x, la asíntota oblicua es y = x.

Funciones Trigonométricas - Seno

Las funciones trigonométricas como f(x) = sen(2x) tienen patrones que se repiten cada cierto intervalo. El dominio siempre es ℝ y son continuas.

Los puntos de corte con el eje x salen de 2x = 0°, 180°, 360°..., dando x = 0° + 90°k. Para encontrar máximos y mínimos, deriva: f'(x) = 2cos(2x) = 0, lo que da cos(2x) = 0.

La segunda derivada f''(x) = -4sen(2x) te dice si es máximo (negativo) o mínimo (positivo). Los máximos están en x = 45° + 180°k y los mínimos en x = 135° + 180°k.

Regla de oro: Los senos son siempre funciones impares, los cosenos son pares.

El período es 180° (el número que acompaña a k en máximos y mínimos). El recorrido es [-1, 1] porque los valores del seno oscilan entre -1 y 1.

Funciones Trigonométricas - Tangente

La tangente f(x) = tan$x/2$ es especial porque tiene asíntotas verticales y es discontinua. Su dominio excluye los puntos donde cos$x/2$ = 0.

Para el dominio, buscas donde x/2 = 90°, 270°, 450°..., que da x = 180° + 360°k. Los puntos de corte salen de tan$x/2$ = 0, dando x = 0° + 360°k.

Las asíntotas verticales están en x = 180° + 360°k, con límites laterales que van a ±∞. La derivada f'(x) = 1/2$1 + tan²(x/2)$ > 0 siempre, así que es creciente en todo su dominio.

Característica única: Las tangentes y cotangentes son siempre impares y discontinuas.

El período es 360° y el recorrido es ℝ. Para la concavidad, los puntos de inflexión están en x = 0° + 360°k, alternando entre positiva y negativa.

Funciones Trigonométricas - Secante

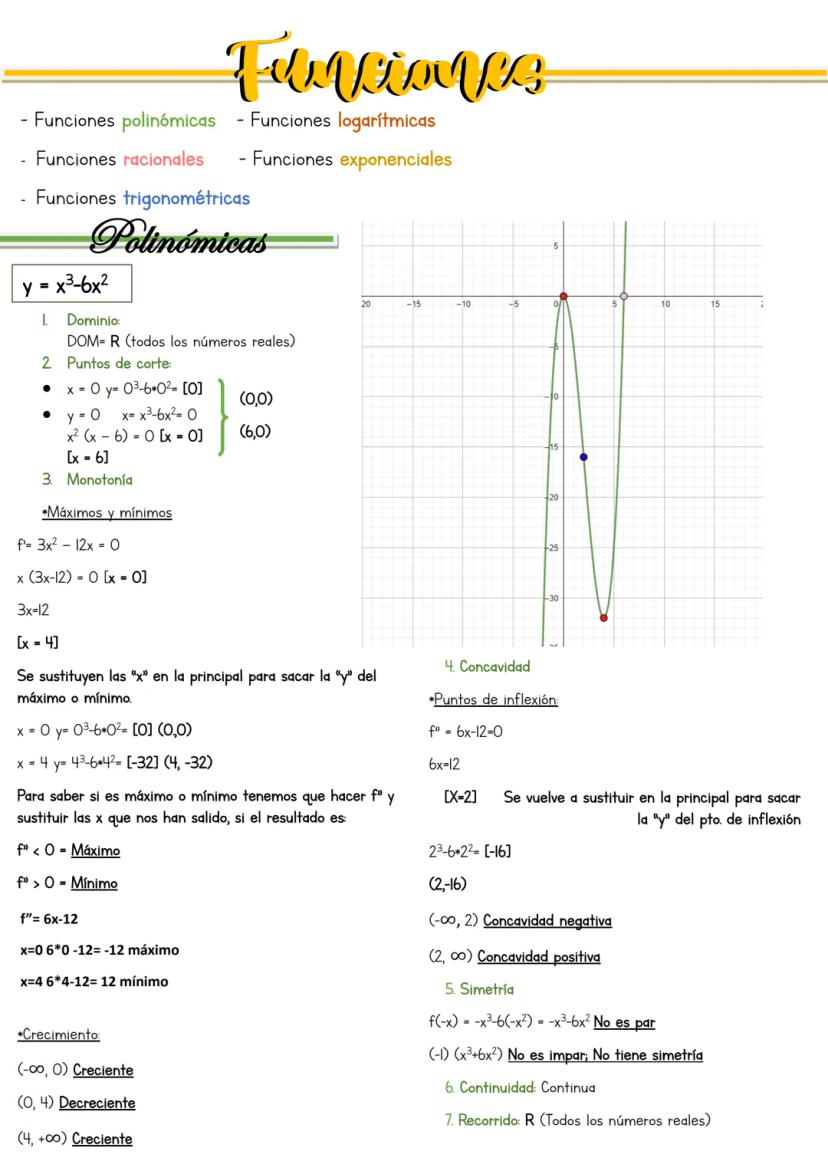
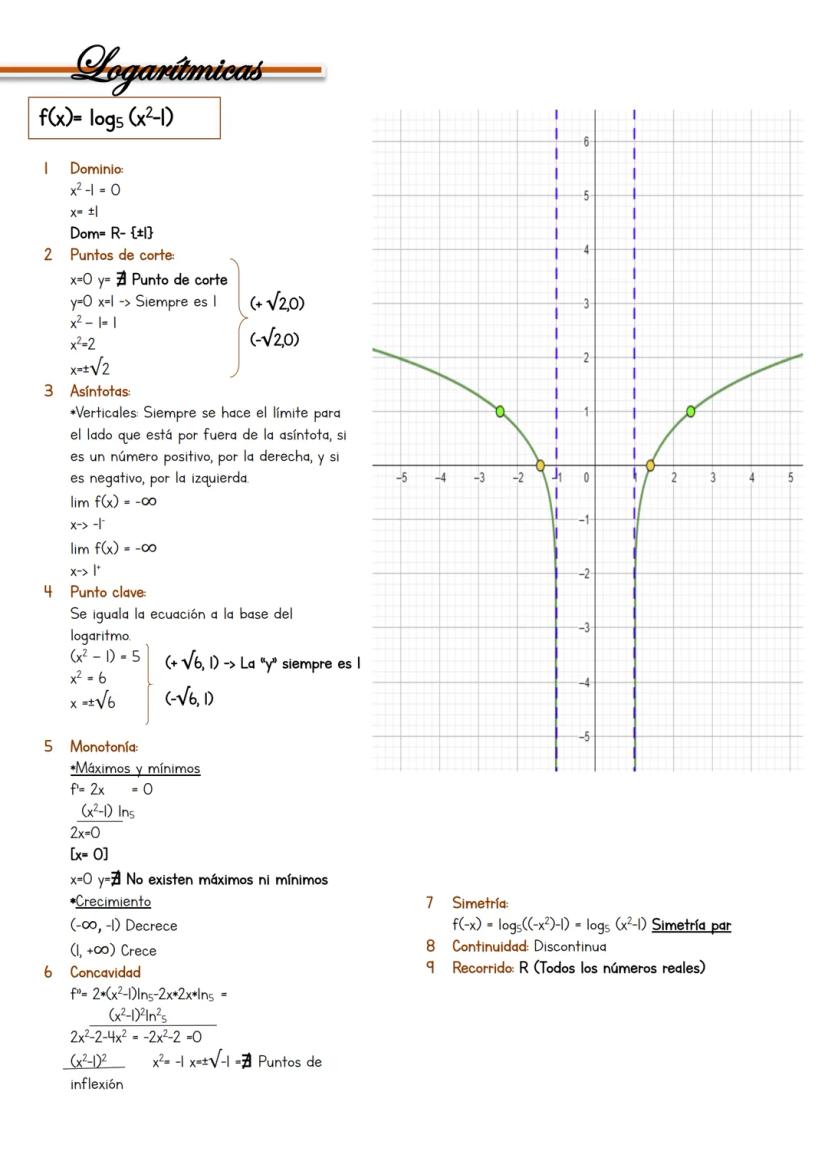
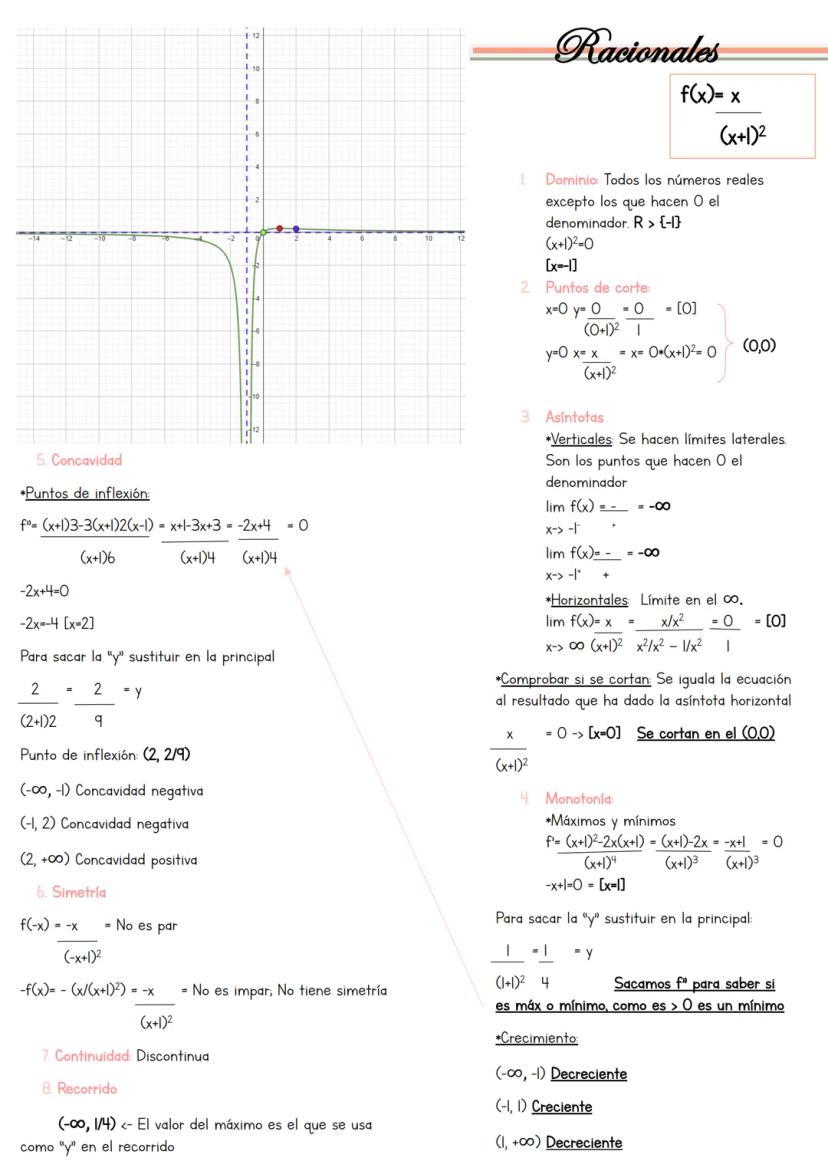
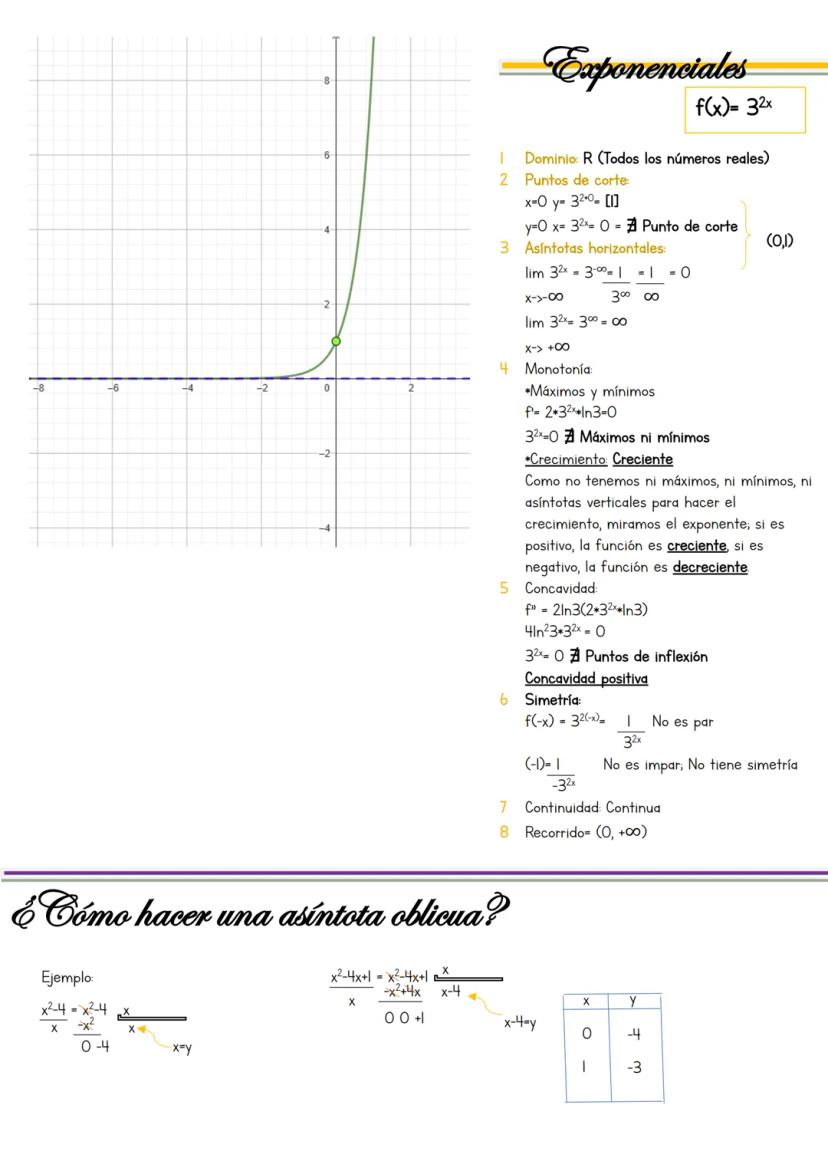
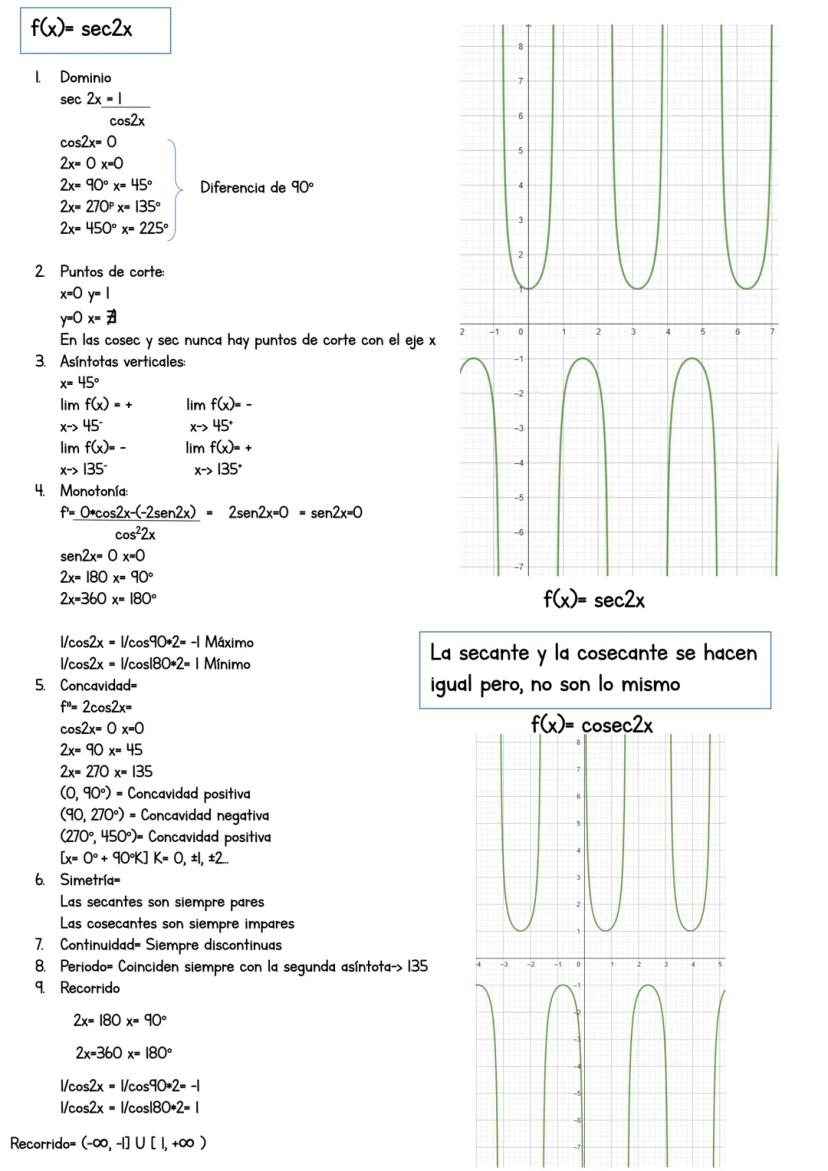
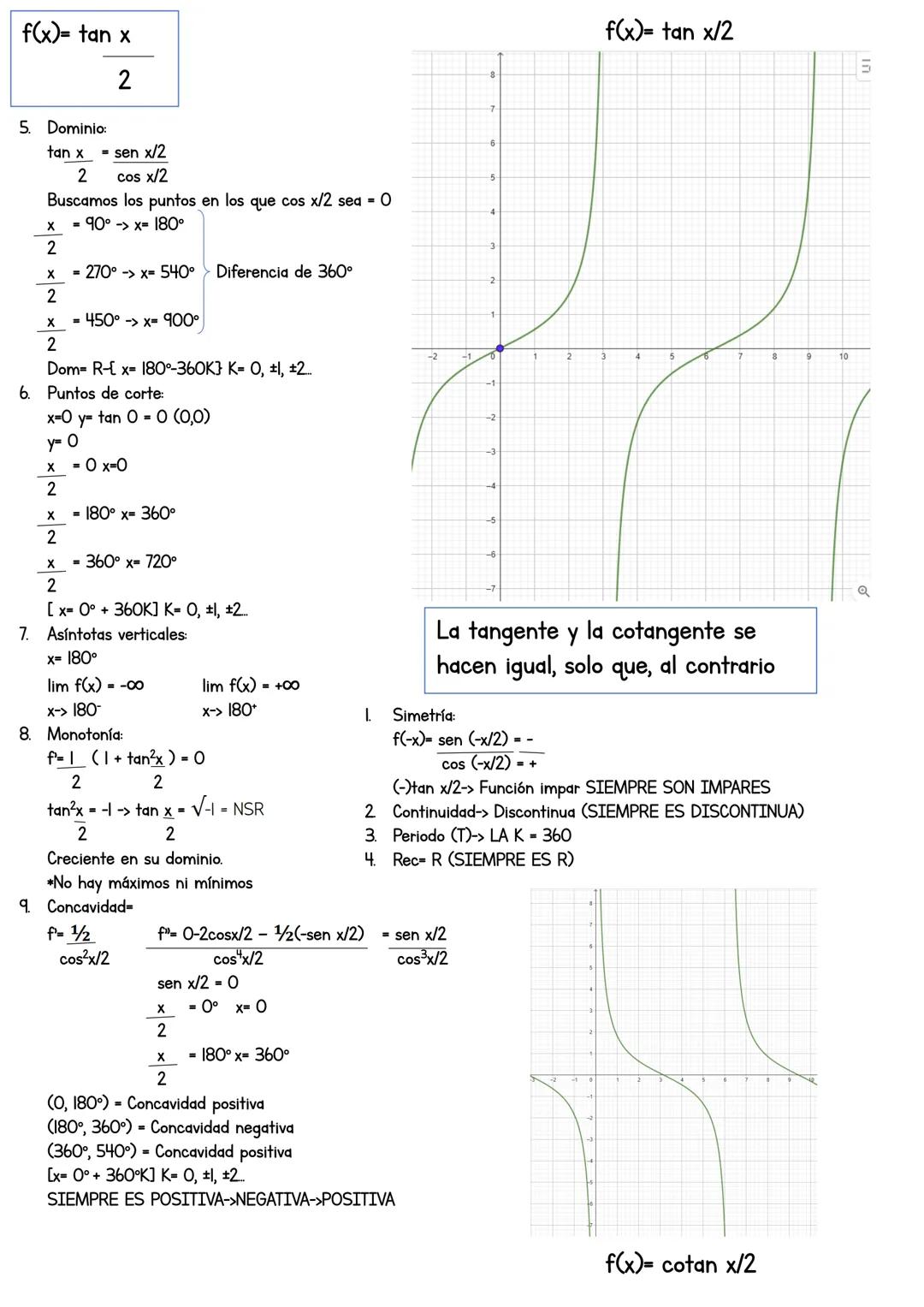
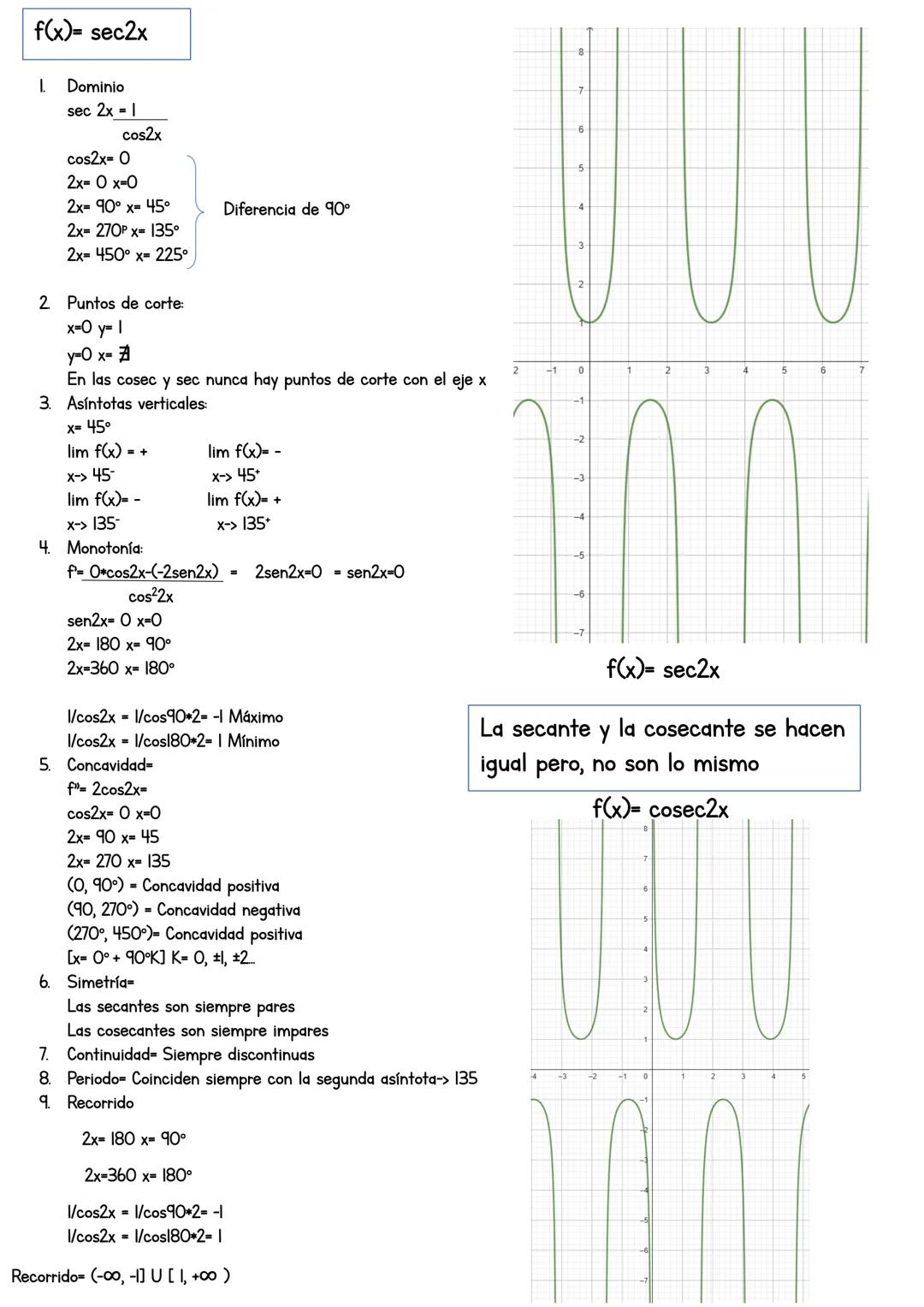
La secante f(x) = sec(2x) = 1/cos(2x) es la inversa del coseno, lo que la hace especial. Su comportamiento depende completamente de donde el coseno se anula.

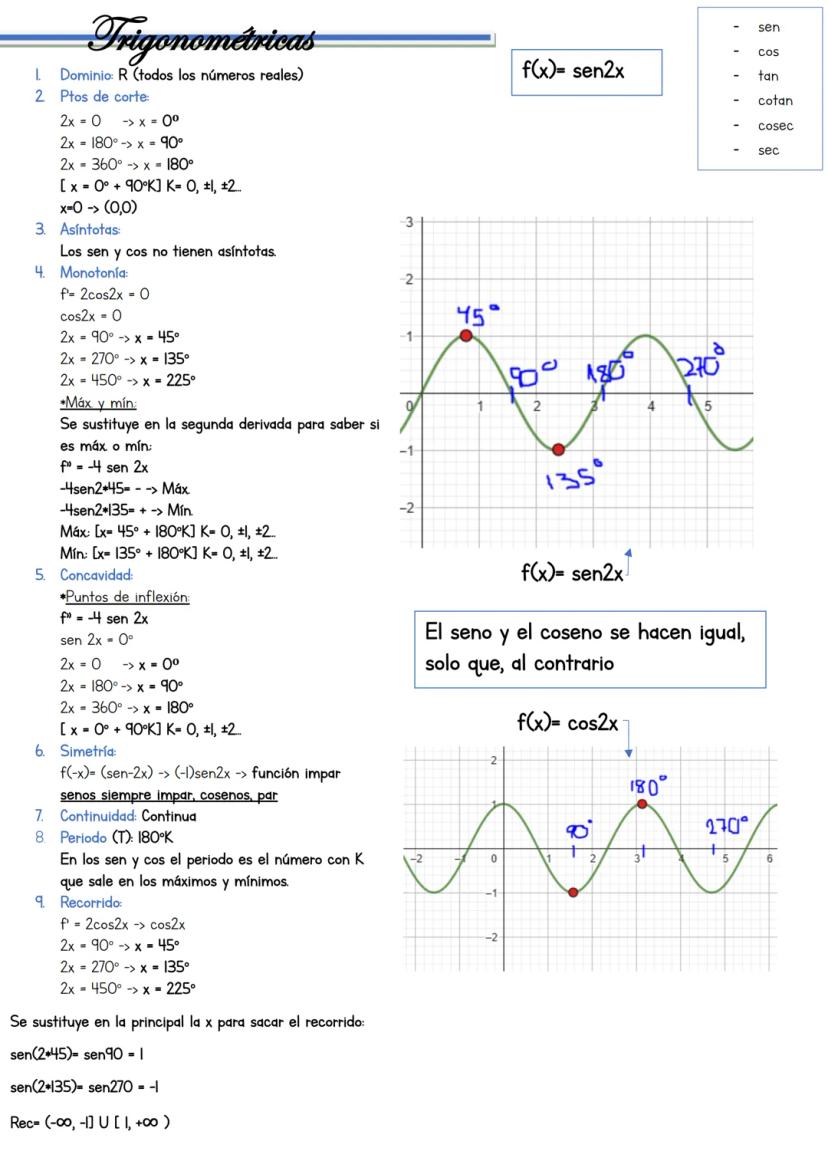
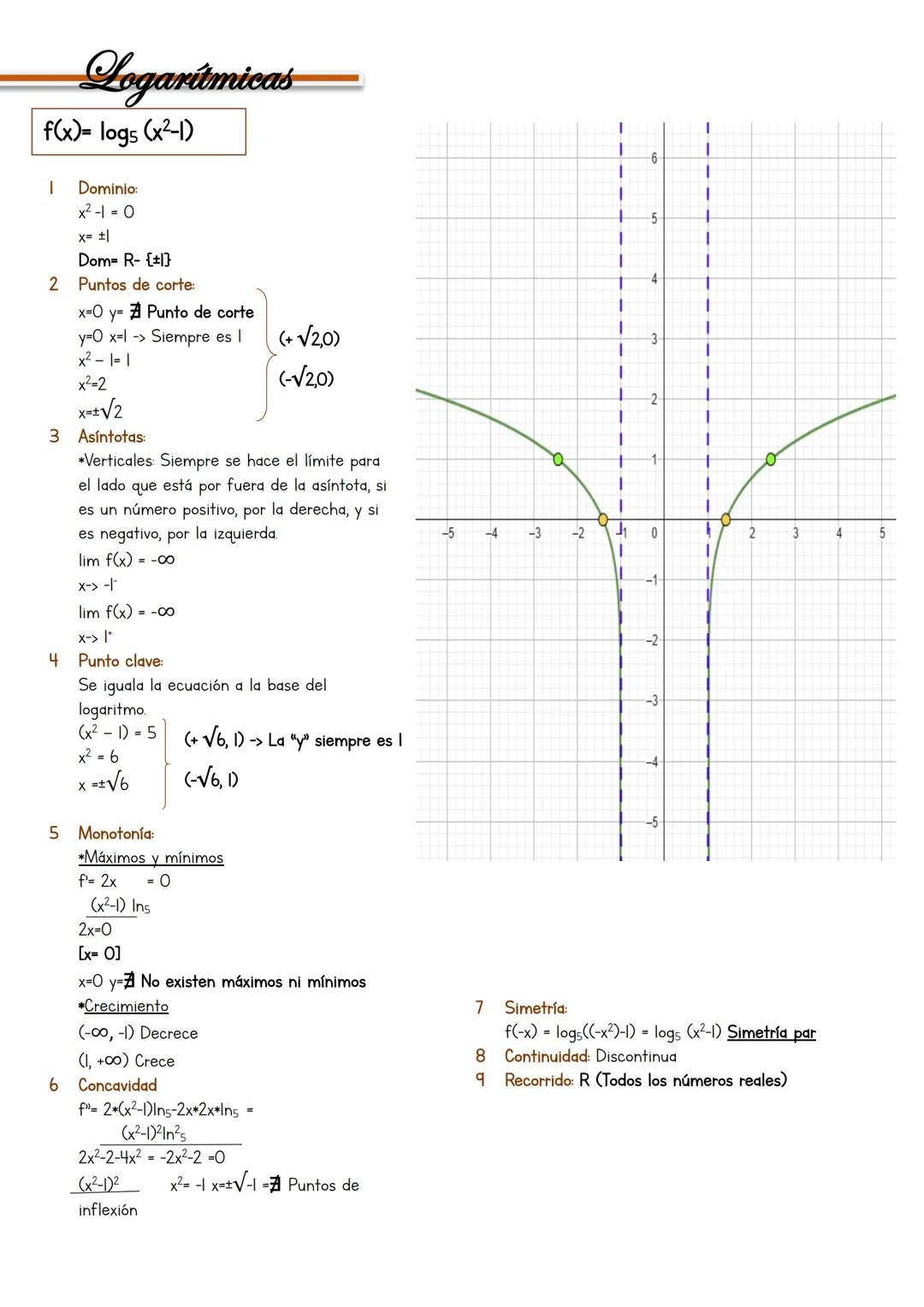
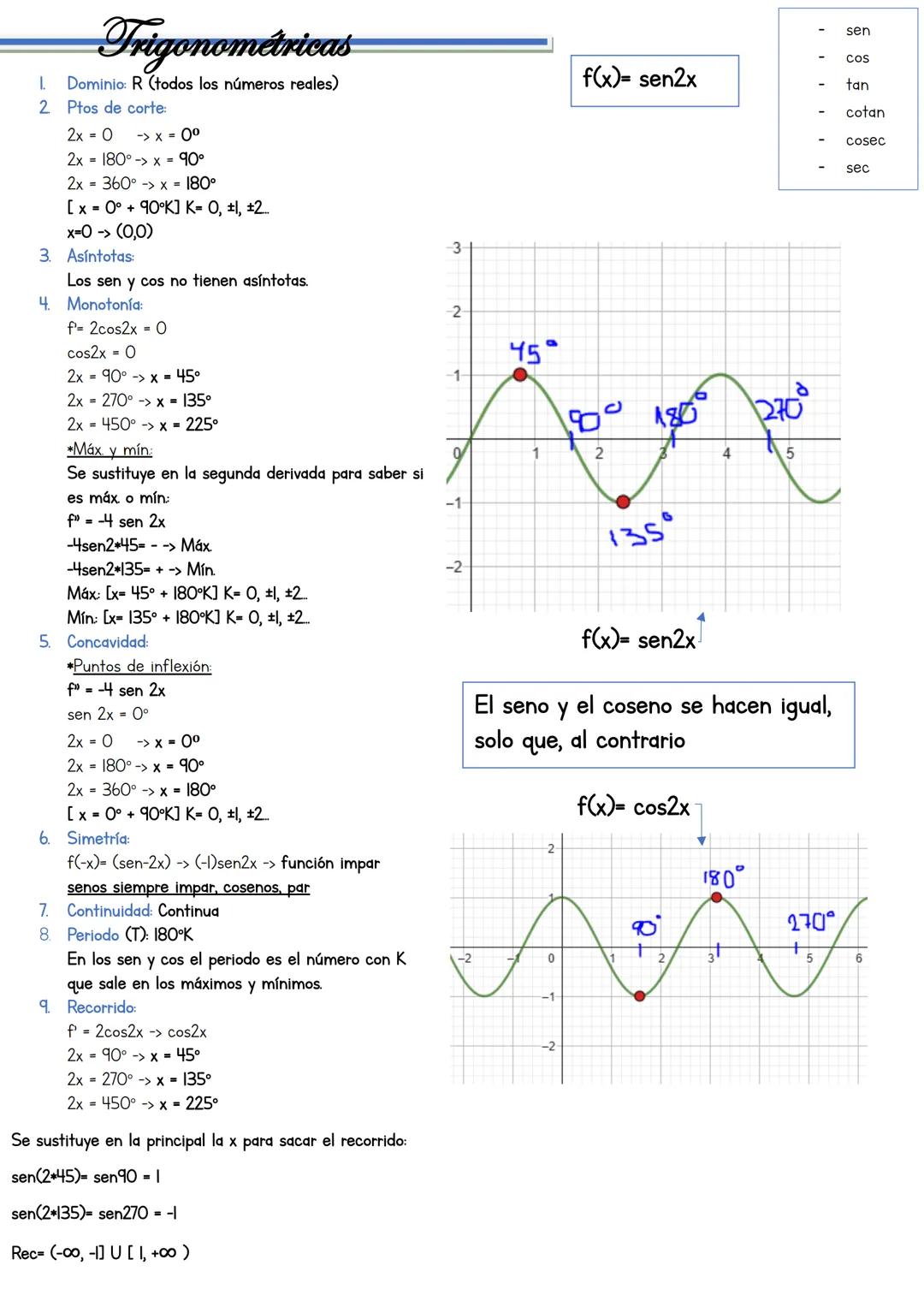
El dominio excluye donde cos(2x) = 0: x ≠ 45°, 135°, 225°... El único punto de corte es (0,1) porque sec(0) = 1. Las secantes y cosecantes nunca cortan el eje x.

Las asíntotas verticales están en x = 45°, 135°... con límites que alternan entre +∞ y -∞. Para máximos y mínimos, deriva: f'(x) = -2sen(2x)/cos²(2x) = 0, que da x = 90°, 180°...

Regla especial: En secantes y cosecantes, el recorrido es (-∞, -1] ∪ [1, +∞).

La función tiene período de 180° y es siempre discontinua. Los valores oscilan entre máximos y mínimos de ±1, pero nunca pasan por el intervalo (-1, 1).