Poliedros: Las figuras con muchas caras

Los poliedros son como los edificios del mundo matemático: tienen caras planas que se conectan entre sí. Imagínate un dado: eso es un poliedro perfecto.

Todo poliedro tiene tres elementos básicos que debes conocer. Las caras son los polígonos que forman las paredes, las aristas son las líneas donde se juntan dos caras, y los vértices son los puntos donde se encuentran tres o más aristas.

Hay dos tipos principales: convexos (como una pelota de fútbol) y cóncavos (con partes que se "hunden" hacia adentro). Los convexos son más fáciles de trabajar porque cumplen una regla genial llamada fórmula de Euler: C + V = A + 2.

¡Truco para recordar! En la fórmula de Euler, siempre suma las caras y vértices, luego comprueba si es igual a las aristas más 2.

Poliedros regulares y cuerpos de revolución

Solo existen cinco poliedros regulares en todo el universo matemático. Son como los "elegidos" porque todas sus caras son polígonos regulares idénticos: tetraedro (4 caras), cubo (6 caras), octaedro (8 caras), dodecaedro (12 caras) e icosaedro (20 caras).

El cubo es el más fácil de visualizar porque lo ves constantemente. Tiene seis caras cuadradas perfectas y en cada vértice se juntan exactamente tres aristas.

Los cuerpos de revolución son totalmente diferentes. Se forman cuando haces girar una figura plana alrededor de un eje, como cuando giras una moneda y parece una esfera. La línea exterior que gira se llama generatriz, y el eje alrededor del cual gira es el eje de rotación.

¡Dato curioso! Los antiguos griegos ya conocían estos cinco poliedros regulares hace más de 2000 años.

Prismas: Como edificios con plantas idénticas

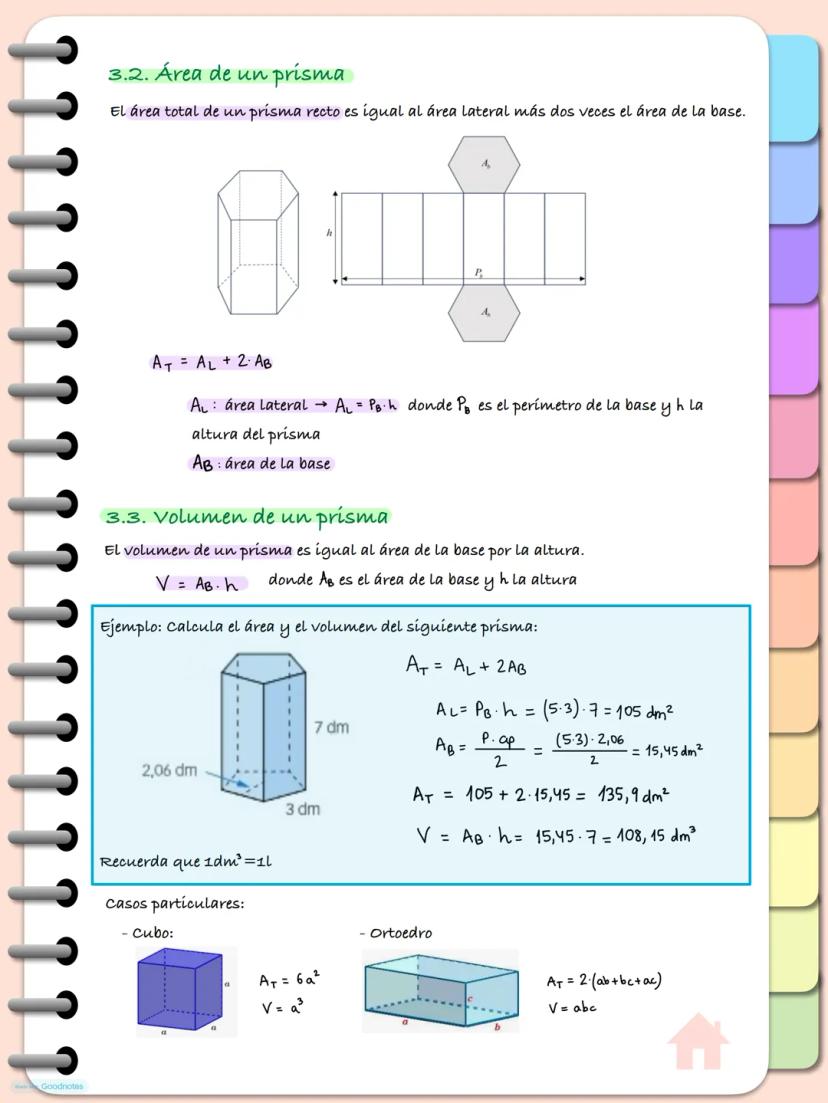
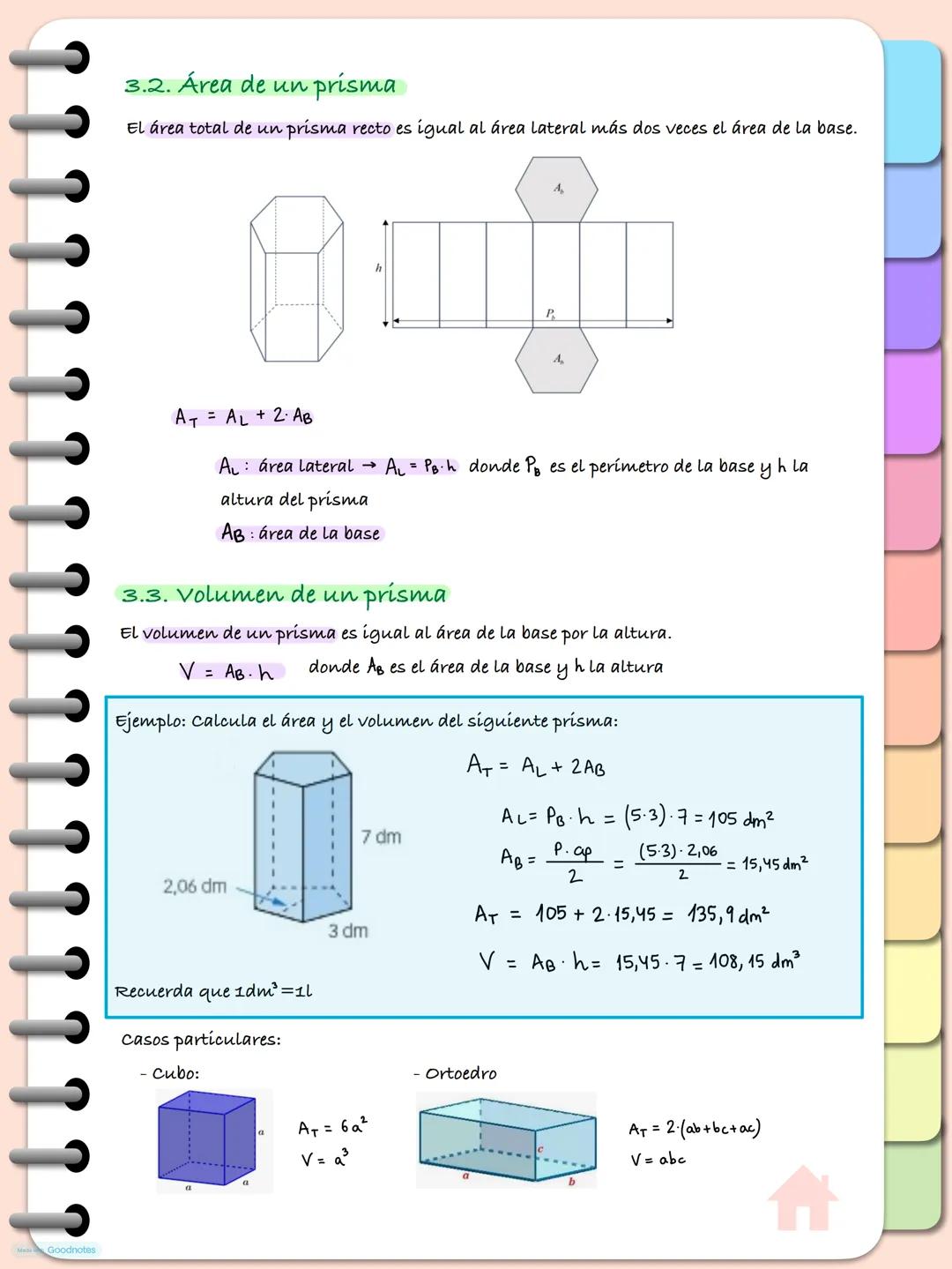
Un prisma es como un edificio donde todas las plantas tienen exactamente la misma forma. Tiene dos bases iguales y paralelas, conectadas por caras laterales que son paralelogramos.

Los prismas se nombran según la forma de su base: triangular, cuadrangular, pentagonal, etc. Los casos más famosos son el cubo (base cuadrada) y el ortoedro (base rectangular, como una caja de zapatos).

Si las aristas laterales son perpendiculares a la base, el prisma es recto. Si además la base es un polígono regular, entonces es un prisma regular. Para dibujar su desarrollo plano, simplemente "desenvuelves" todas las caras sobre el papel.

El desarrollo siempre incluye las dos bases y tantos rectángulos como lados tenga la base. Es como desarmar una caja de cartón para ver cómo estaba hecha.

¡Consejo práctico! Para visualizar un desarrollo plano, imagina que cortas las aristas de una caja de cereal y la abres completamente.

Área y volumen de prismas

Calcular el área total de un prisma es súper sencillo: sumas el área lateral más dos veces el área de la base. La fórmula es AT = AL + 2AB.

Para el área lateral, multiplicas el perímetro de la base por la altura $AL = PB × h$. Es como si envolvieras el prisma con papel de regalo alrededor de sus lados.

El volumen es aún más fácil: área de la base por altura $V = AB × h$. Piénsalo como apilar copias de la base una encima de otra hasta llegar a la altura total.

Los casos especiales son geniales de recordar. Para un cubo: área = 6a² y volumen = a³. Para un ortoedro: área = 2$ab + bc + ac$ y volumen = abc.

¡Recuerda! El volumen siempre se mide en unidades cúbicas (cm³, m³), y 1 dm³ = 1 litro.

Pirámides: Puntiagudas como las de Egipto

Las pirámides son poliedros con una base poligonal y caras laterales triangulares que se juntan en un punto llamado vértice. Son como las pirámides de Egipto, pero pueden tener cualquier polígono como base.

La altura es la distancia vertical desde la base hasta el vértice. La apotema es la altura de cada cara lateral triangular, y es clave para calcular áreas.

Las pirámides se clasifican igual que los prismas: son rectas cuando las caras laterales son triángulos isósceles, y regulares cuando además la base es un polígono regular.

Para el desarrollo plano, dibujas la base y le pegas tantos triángulos como lados tenga la base. Si la pirámide es regular, todos los triángulos son idénticos.

¡Dato increíble! Las pirámides de Egipto son prácticamente pirámides regulares cuadrangulares perfectas.

Área y volumen de pirámides

El área total de una pirámide suma el área lateral más el área de la base: AT = AL + AB. El área lateral se calcula con la fórmula AL = (PB × ap)/2, donde PB es el perímetro de la base y ap es la apotema.

El volumen de una pirámide siempre es un tercio del volumen de un prisma con la misma base y altura: V = (1/3) × AB × h. Es como si una pirámide fuera exactamente la tercera parte de un prisma.

Para encontrar la apotema, normalmente usas el teorema de Pitágoras. La apotema, la altura y la apotema de la base forman un triángulo rectángulo perfecto.

Los cálculos pueden parecer complicados al principio, pero siguiendo los pasos ordenadamente siempre llegas al resultado correcto. Primero encuentra todas las medidas que necesitas, luego aplica las fórmulas.

¡Truco de memoria! El volumen de la pirámide es siempre 1/3 del prisma equivalente.

Más ejemplos de pirámides

Cuando trabajas con pirámides hexagonales, recuerda que en un hexágono regular el radio es igual al lado. Esto te ayuda muchísimo para encontrar la altura usando Pitágoras.

Para calcular la apotema de la base en polígonos regulares, siempre puedes usar la relación entre el lado, el radio y la apotema. En hexágonos, triangulos equiláteros y pentágonos regulares hay fórmulas específicas.

Los problemas más complejos requieren varios pasos, pero la lógica es siempre la misma. Primero encuentras la apotema de la pirámide, luego la apotema de la base, y finalmente aplicas las fórmulas de área y volumen.

No te agobies si los números salen con decimales. Es completamente normal en geometría espacial, y tu calculadora es tu mejor amiga para las raíces cuadradas.

¡Consejo de estudio! Practica dibujando los triángulos rectángulos que se forman para aplicar Pitágoras correctamente.

Cilindros: Perfectamente redondos

El cilindro es un cuerpo de revolución que obtienes al hacer girar un rectángulo alrededor de uno de sus lados. Piensa en una lata de refresco: esa es la forma perfecta de un cilindro.

Sus elementos son sencillos de entender. Las bases son dos círculos idénticos, el eje es la línea alrededor de la cual gira, y la generatriz es el lado del rectángulo que crea la superficie curva.

El desarrollo plano de un cilindro es genial: dos círculos (las bases) y un rectángulo cuyo ancho es la circunferencia de la base (2πr) y cuya altura es la altura del cilindro.

Para el área total usas: AT = AL + 2AB. El área lateral es AL = 2πrh (como si fuera la etiqueta que rodea una lata), y el área de cada base es AB = πr².

¡Visualízalo! Si quitas la etiqueta de una lata cilíndrica y la extiendes, obtienes exactamente el desarrollo plano.

Volumen del cilindro y conociendo el cono

El volumen del cilindro es súper directo: V = AB × h = πr²h. Es como si apilarias círculos desde la base hasta la altura total.

El cono es otro cuerpo de revolución fascinante. Se forma girando un triángulo rectángulo alrededor de uno de sus catetos. Imagínate un cucurucho de helado: esa es la forma perfecta.

Los elementos del cono son la base (un círculo), el eje (el cateto alrededor del cual gira), la generatriz (la hipotenusa del triángulo), y la altura (la distancia del vértice a la base).

El desarrollo plano del cono es más complejo: un círculo completo para la base y un sector circular para la superficie lateral. El sector parece un trozo de pizza gigante.

¡Dato interesante! La generatriz del cono siempre es mayor que su altura, porque es la hipotenusa del triángulo rectángulo que lo forma.

Área y volumen del cono

Para el área del cono sumas el área lateral más el área de la base: AT = AL + AB. El área lateral es AL = πrg (donde g es la generatriz) y el área de la base es AB = πr².

El volumen del cono sigue la misma regla que las pirámides: es un tercio del cilindro equivalente. La fórmula es V = (1/3) × AB × h = (1/3) × πr² × h.

Para encontrar la generatriz casi siempre necesitas Pitágoras: g² = h² + r². La generatriz, la altura y el radio forman un triángulo rectángulo perfecto.

Los problemas de conos son muy similares a los de pirámides en cuanto a metodología. Primero encuentras todas las medidas que necesitas, especialmente la generatriz, y luego aplicas las fórmulas paso a paso.

¡Recuerda la conexión! El cono es a la pirámide lo que el cilindro es al prisma: versiones "redondeadas" con fórmulas muy similares.