Conceptos Básicos de Vectores

Los vectores son como flechas que nos indican dirección y magnitud - piénsalos como instrucciones para llegar de un punto A a otro punto B. Para calcular un vector AB entre dos puntos A(a₁, a₂) y B(b₁, b₂), simplemente restas: AB = $b₁-a₁, b₂-a₂$.

El módulo de un vector es su "longitud" y se calcula con |u⃗| = √$u₁² + u₂²$. Es como medir cuántos pasos tienes que dar siguiendo esa flecha.

Para encontrar el argumento (el ángulo que forma con el eje X), usas la tangente: tg α = u₂/u₁. Por ejemplo, si tienes v⃗(4,3), entonces tg α = 3/4 = 0.75, y arc tg 0.75 ≈ 37°.

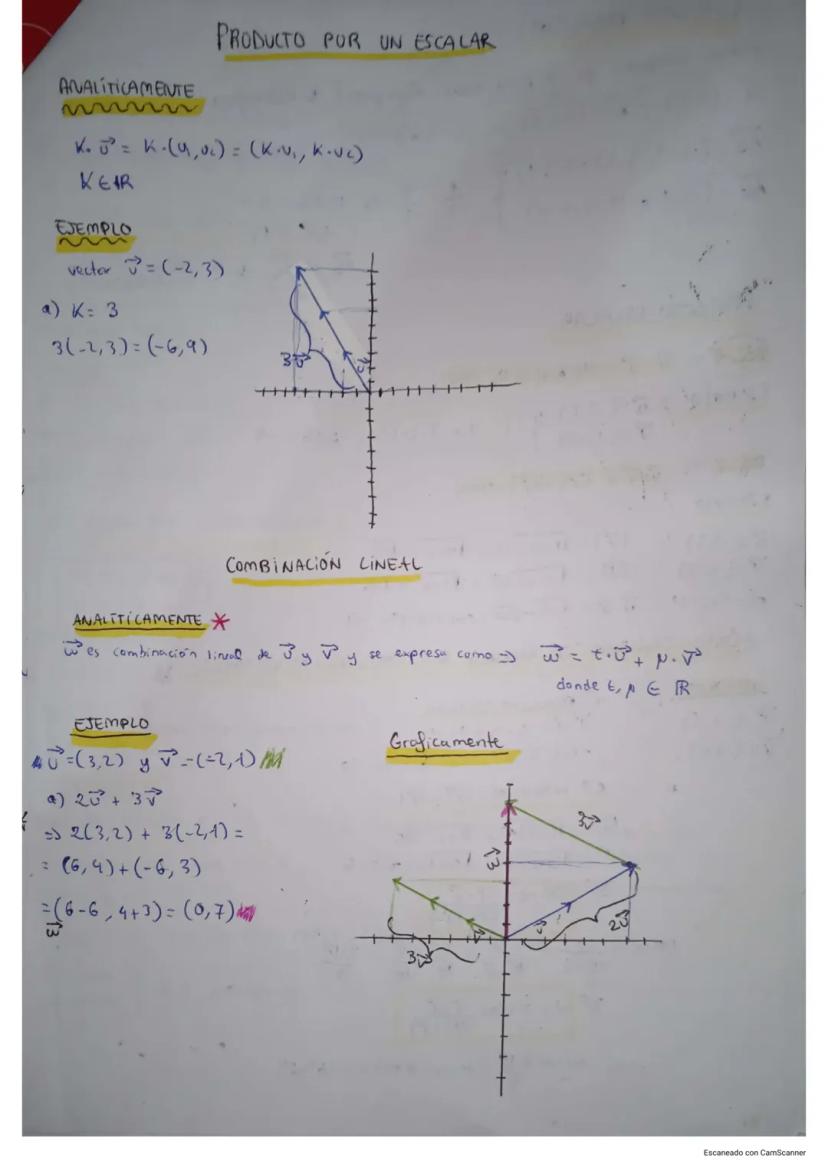
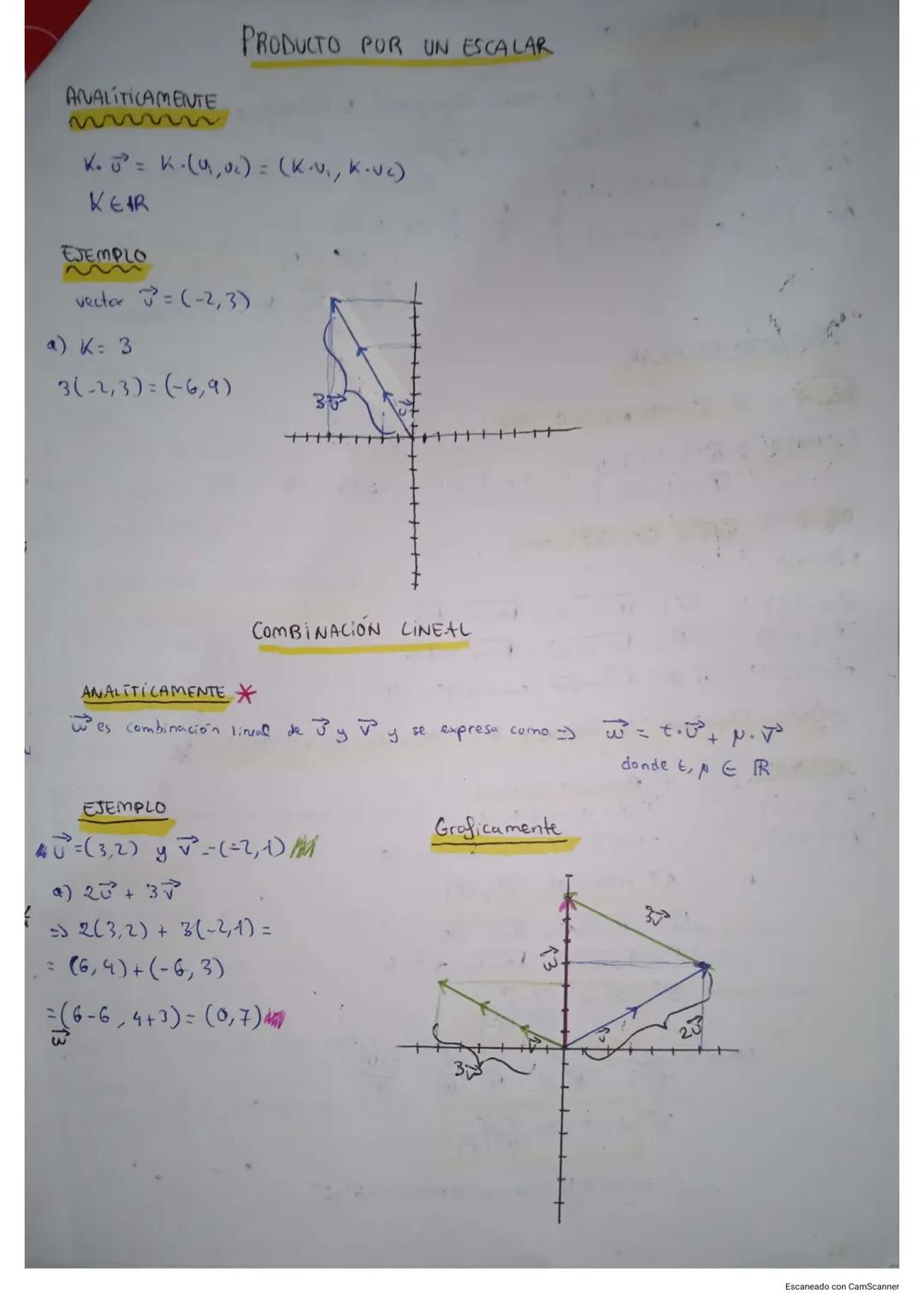
¡Truco! Para crear un vector paralelo, simplemente multiplica ambas componentes por el mismo número: si u⃗ = (-3, 3), entonces 2u⃗ = (-6, 6) es paralelo. Para uno perpendicular, intercambia las componentes y cambia el signo de una: si v⃗ = (3, 4), entonces n⃗ = (4, -3) es perpendicular.

Ecuaciones de la Recta: Paramétricas y Continuas

Las ecuaciones paramétricas te permiten describir cualquier punto de una recta usando un parámetro k. Si tienes r: x = -5-3k, y = 2-5k, puedes encontrar puntos dándole valores a k $k=0, k=1, k=-1...$.

La ecuación vectorial es la forma más elegante: (x,y) = (punto) + k(vector director). Para el ejemplo anterior sería (x,y) = (-5,2) + k(-3,-5).

La ecuación continua elimina el parámetro k y queda: $x-a$/u₁ = $y-b$/u₂. Es perfecta cuando necesitas trabajar sin parámetros.

¡Ojo! Para verificar si un punto pertenece a la recta, sustituye sus coordenadas. Si A(-3,2) está en nuestra recta, debe cumplir: -3 = -5-3k y 2 = 2-5k. Si obtienes valores diferentes de k, ¡el punto no pertenece!

Ecuación General y Posición de Rectas

La ecuación general (o implícita) tiene la forma ax + by + c = 0. Para obtenerla desde la continua, haces productos cruzados y ordenas términos. Por ejemplo, de $x+2$/5 = $y-5$/(-9) llegas a -9x - 5y + 7 = 0.

La posición relativa de dos rectas se determina comparando los coeficientes a/a', b/b' y c/c':

• Coincidentes: los tres cocientes son iguales
• Paralelas: a/a' = b/b' ≠ c/c'
• Secantes: a/a' ≠ b/b'

¡Súper útil! Para encontrar la ecuación general que pasa por dos puntos, primero calcula el vector director AB, luego usa un punto y la ecuación continua, y finalmente despeja para llegar a la forma ax + by + c = 0.

Paralelismo, Perpendicularidad y Ángulos

Para crear una recta paralela a r = 2x - 3y + 5 = 0 que pase por A(-2,4), mantén los coeficientes a y b iguales: s = 2x - 3y + c = 0. Sustituye el punto para hallar c.

Para una recta perpendicular, intercambia y cambia signo: si r tiene vector normal (2,-3), la perpendicular tendrá (3,2). Esto da s = 3x + 2y + c = 0.

El ángulo entre dos rectas se calcula con el producto escalar de sus vectores normales: cos α = (n⃗·n⃗')/(|n⃗||n⃗'|).

¡Recuerda! Dos rectas son perpendiculares cuando el producto escalar de sus vectores normales es cero. Y son paralelas cuando sus vectores normales son proporcionales.

Operaciones con Vectores

La suma de vectores es súper fácil: u⃗ + v⃗ = $u₁+v₁, u₂+v₂$. Gráficamente, colocas un vector tras el otro y el resultado va del origen al extremo final.

Para la resta, sumas el vector opuesto: u⃗ - v⃗ = u⃗ + $-v⃗$ = $u₁-v₁, u₂-v₂$. Por ejemplo, (-4,1) - (2,3) = (-6,-2).

El producto por un escalar k multiplica cada componente: k·u⃗ = (k·u₁, k·u₂). Si k > 1, el vector se alarga; si 0 < k < 1, se acorta; si k < 0, cambia de sentido.

¡Visualízalo! Imagínate los vectores como desplazamientos en un mapa. Sumar vectores es como seguir varias instrucciones consecutivas - el resultado final es tu posición total respecto al punto de partida.

Combinaciones Lineales y Productos Escalares

Una combinación lineal expresa un vector w⃗ como w⃗ = t·u⃗ + p·v⃗, donde t y p son números reales. Es como crear "recetas" mezclando vectores base.

Por ejemplo, con u⃗ = (3,2) y v⃗ = (-2,1), la combinación 2u⃗ + 3v⃗ = 2(3,2) + 3(-2,1) = (6,4) + (-6,3) = (0,7).

El producto escalar tiene dos definiciones equivalentes: u⃗·v⃗ = u₁v₁ + u₂v₂ o u⃗·v⃗ = |u⃗||v⃗|cos α. La primera es para calcular, la segunda para entender el significado geométrico.

¡Truco matemático! El producto escalar te dice si dos vectores van en la misma dirección (resultado positivo), opuesta (negativo) o son perpendiculares (resultado cero).

Vectores Paralelos y Cálculo de Ángulos

Para verificar si tres puntos están alineados, calcula dos vectores desde el primero y comprueba si son paralelos. Los vectores AB⃗ y AC⃗ son paralelos si u₁/v₁ = u₂/v₂.

El ángulo entre vectores se calcula en tres pasos: 1) Producto escalar, 2) Módulos de ambos vectores, 3) cos α = (u⃗·v⃗)/(|u⃗||v⃗|). Luego aplicas arcoseno para obtener el ángulo.

Por ejemplo, con u⃗ = (-2,1) y v⃗ = (-3,4): u⃗·v⃗ = 10, |u⃗| = √5, |v⃗| = 5, entonces cos α = 10/(√5·5) = 2√5/5, y α ≈ 26.56°.

¡Importante! Si el producto escalar es cero, los vectores son perpendiculares. Si es positivo, forman un ángulo agudo; si es negativo, obtuso.

Ecuaciones Vectorial y Paramétrica de la Recta

La ecuación vectorial es la más elegante: x⃗ = A⃗ + k·v⃗, donde A⃗ es un punto conocido y v⃗ el vector director. Para hallarla desde dos puntos, calcula primero el vector director AB⃗.

Las ecuaciones paramétricas separan las coordenadas: x = a + kv₁ e y = b + kv₂. Son perfectas para calcular puntos específicos dando valores a k.

Por ejemplo, si r = (5,3) + k(-1,4), las paramétricas serían x = 5-k e y = 3+4k. Para k=0 obtienes (5,3), para k=1 obtienes (4,7), etc.

¡Consejo práctico! Las ecuaciones paramétricas son ideales para programación y animación, mientras que la vectorial es perfecta para razonamiento matemático. ¡Domina ambas y serás imparable!