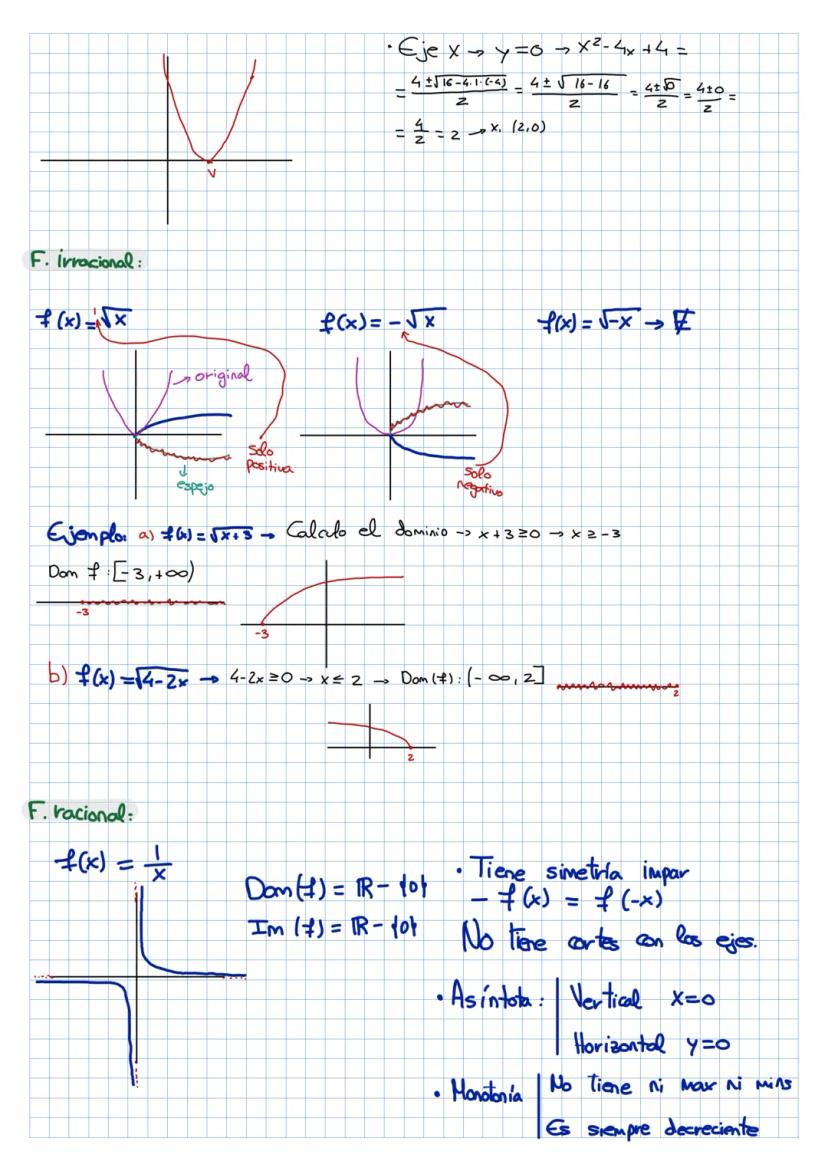
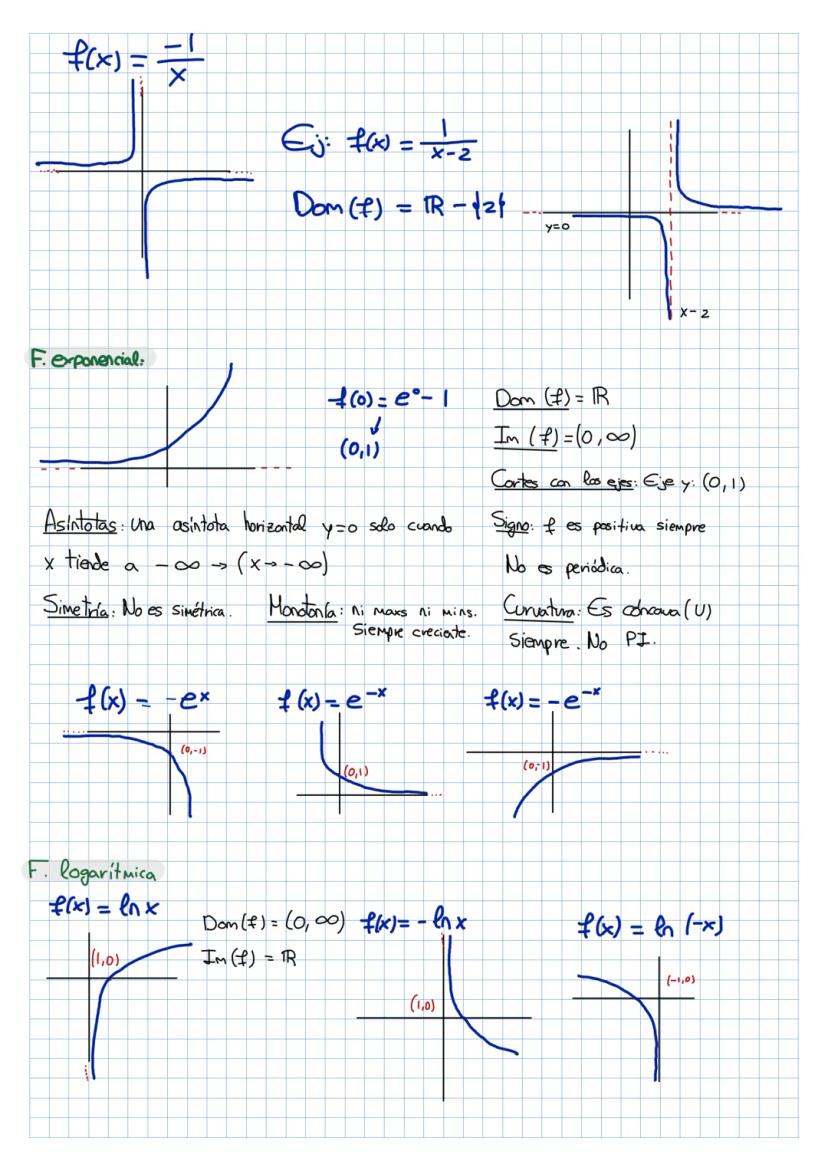
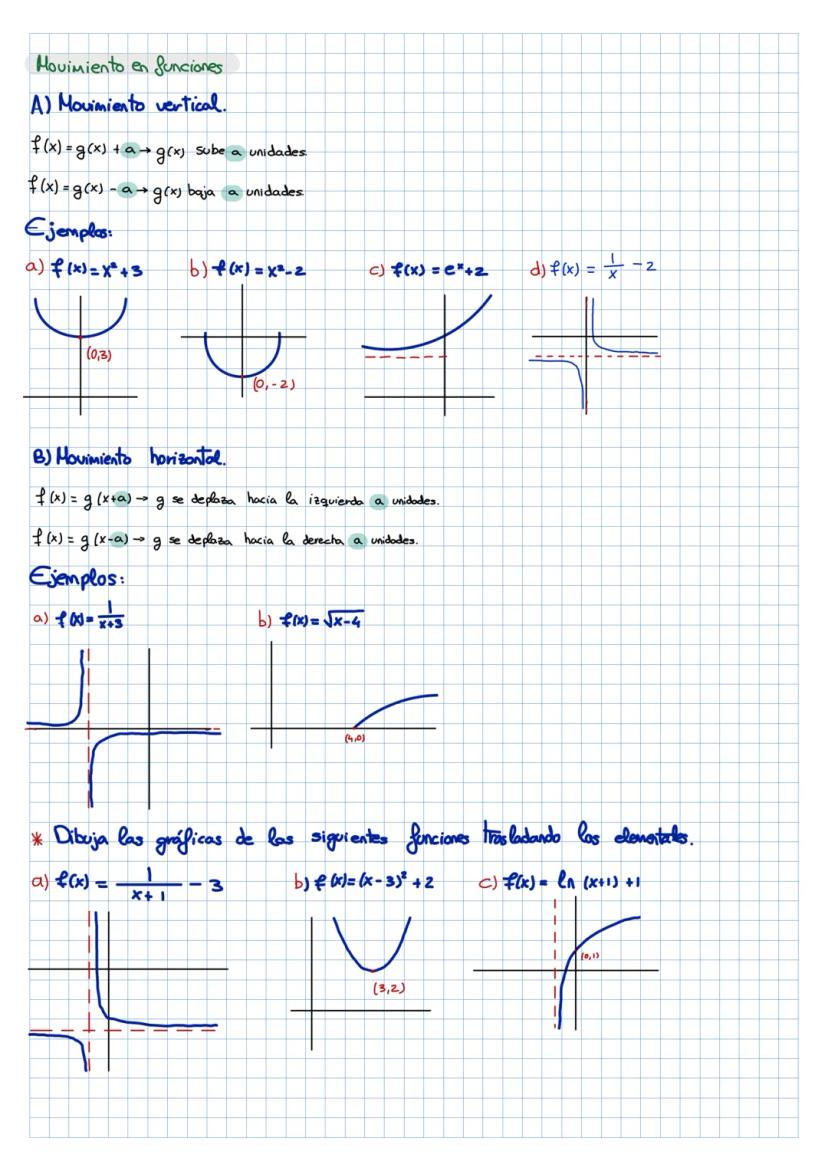
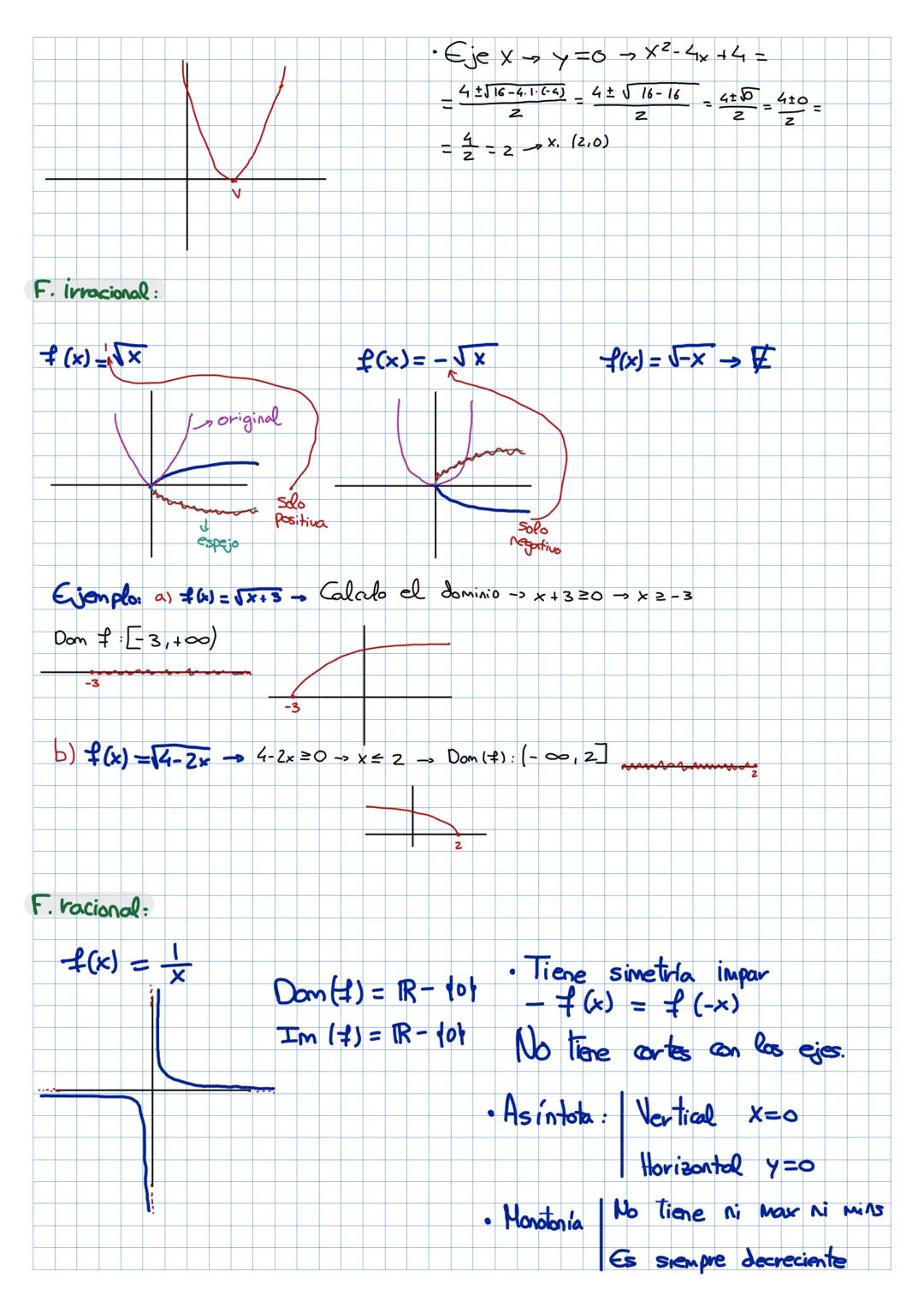
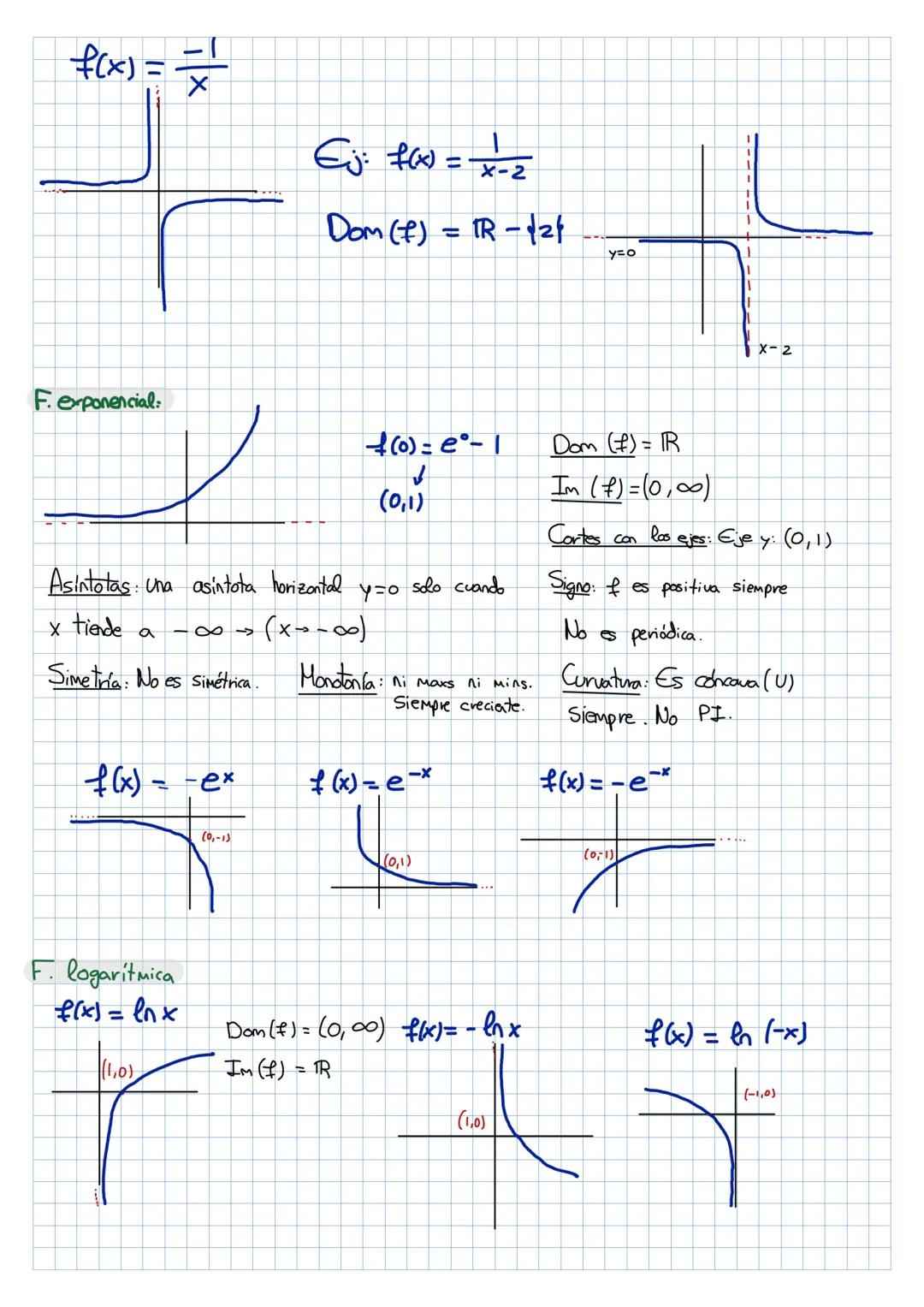
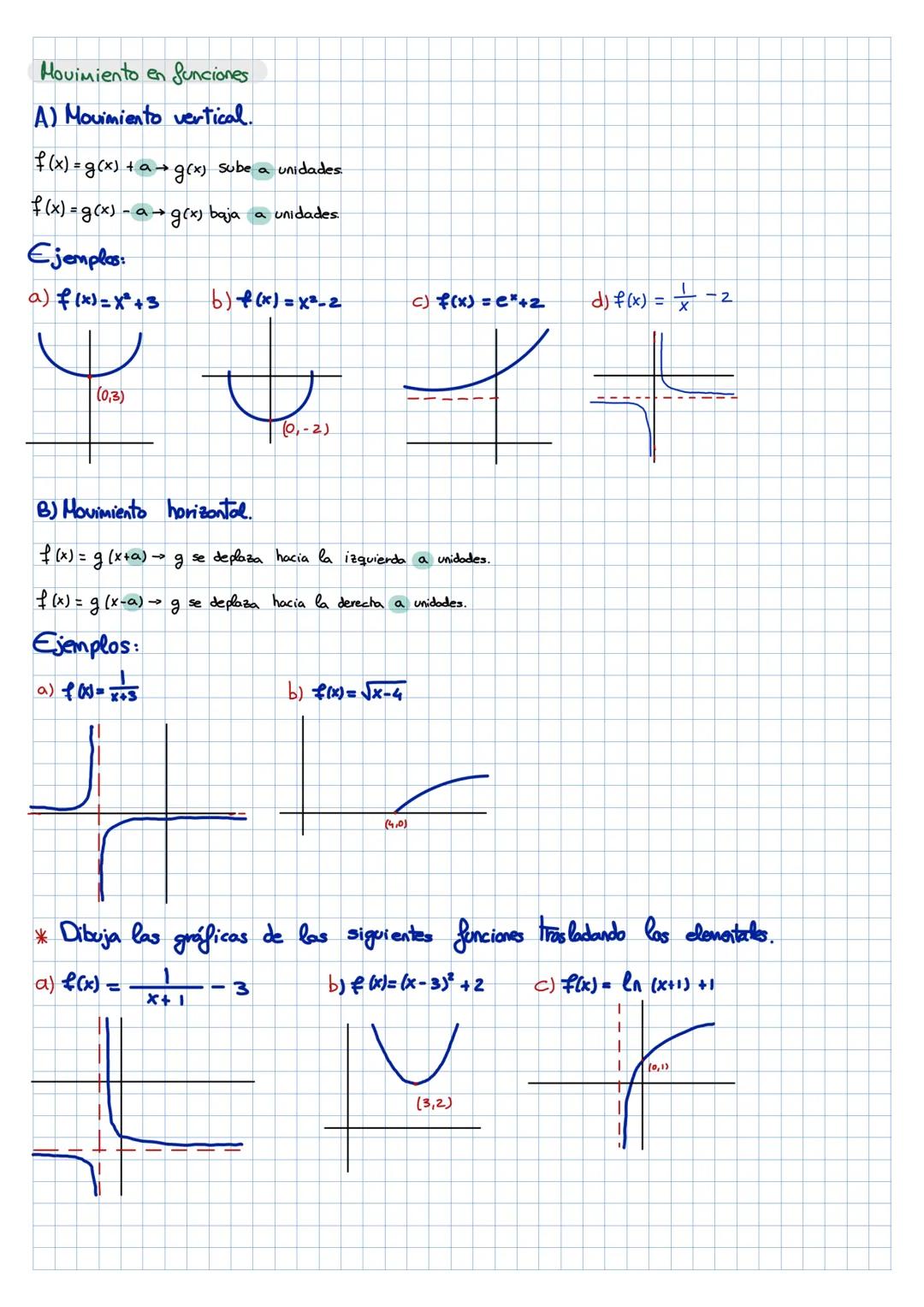
¡Las funciones y el análisis matemático pueden parecer complicados, pero... Mostrar más
Inscríbete para ver los apuntes¡Es gratis!
Acceso a todos los documentos
Mejora tus notas
Únete a millones de estudiantes
Al registrarte aceptas las Condiciones del servicio y la Política de privacidad.