Matemáticas

Continuidad y Discontinuidades de Funciones

discontinuidad removible

Matemáticas7885Actualizado 9 sept 20269 páginas

Conceptos Básicos: Funciones, Límites y Continuidad

Denunciar

Xiana@xiana_resumenes

Añadir a fuentes de Google

Las funciones son el corazón de las matemáticas de bachillerato, conectando dos magnitudes de forma que cada valor de x produce exactamente un valor de y. En este tema descubrirás cómo analizar funciones completamente: desde identificar su dominio hasta calcular límites complicados y determinar dónde son continuas.

Funciones, límites y continuidad – página 1

Inscríbete para ver los apuntes.
¡Es gratis!

Funciones y sus Características Básicas

¿Alguna vez te has preguntado por qué algunas gráficas representan funciones y otras no? La clave está en el test de la línea vertical: si puedes trazar cualquier línea vertical y esta corta la gráfica en más de un punto, entonces no es función.

Una función se escribe como y = f $x$ , donde x es la variable independiente e y la dependiente. Para dominar las funciones necesitas conocer sus características principales.

El dominio (Dom f $x$ ) son todos los valores que puede tomar x, mientras que el recorrido (Im f $x$ ) son todos los valores posibles de y. Los puntos de corte se encuentran haciendo y = 0 para el eje x, y x = 0 para el eje y.

La monotonía te dice si la función crece, decrece o se mantiene constante en diferentes intervalos. Los máximos y mínimos pueden ser absolutos (los más altos o bajos de toda la gráfica) o relativos (solo en una zona específica).

Truco clave: Para analizar la curvatura, imagina que conectas dos puntos con una línea recta. Si la curva queda por debajo, es cóncava hacia arriba; si queda por encima, es cóncava hacia abajo.

Funciones, límites y continuidad – página 2

Inscríbete para ver los apuntes.
¡Es gratis!

Funciones Polinómicas: Las Más Frecuentes en Selectividad

Las funciones lineales $y = mx$ son las más sencillas: siempre pasan por el origen, tienen dominio y recorrido infinitos, y poseen simetría impar. Las funciones constantes $y = k$ son líneas horizontales con simetría par.

Las funciones afín $y = mx + n$ son rectas que no pasan por el origen, cortando el eje y en el punto (0,n). Ninguna de estas tres tiene máximos ni mínimos porque son líneas rectas.

Las funciones cuadráticas f $x$ = ax² + bx + c son parábolas que siempre debes saber analizar. Si a > 0, la parábola "sonríe" (cóncava hacia arriba) y tiene un mínimo; si a < 0, "está triste" (cóncava hacia abajo) y tiene un máximo.

Para encontrar el vértice de una parábola, usa la fórmula x = -b/(2a) y después calcula y sustituyendo este valor. Las funciones de proporcionalidad inversa f $x$ = k/x forman hipérbolas que nunca tocan los ejes y tienen comportamientos opuestos según el signo de k.

Consejo de examen: Las funciones cuadráticas aparecen constantemente en problemas. Memoriza la fórmula del vértice y practica encontrar puntos de corte factorizando o usando la fórmula cuadrática.

Funciones, límites y continuidad – página 3

Inscríbete para ver los apuntes.
¡Es gratis!

Funciones Especiales: Exponenciales, Logarítmicas y Trigonométricas

Las funciones logarítmicas f $x$ = log x solo existen para valores positivos de x (dominio: x > 0) y siempre cortan el eje x en (1,0). Son crecientes si la base es mayor que 1 y decrecientes si es menor.

Las funciones exponenciales f $x$ = aˣ tienen dominio infinito pero nunca tocan el eje x, cortando siempre el eje y en (0,1). Su crecimiento depende de si la base es mayor o menor que 1.

Las funciones radicales f $x$ = ⁿ√x cambian su dominio según si el índice es par o impar. Con índice par necesitas que el radicando sea no negativo; con índice impar el dominio es todo ℝ.

Las funciones trigonométricas son periódicas y acotadas. La función seno tiene simetría impar (sen $-x$ = -sen x) mientras que el coseno tiene simetría par (cos $-x$ = cos x). Ambas oscilan entre -1 y 1, repitiéndose cada 2π.

Dato importante: Las funciones exponenciales crecen muchísimo más rápido que las polinómicas. Esta diferencia es crucial para entender límites al infinito.

Funciones, límites y continuidad – página 4

Inscríbete para ver los apuntes.
¡Es gratis!

Funciones a Trozos y Valor Absoluto

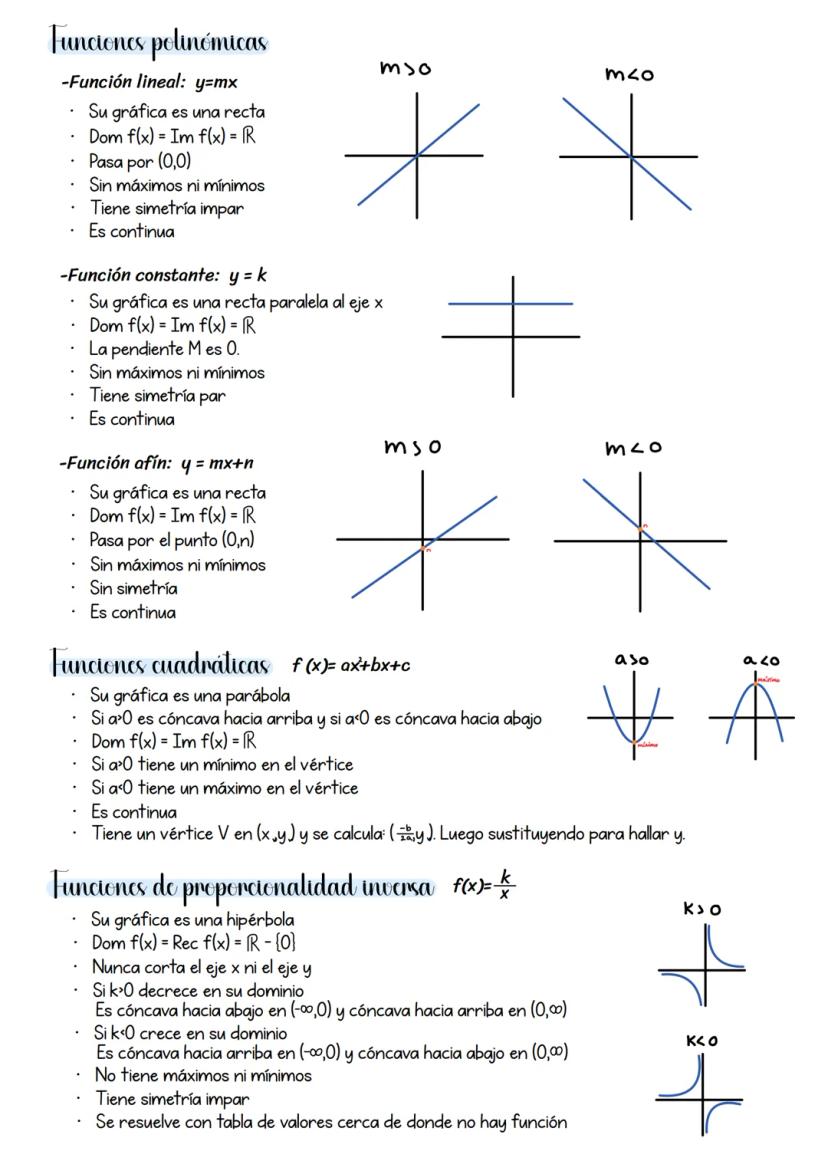
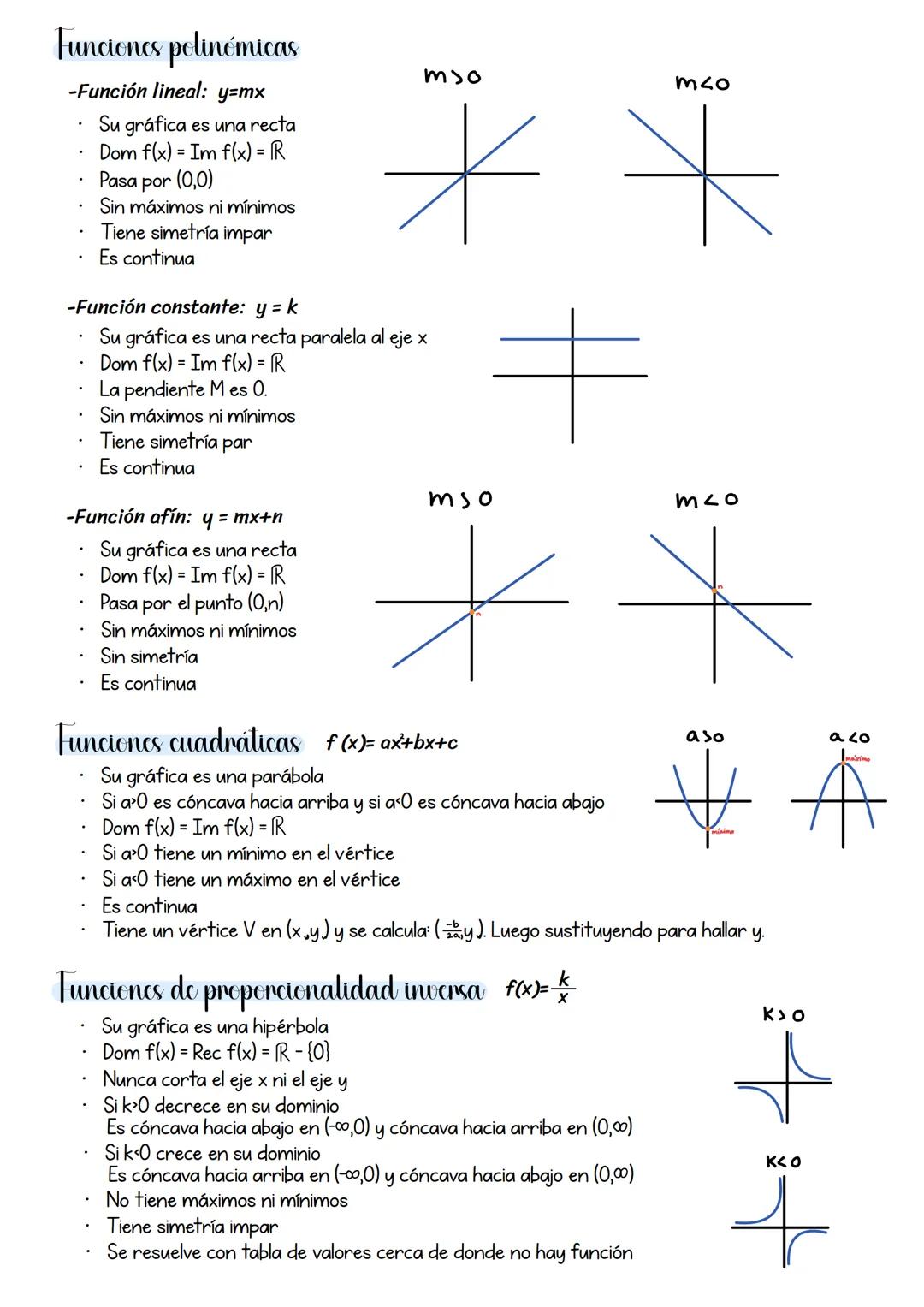
Las funciones a trozos combinan diferentes tipos de funciones en distintos intervalos. Para representarlas, analiza cada trozo por separado y luego únelos respetando los intervalos dados.

Cuando trabajas con funciones de valor absoluto como f $x$ = |x + 1|, el proceso tiene cuatro pasos clave: encuentra dónde se anula la expresión dentro del valor absoluto, estudia los signos en cada intervalo, reescribe la función como función a trozos, y representa cada parte por separado.

El valor absoluto convierte todos los valores negativos en positivos, creando esa característica forma de "V". Para f $x$ = |x + 1|, la función se anula cuando x = -1, dividiendo el dominio en dos partes.

En el intervalo donde x < -1, la expresión x + 1 es negativa, así que |x + 1| = - $x + 1$ . En el intervalo donde x ≥ -1, la expresión es positiva, así que |x + 1| = x + 1.

Estrategia de resolución: Siempre empieza encontrando los "puntos críticos" donde la expresión dentro del valor absoluto se hace cero. Estos puntos dividen tu función en trozos más manejables.

Funciones, límites y continuidad – página 5

Inscríbete para ver los apuntes.
¡Es gratis!

Dominios y Representación de Funciones

Calcular el dominio es fundamental y sigue reglas claras según el tipo de función. Los polinomios siempre tienen dominio ℝ, mientras que los cocientes excluyen los valores que anulan el denominador.

Para las raíces, si el índice es impar el dominio es ℝ, pero si es par necesitas que el radicando sea ≥ 0. En logaritmos, el argumento debe ser estrictamente positivo.

Los límites estudian el comportamiento de una función cuando x se aproxima a un valor determinado. Puedes calcularlo mediante tablas de valores, tomando números cada vez más cercanos al punto de interés.

Desde una gráfica, el límite existe si al aproximarte al punto desde ambos lados llegas al mismo valor y. No importa si existe o no la función en ese punto exacto; lo que cuenta es hacia dónde "tiende".

Técnica de estudio: Para representar cualquier función necesitas dominio, puntos de corte con los ejes, tabla de valores y características especiales como vértices en parábolas.

Funciones, límites y continuidad – página 6

Inscríbete para ver los apuntes.
¡Es gratis!

Límites Laterales y Operaciones

Los límites laterales son cruciales cuando la función se comporta de forma diferente al aproximarse por la izquierda (x → a⁻) o por la derecha (x → a⁺). El límite solo existe si ambos laterales coinciden.

Los límites infinitos aparecen cuando la función crece o decrece sin límite al acercarse a un punto. Se identifican fácilmente en las gráficas como asíntotas verticales.

Para el cálculo práctico de límites, simplemente sustituye el valor de x. Si obtienes un resultado numérico, ese es tu límite. El problema surge con las indeterminaciones.

Las operaciones con límites siguen las reglas aritméticas habituales: puedes sumar, restar, multiplicar y dividir límites, siempre que estos existan y no generen indeterminaciones.

Regla de oro: Si al sustituir directamente obtienes un número, ese es tu límite. Las complicaciones solo aparecen con las formas indeterminadas como 0/0 o ∞/∞.

Funciones, límites y continuidad – página 7

Inscríbete para ver los apuntes.
¡Es gratis!

Indeterminaciones: Resolviendo lo Imposible

Las indeterminaciones son situaciones donde la sustitución directa no funciona. Cada tipo tiene su estrategia específica de resolución.

La indeterminación k/0 siempre da ±∞. Para determinar el signo, estudia los límites laterales observando si el denominador se acerca a cero por valores positivos o negativos.

La indeterminación 0/0 se resuelve factorizando numerador y denominador, cancelando factores comunes. En funciones racionales, esto suele implicar encontrar las raíces que anulan ambas partes.

La indeterminación ∞/∞ en funciones racionales se resuelve dividiendo por la x de mayor exponente, o más rápido: si el grado del numerador es mayor que el denominador, el límite es ±∞; si es menor, es 0; si son iguales, es el cociente de los coeficientes principales.

Truco para ∞ - ∞: Cuando tengas raíces, multiplica y divide por el conjugado. Esto transformará la indeterminación en una forma manejable como ∞/∞ o 0/0.

Funciones, límites y continuidad – página 8

Inscríbete para ver los apuntes.
¡Es gratis!

Continuidad: Cuando las Funciones Fluyen Sin Interrupciones

Una función es continua en x = a si cumple tres condiciones: existe f $a$ , existe el límite cuando x tiende a a, y ambos valores coinciden. Si falla alguna, hay discontinuidad.

Las discontinuidades evitables ocurren cuando el límite existe pero no coincide con f $a$ , o cuando f $a$ no existe pero el límite sí. Son "reparables" redefiniendo la función en ese punto.

Las discontinuidades no evitables se clasifican en dos tipos. Las de primera especie incluyen saltos finitos (límites laterales diferentes) y saltos infinitos (al menos un límite lateral es infinito).

Las discontinuidades de segunda especie son las más complicadas: no existe al menos uno de los límites laterales, creando comportamientos caóticos cerca del punto.

Método sistemático: Para estudiar continuidad, siempre verifica en este orden: ¿existe f $a$ ?, ¿existen los límites laterales?, ¿coinciden?, ¿coincide f $a$ con el límite? Cada "no" te dice qué tipo de discontinuidad tienes.

Funciones, límites y continuidad – página 9

Inscríbete para ver los apuntes.
¡Es gratis!

Pensamos que nunca lo preguntarías...

Nuestro compañero de IA está específicamente adaptado a las necesidades de los estudiantes. Basándonos en los millones de contenidos que tenemos en la plataforma, podemos dar a los estudiantes respuestas realmente significativas y relevantes. Pero no se trata solo de respuestas, el compañero también guía a los estudiantes a través de sus retos de aprendizaje diarios, con planes de aprendizaje personalizados, cuestionarios o contenidos en el chat y una personalización del 100% basada en las habilidades y el desarrollo de los estudiantes.

Puedes descargar la app en Google Play Store y Apple App Store.

Sí, tienes acceso gratuito a los contenidos de la aplicación y a nuestro compañero de IA. Para desbloquear determinadas funciones de la aplicación, puedes adquirir Knowunity Pro.

Conceptos Básicos: Funciones, Límites y Continuidad

Funciones y sus Características Básicas

Funciones Polinómicas: Las Más Frecuentes en Selectividad

Funciones Especiales: Exponenciales, Logarítmicas y Trigonométricas

Funciones a Trozos y Valor Absoluto

Dominios y Representación de Funciones

Límites Laterales y Operaciones

Indeterminaciones: Resolviendo lo Imposible

Continuidad: Cuando las Funciones Fluyen Sin Interrupciones

Pensamos que nunca lo preguntarías...

¿Qué es Knowunity AI companion?

¿Dónde puedo descargar la app Knowunity?

¿Knowunity es totalmente gratuito?

Contenido similar

Limites y continuidad (análisis)

Matemáticas 2 bachillerato ciencias sociales

Funciones

FUNCIONES Y DERIVADAS

Intervalos y semirectas .

Control

Contenidos más populares: discontinuidad removible

Matemáticas 2 bachillerato ciencias sociales

FUNCIONES Y DERIVADAS

Limites y continuidad (análisis)

Contenidos más populares: Matemáticas

MATEMÁTICAS I

Trigonometría

MATES CIENCIAS 1 BACHILLERATO

Matemáticas II (análisis) 2Bach

Matemática todo el curso

Matemáticas 2 Bachillerato completo (con probabilidad)

Potencias

Trigonométria 1 bach

Funciones

Contenidos más populares

Carnet Conducir

Apuntes teorico carnet de conducir ACTUALIZADO

Apuntes examen teórico de coche

Apuntes Teorico Permiso B

Resumen completo carnet de conducir B – Esquemas y teoría explicada (40 pág)

INGLÉS B1 (Cambridge)

Teórico Coche B 2026

Inglés B2 (Parte 1)

Tiempos verbales en inglés

Mira lo que dicen nuestros usuarios. Les encanta - y a tí también.