Resolviendo funciones afines complejas
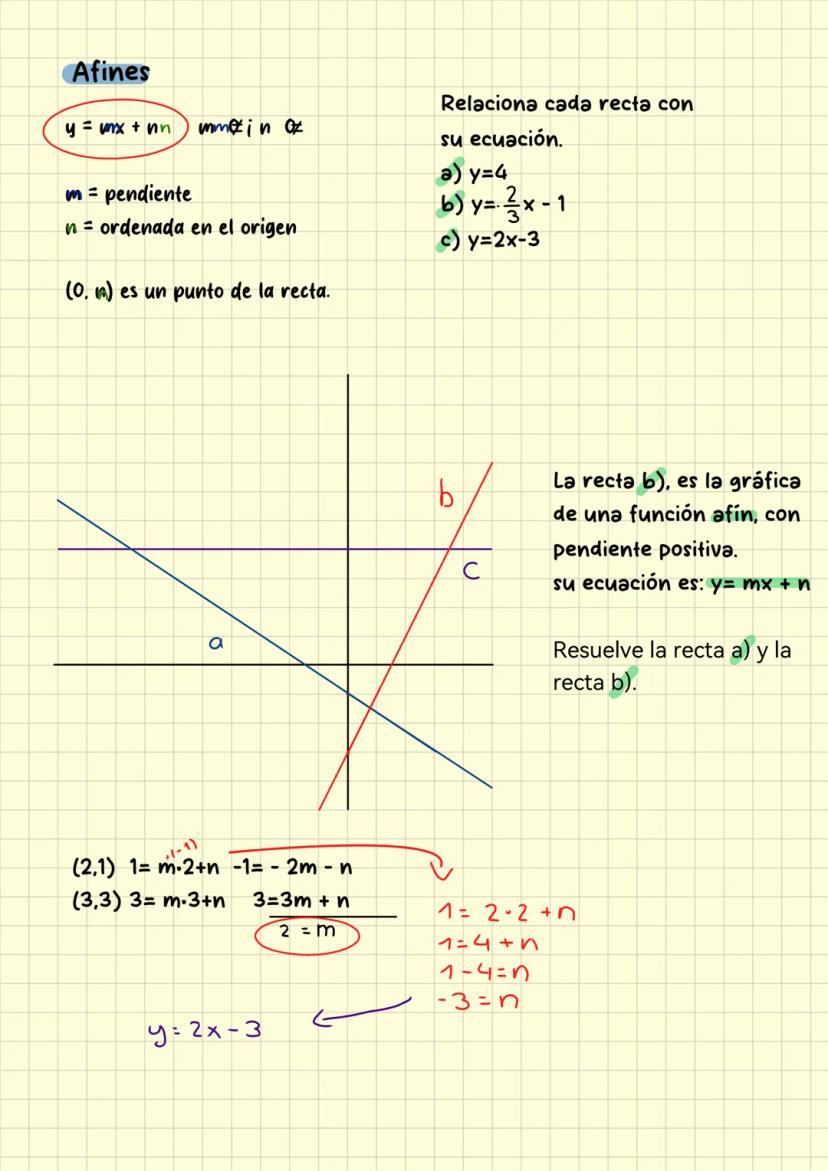
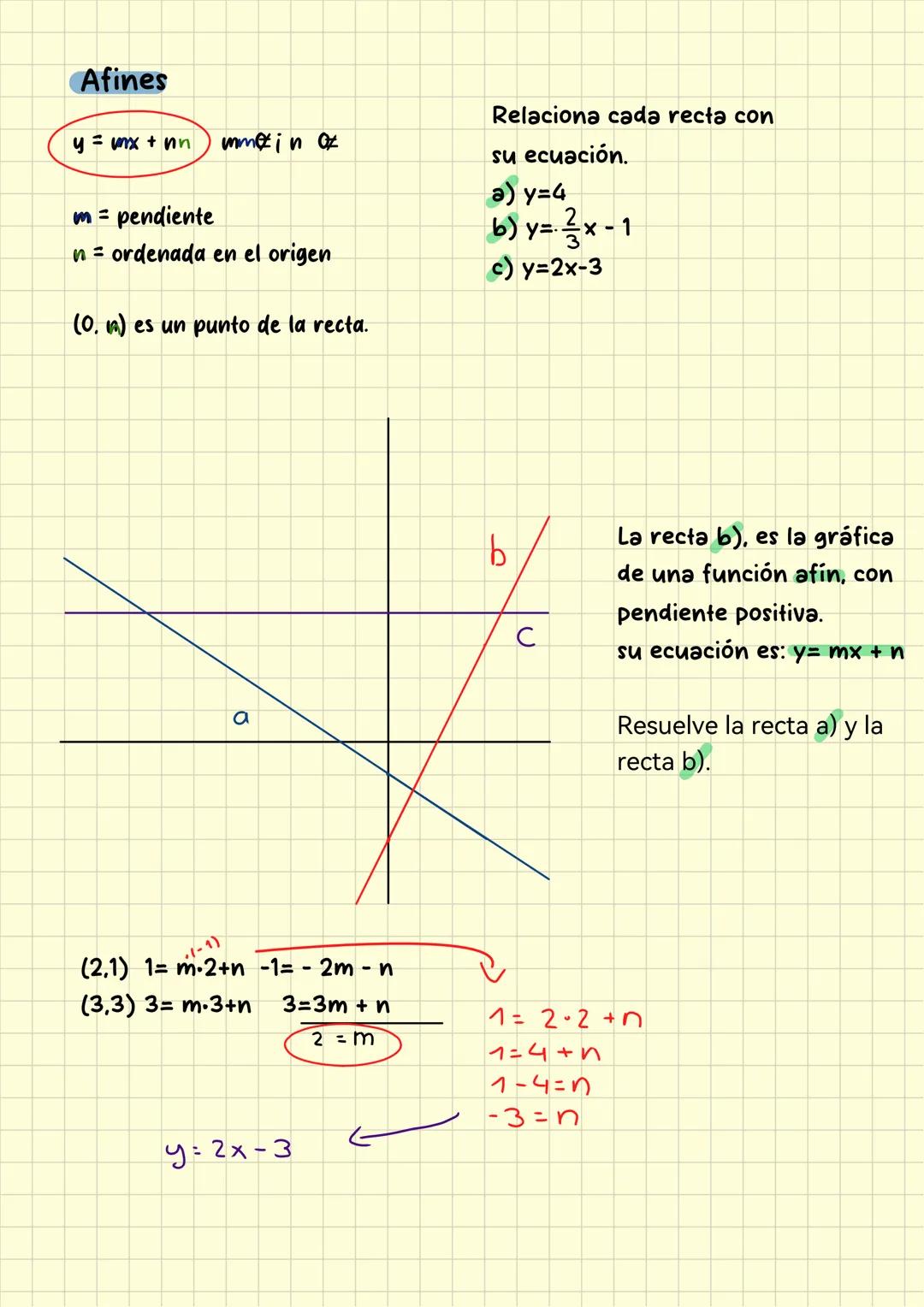
Aquí viene lo emocionante: resolver sistemas de ecuaciones para encontrar funciones afines. Cuando tienes dos puntos, como (-9,5) y (-3,1), puedes encontrar tanto la pendiente como la ordenada.
Primero calcula la pendiente: m = (1-5)/(-3-(-9)) = -4/6 = -2/3. Luego sustituye en cualquier punto para encontrar n. Con 1,−3×(−2/3)+n, obtienes n = -1.
La función completa es y = -2/3x - 1. ¡Siempre verifica con ambos puntos para estar seguro!
Las funciones constantes son más simples: si todos los puntos tienen la misma coordenada Y, como (0,4), entonces y = 4 sin importar el valor de x.
Truco de experto: Si la pendiente te sale con decimales complicados, conviértela a fracción. Es más fácil trabajar con fracciones en estos problemas.