Matemáticas

Continuidad y Discontinuidades de Funciones

discontinuidad

Matemáticas815Actualizado 4 sept 202611 páginas

Conceptos Clave: Funciones, Límites y Discontinuidades

Denunciar

Eva Corralejo Sanchez@evacosan333

Añadir a fuentes de Google

Las funciones, límites y discontinuidades son conceptos fundamentales en matemáticas que te ayudarán a entender cómo se comportan las gráficas y resolver problemas complejos. Estos temas son la base del análisis matemático y aparecerán constantemente en selectividad.

Funciones limites y discontinuidades – página 1

Inscríbete para ver los apuntes.
¡Es gratis!

Concepto y Definición de una Función

¿Sabías que las funciones están por todas partes? Desde el precio de la gasolina hasta tu velocidad en bici, todo son funciones relacionando variables.

Una función es simplemente una relación entre dos variables donde a cada valor de x le corresponde un único valor de y. El dominio son todos los valores posibles de x, y el recorrido son todos los valores posibles de y.

Para calcular el dominio, recuerda estas reglas clave: las funciones polinómicas tienen dominio ℝ completo, las funciones racionales excluyen valores que anulen el denominador, y las funciones radicales con índice par necesitan que lo de dentro de la raíz sea ≥ 0.

Truco clave: En funciones racionales como f $x$ = 1/ $x-6$ , busca siempre qué valores hacen cero el denominador. Esos valores NO pertenecen al dominio.

Funciones limites y discontinuidades – página 2

Inscríbete para ver los apuntes.
¡Es gratis!

Formas de Definir y Representar Funciones

Las funciones se pueden expresar de varias formas: mediante enunciados, tablas de valores, ecuaciones o gráficas. La más útil para ti será dominar las funciones definidas a trozos.

Las funciones definidas a trozos son como tener varias "mini-funciones" que actúan en diferentes intervalos. Por ejemplo, una función puede comportarse como x+1 cuando x>1, pero como x²+2 cuando x≤0.

Para representar estas funciones, trabaja por partes: dibuja cada trozo en su intervalo correspondiente y presta atención a los puntos de "cambio". Estos puntos suelen ser donde la función puede presentar discontinuidades.

Consejo: Al representar funciones a trozos, marca siempre con círculos abiertos (○) o cerrados (●) los extremos de cada intervalo según corresponda.

Funciones limites y discontinuidades – página 3

Inscríbete para ver los apuntes.
¡Es gratis!

Operaciones con Funciones

Trabajar con funciones es como manejar piezas de LEGO: puedes combinarlas para crear algo más complejo. Las operaciones básicas son suma, producto y cociente de funciones.

La composición de funciones (f∘g) es especialmente importante: significa aplicar primero g y luego f al resultado. El dominio de f∘g incluye solo los valores donde ambas operaciones son válidas.

Las funciones inversas son como "deshacer" una función. No todas las funciones tienen inversa, solo las inyectivas (donde cada valor de y corresponde a un único x). Para calcular f⁻¹, intercambia variables y despeja y.

Recordatorio: La composición NO es conmutativa: (f∘g) $x$ ≠ (g∘f) $x$ en general.

Funciones limites y discontinuidades – página 4

Inscríbete para ver los apuntes.
¡Es gratis!

Límites: Definición y Tipos

Los límites te dicen hacia dónde "se dirige" una función cuando x se acerca a un valor determinado. Es como predecir el comportamiento de la función sin necesidad de evaluarla exactamente en ese punto.

La notación lim_{x→a} f $x$ = L significa que cuando x se aproxima a 'a', f $x$ se aproxima a L. Pueden existir límites laterales diferentes: por la izquierda (x→a⁻) y por la derecha (x→a⁺).

Los límites infinitos aparecen cuando la función crece o decrece sin límite. Esto suele ocurrir cerca de las asíntotas verticales, donde el denominador de una fracción se hace cero.

Importante: Para que exista el límite en un punto, los límites laterales deben coincidir.

Funciones limites y discontinuidades – página 5

Inscríbete para ver los apuntes.
¡Es gratis!

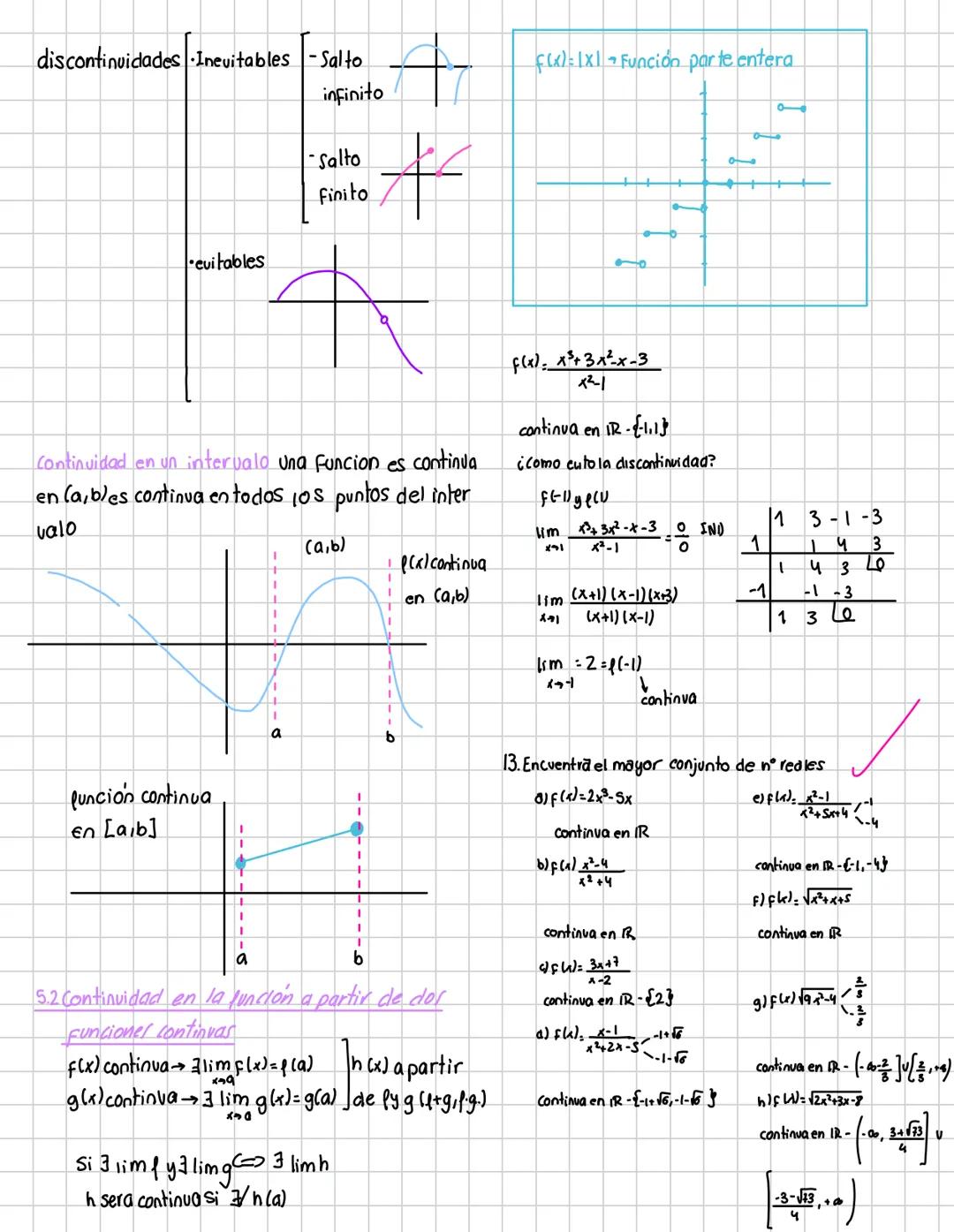
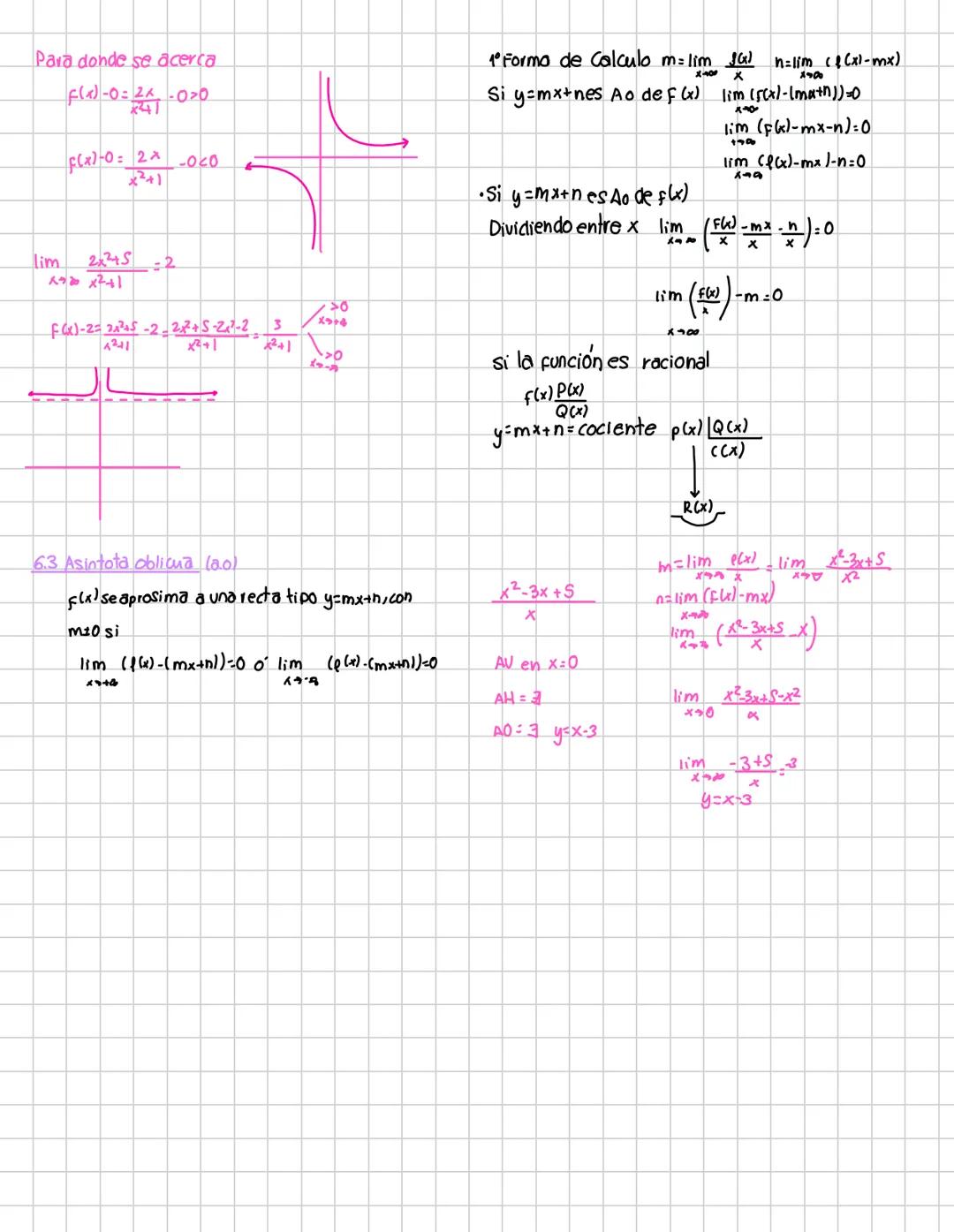
Cálculo de Límites e Indeterminaciones

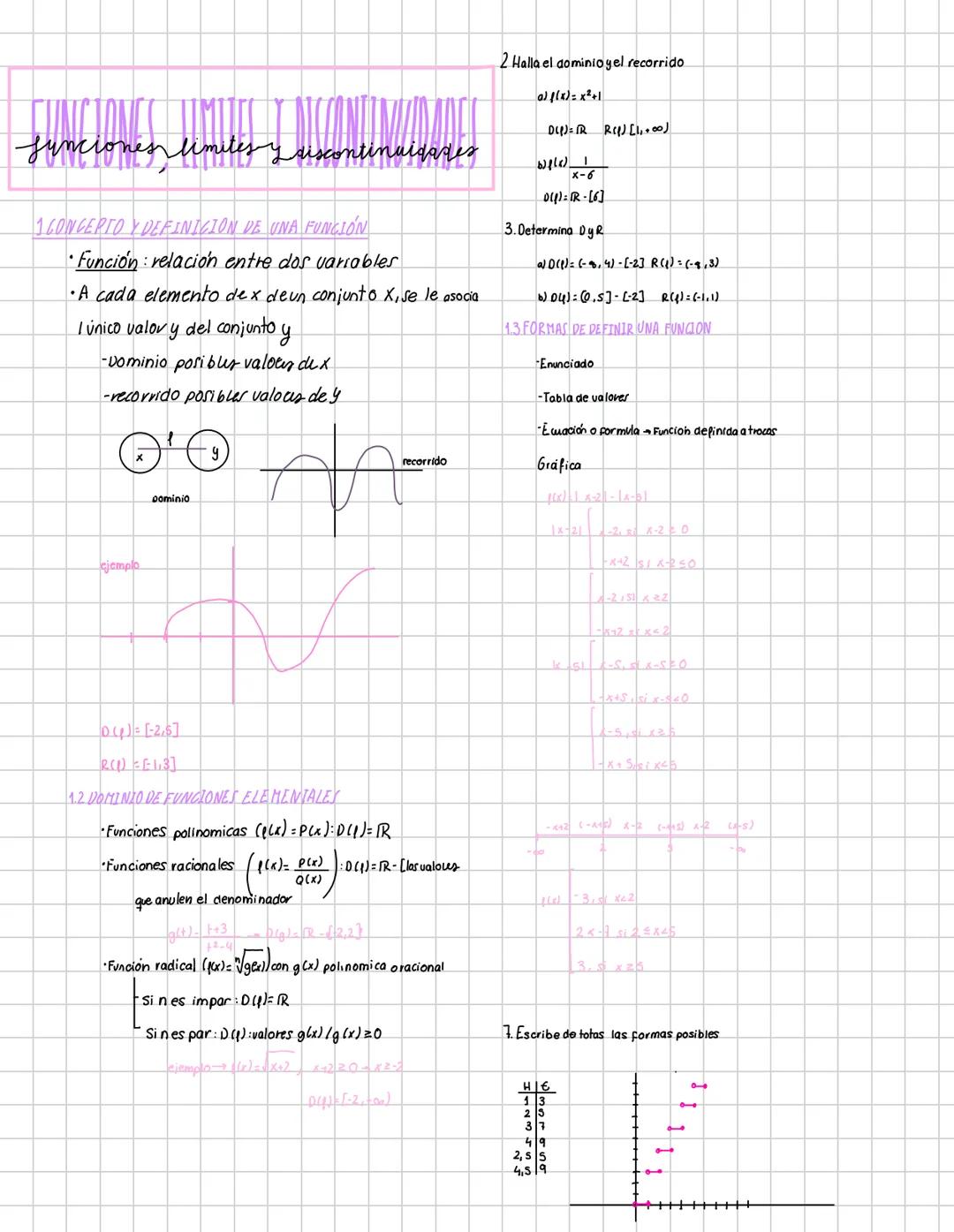
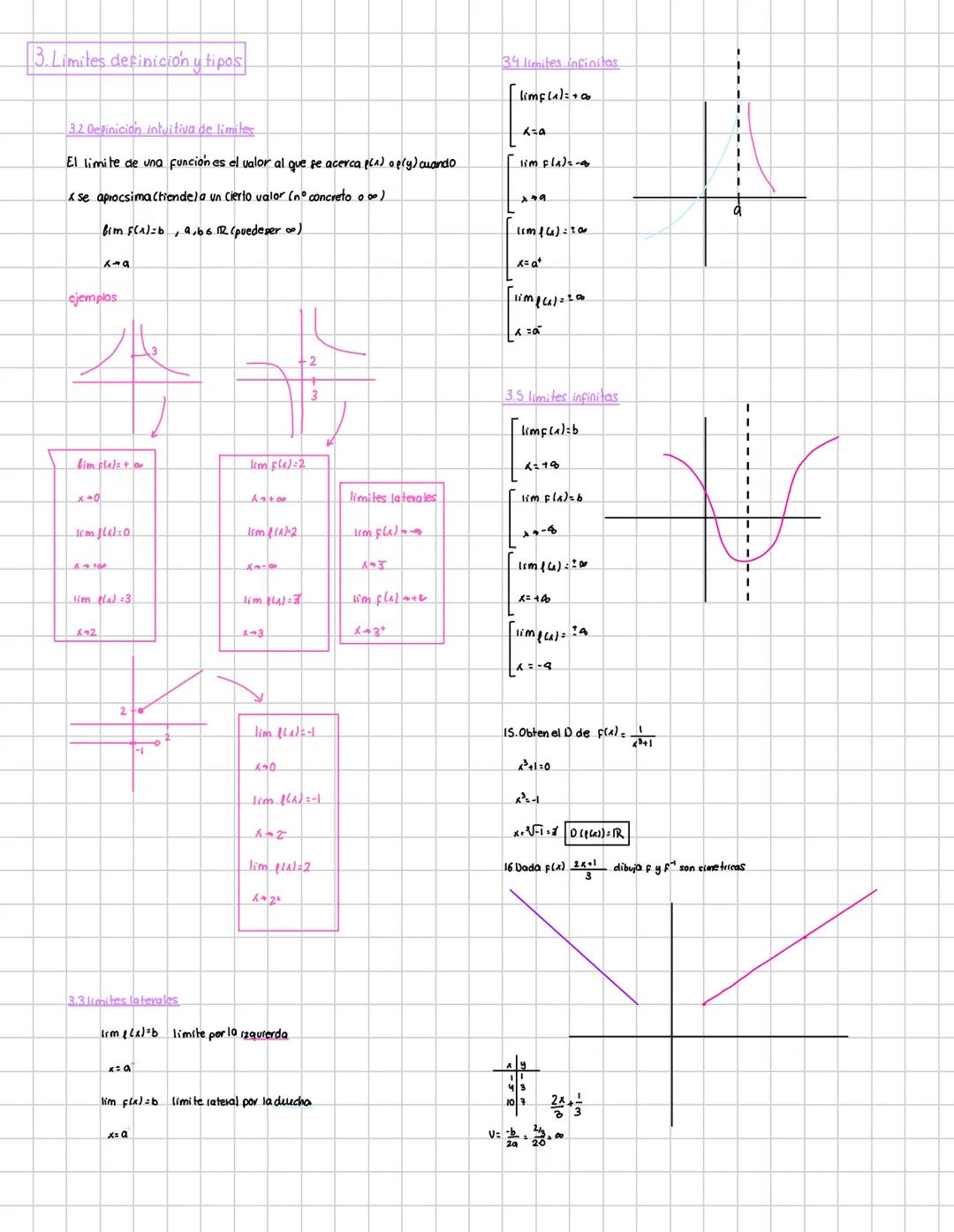
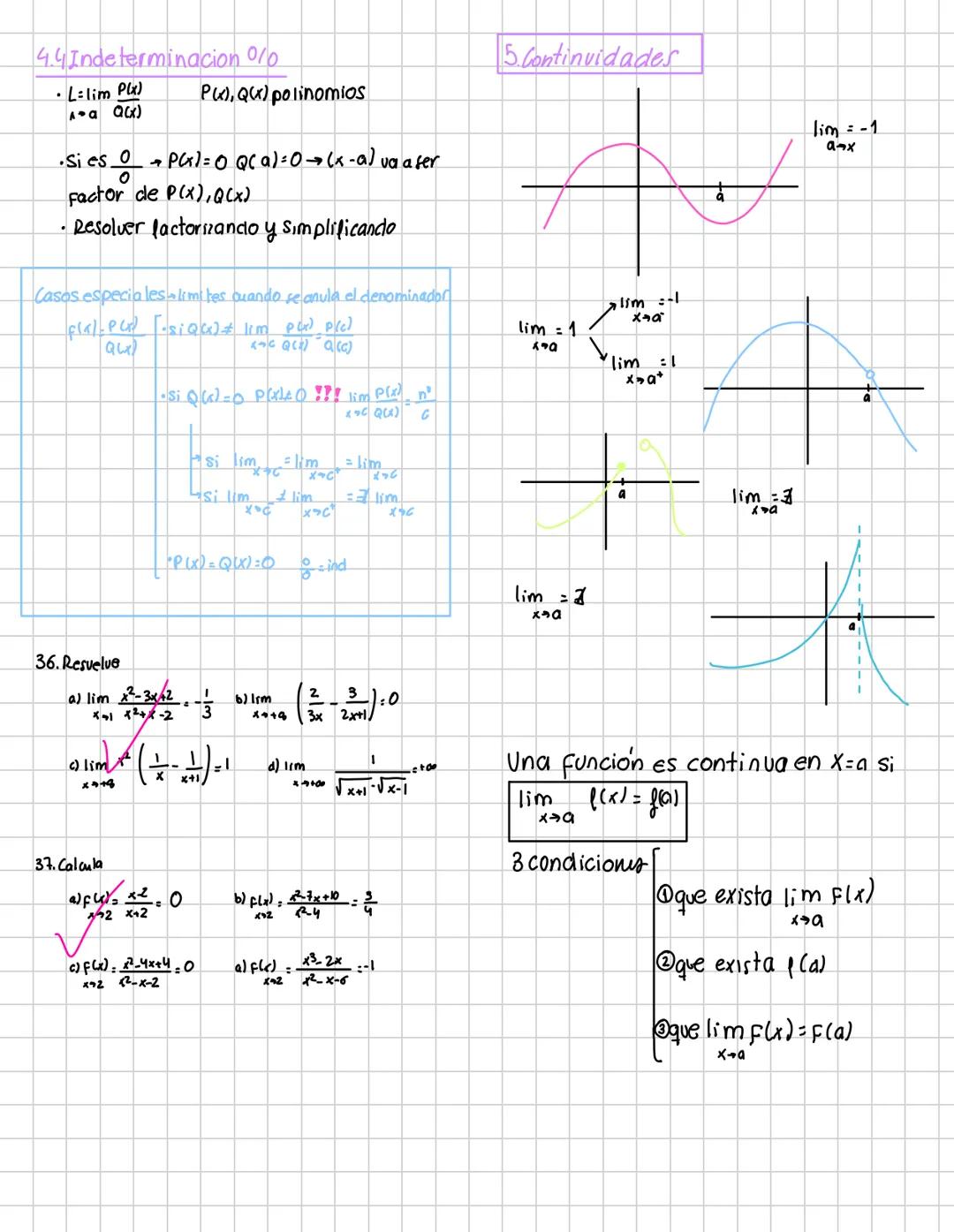
Calcular límites es más fácil de lo que parece si sigues un método ordenado. Primero, intenta sustituir directamente el valor. Si obtienes un número real, ¡ya tienes la respuesta!

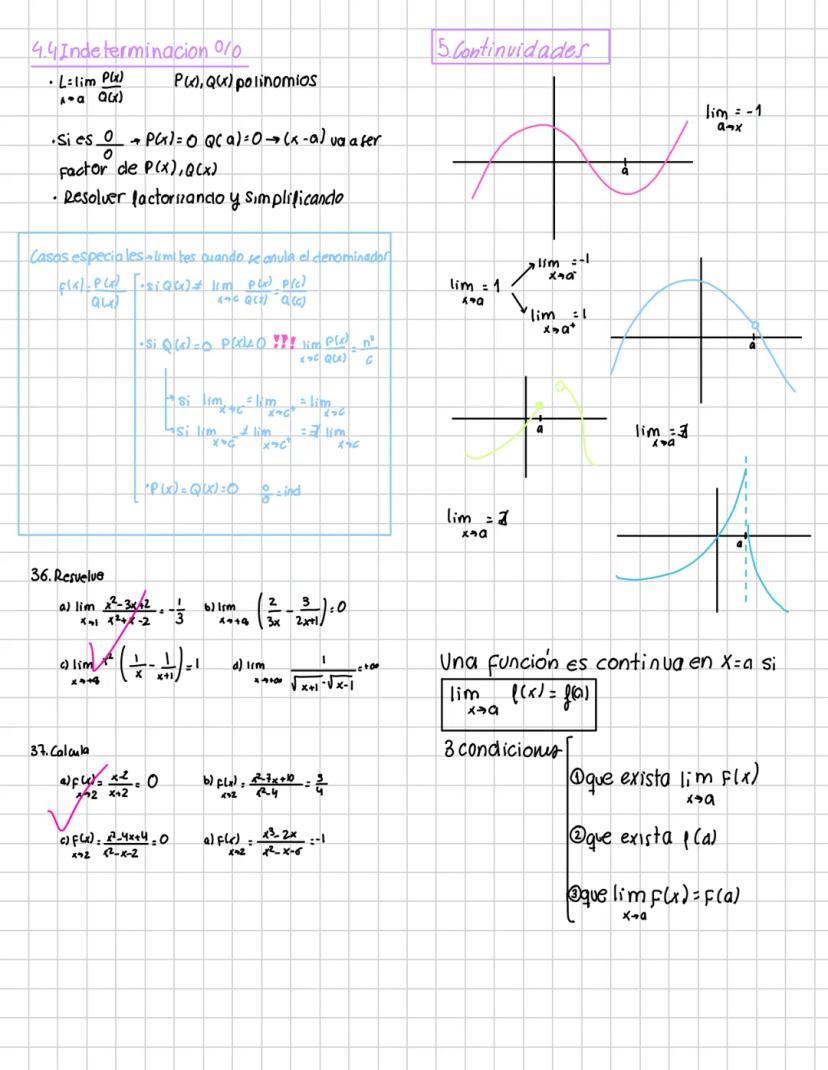
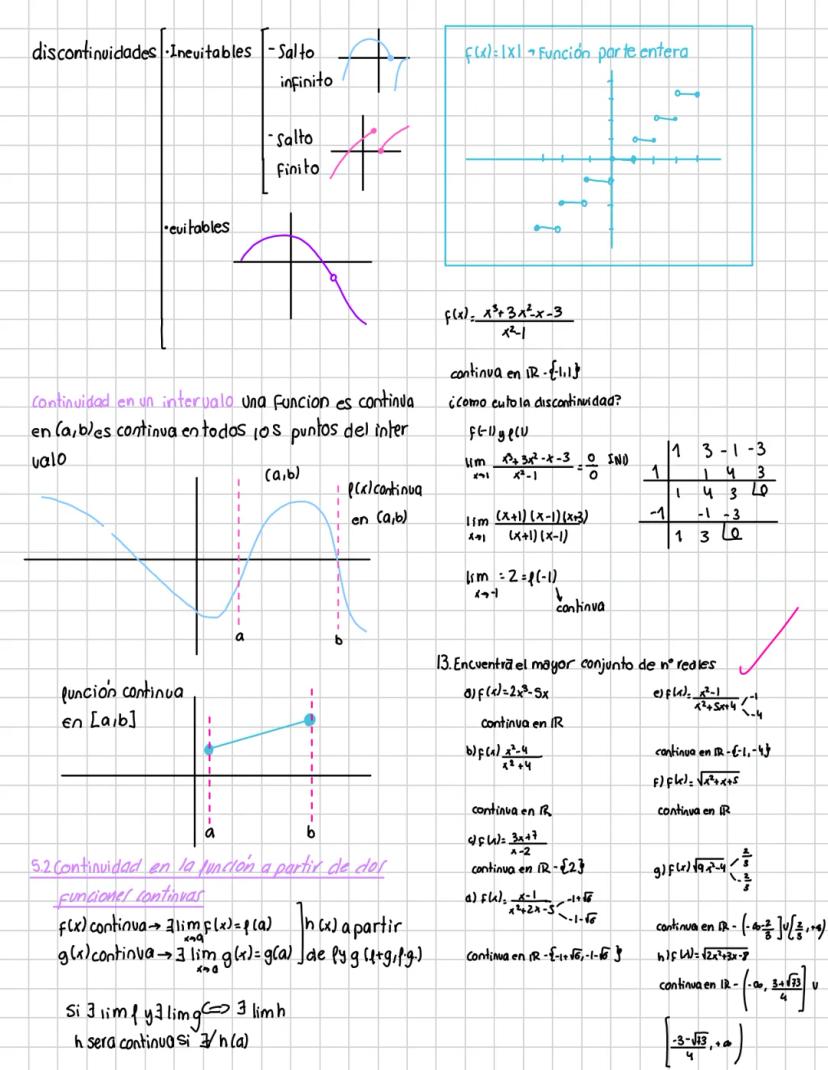
Cuando la sustitución directa no funciona, aparecen las indeterminaciones: 0/0, ∞/∞, 0·∞, ∞-∞, etc. Estas requieren técnicas especiales para resolverse.

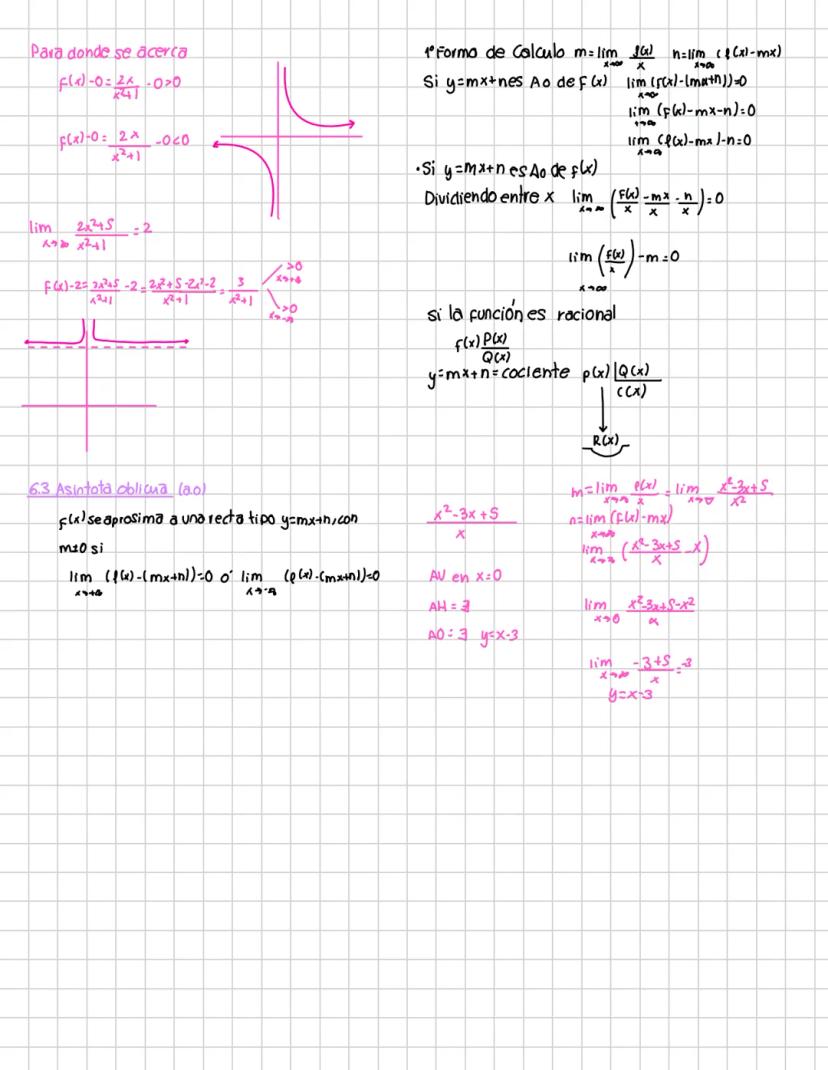
Las propiedades de los límites te permiten operar con ellos: el límite de una suma es la suma de los límites, el límite de un producto es el producto de los límites, etc. Pero cuidado: estas reglas solo funcionan cuando los límites individuales existen y son finitos.

Estrategia: Si encuentras una indeterminación, no te asustes. Es simplemente una señal de que necesitas usar alguna técnica especial para resolver el límite.

Funciones limites y discontinuidades – página 6

Inscríbete para ver los apuntes.
¡Es gratis!

Resolución de Indeterminaciones

Las indeterminaciones del tipo 0/0 son las más frecuentes en bachillerato. Cuando tanto numerador como denominador se anulan, significa que $x-a$ es factor común de ambos.

Para resolverlas, factoriza numerador y denominador, simplifica los factores comunes y vuelve a intentar el límite. Otra opción es usar la Regla de L'Hôpital: deriva numerador y denominador por separado.

Las indeterminaciones tipo ∞/∞ se resuelven dividiendo numerador y denominador por la mayor potencia de x que aparezca. Las de tipo ∞-∞ requieren técnicas como sacar factor común o racionalizar.

Técnica clave: En fracciones con radicales, multiplica y divide por el conjugado para eliminar la indeterminación.

Funciones limites y discontinuidades – página 7

Inscríbete para ver los apuntes.
¡Es gratis!

Continuidad de Funciones

Una función es continua en x=a si puedes dibujarla sin levantar el lápiz del papel en ese punto. Matemáticamente, necesitas tres condiciones: que exista f $a$ , que exista lim_{x→a} f $x$ , y que ambos sean iguales.

Las discontinuidades se clasifican en evitables (un "agujero" que se puede "tapar") e inevitables (saltos finitos o infinitos). Las funciones polinómicas son siempre continuas en todo ℝ.

Para estudiar la continuidad en funciones definidas a trozos, examina los puntos donde cambia la definición. Calcula los límites laterales y compáralos con el valor de la función en ese punto.

Consejo práctico: Si una función racional tiene el mismo factor en numerador y denominador, presenta una discontinuidad evitable.

Funciones limites y discontinuidades – página 8

Inscríbete para ver los apuntes.
¡Es gratis!

Tipos de Discontinuidades y Continuidad Global

Las discontinuidades inevitables se dividen en salto finito (la función "salta" a otro valor) y salto infinito (la función tiende a ±∞). Las evitables son "agujeros" que podrían rellenarse redefiniendo la función.

Una función es continua en un intervalo si es continua en todos los puntos de ese intervalo. Las funciones racionales son continuas en ℝ excepto donde se anula el denominador.

Para funciones con radicales de índice par, el dominio se restringe a donde el radicando es no negativo, y en ese dominio la función es continua.

Regla útil: Si tienes dos funciones continuas, cualquier combinación (suma, producto, cociente) también será continua donde esté definida.

Funciones limites y discontinuidades – página 9

Inscríbete para ver los apuntes.
¡Es gratis!

Asíntotas Verticales y Horizontales

Las asíntotas verticales son rectas x=a hacia las que se acerca la gráfica cuando la función tiende a ±∞. En funciones racionales, búscalas donde se anula el denominador pero no el numerador.

Las asíntotas horizontales y=L aparecen cuando lim_{x→±∞} f $x$ = L. En funciones racionales, compara los grados del numerador y denominador: si el grado del numerador es menor, AH es y=0.

Para saber si la función se acerca a la asíntota horizontal por arriba o por abajo, estudia el signo de f $x$ - L para valores grandes de x.

Truco: En funciones racionales, si los grados son iguales, la AH es y = (coeficiente líder del numerador)/(coeficiente líder del denominador).

Funciones limites y discontinuidades – página 10

Inscríbete para ver los apuntes.
¡Es gratis!

Asíntotas Oblicuas

Las asíntotas oblicuas y=mx+n aparecen cuando la función se aproxima a una recta no horizontal ni vertical. Son típicas cuando el grado del numerador supera en 1 al del denominador.

Para calcularlas, usa las fórmulas: m = lim_{x→∞} f $x$ /x y n = lim_{x→∞} $f(x) - mx$ . Si alguno de estos límites no existe o no es finito, no hay asíntota oblicua.

En funciones racionales, las asíntotas oblicuas coinciden con el cociente de la división del numerador entre el denominador. Una función no puede tener simultáneamente asíntota horizontal y oblicua.

Importante: Las asíntotas oblicuas y horizontales son excluyentes. Si existe una, no puede existir la otra.

Pensamos que nunca lo preguntarías...

Nuestro compañero de IA está específicamente adaptado a las necesidades de los estudiantes. Basándonos en los millones de contenidos que tenemos en la plataforma, podemos dar a los estudiantes respuestas realmente significativas y relevantes. Pero no se trata solo de respuestas, el compañero también guía a los estudiantes a través de sus retos de aprendizaje diarios, con planes de aprendizaje personalizados, cuestionarios o contenidos en el chat y una personalización del 100% basada en las habilidades y el desarrollo de los estudiantes.

Puedes descargar la app en Google Play Store y Apple App Store.

Sí, tienes acceso gratuito a los contenidos de la aplicación y a nuestro compañero de IA. Para desbloquear determinadas funciones de la aplicación, puedes adquirir Knowunity Pro.

Conceptos Clave: Funciones, Límites y Discontinuidades

Concepto y Definición de una Función

Formas de Definir y Representar Funciones

Operaciones con Funciones

Límites: Definición y Tipos

Cálculo de Límites e Indeterminaciones

Resolución de Indeterminaciones

Continuidad de Funciones

Tipos de Discontinuidades y Continuidad Global

Asíntotas Verticales y Horizontales

Asíntotas Oblicuas

Pensamos que nunca lo preguntarías...

¿Qué es Knowunity AI companion?

¿Dónde puedo descargar la app Knowunity?

¿Knowunity es totalmente gratuito?

Contenido similar

Intervalos

Intervalos y semirectas .

Unidad 1: Números reales 1°Bach

Intervalos y semirrectas

INTEGRACIÓN Y CÁLCULO DE ÁREAS

Control

Contenidos más populares: Matemáticas

MATEMÁTICAS I

Trigonometría

MATES CIENCIAS 1 BACHILLERATO

Matemáticas II (análisis) 2Bach

Funciones, límites y continuidad

Matemática todo el curso

Matemáticas 2 Bachillerato completo (con probabilidad)

Potencias

Trigonométria 1 bach

Contenidos más populares

Carnet Conducir

Apuntes teorico carnet de conducir ACTUALIZADO

Apuntes examen teórico de coche

Apuntes Teorico Permiso B

Resumen completo carnet de conducir B – Esquemas y teoría explicada (40 pág)

INGLÉS B1 (Cambridge)

Teórico Coche B 2026

Inglés B2 (Parte 1)

Tiempos verbales en inglés

Mira lo que dicen nuestros usuarios. Les encanta - y a tí también.