Tipos de Funciones y Propiedades Básicas

¿Alguna vez te has preguntado por qué las matemáticas parecen tan complicadas? La verdad es que las funciones son más simples de lo que piensas. Las funciones básicas como y=x, y=-x, y y=|x| son los cimientos sobre los que construirás conocimientos más complejos.

Las operaciones con funciones (suma, resta, producto, cociente y potencia) siguen reglas lógicas que ya conoces. Lo importante es aplicarlas paso a paso sin saltarte ningún cálculo.

Para encontrar los vértices de una parábola, usa las fórmulas Xv y Yv sustituyendo los valores a, b, c de tu ecuación. Los puntos de corte se calculan igualando a cero para el eje x, y sustituyendo x=0 para el eje y.

💡 Truco: Cuando te enfrentes a indeterminaciones como 0/0 o ∞/∞, siempre busca el exponente de mayor grado y divide toda la expresión entre él.

Continuidad, Límites y Análisis Completo

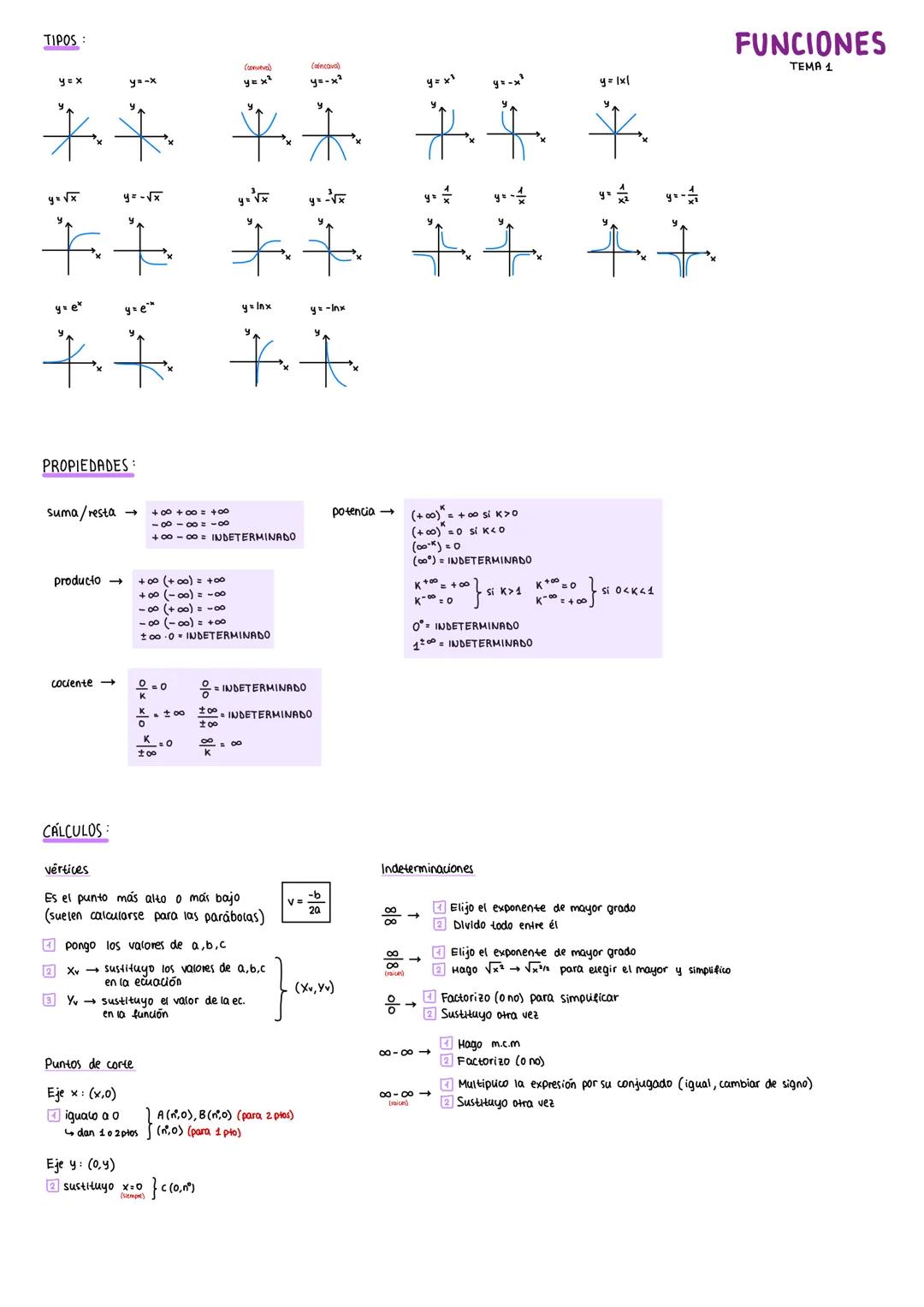
La continuidad es más fácil de entender de lo que parece: una función es continua cuando puedes dibujarla sin levantar el lápiz del papel. Para demostrarlo matemáticamente, verifica que los límites laterales coincidan y que exista f$a$.

Las discontinuidades se clasifican en evitables (cuando existe el límite pero hay un "hueco") e inevitables de primera y segunda especie. Las de primera especie tienen límites laterales distintos, mientras que en las de segunda especie no existen algunos límites.

Para las asíntotas, busca asíntotas verticales donde el denominador sea cero, y horizontales cuando x tiende a ±∞. Este análisis es crucial en funciones racionales, con raíces, logaritmos o trigonométricas.

El estudio completo incluye: tipo de función, dominio, continuidad, simetrías, asíntotas, puntos de corte y derivadas. Para las simetrías, recuerda que f$x$=f$-x$ indica función par, y f$x$=-f$-x$ función impar.

💡 Consejo: El dominio siempre excluye los valores que hacen cero al denominador. Escríbelo como Dom f$x$: ℝ - {valores problemáticos}.