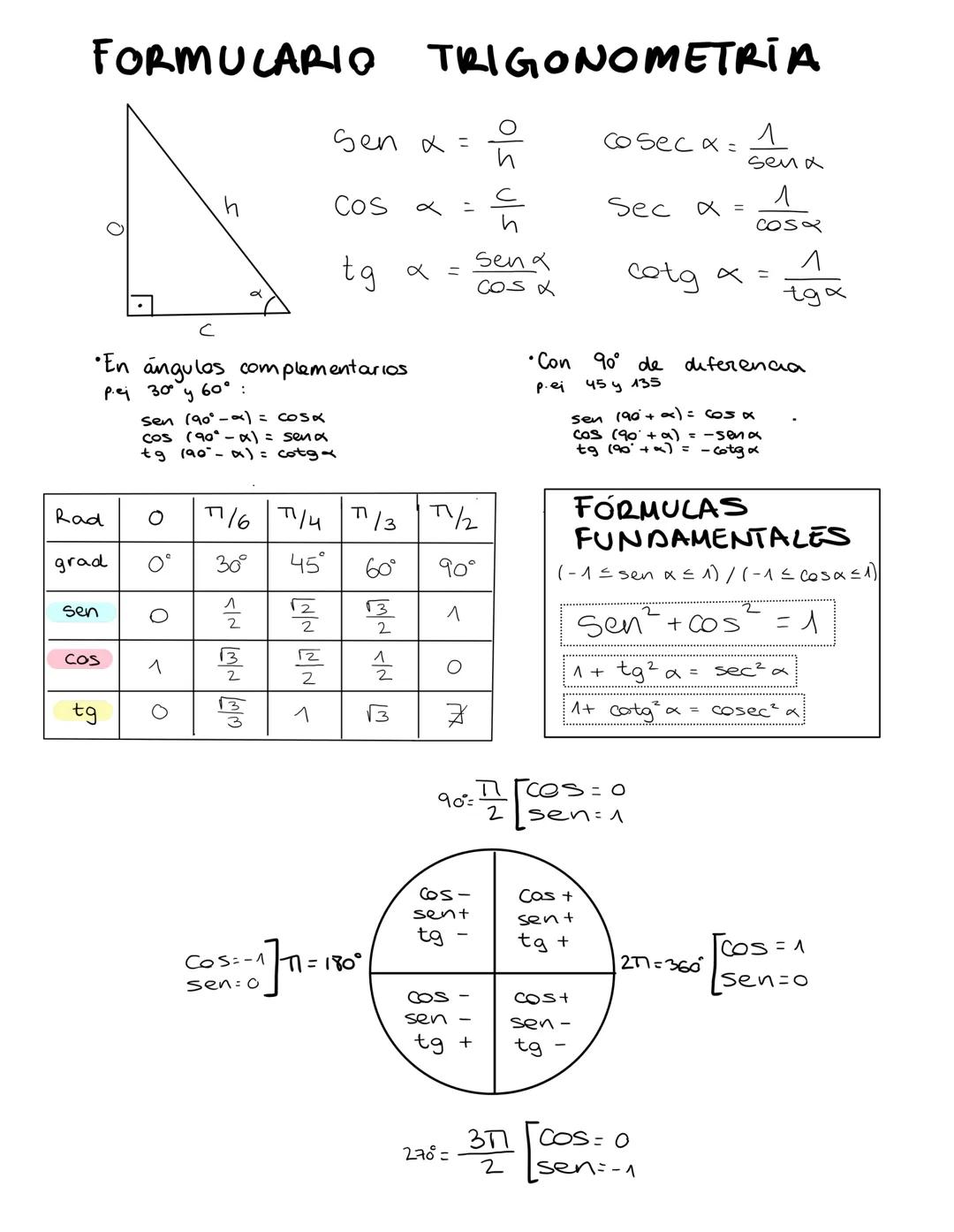
Fórmulas Trigonométricas Esenciales
Las razones de suma y resta son tu salvavidas cuando necesitas calcular senos, cosenos y tangentes de ángulos que no están en tu calculadora. Para la suma: sen(α + β) = sen α · cos β + sen β · cos α, y cos(α + β) = cos α · cos β - sen α · sen β.
Para la resta, solo cambian algunos signos: sen(α - β) = sen α · cos β - sen β · cos α, mientras que cos(α - β) = cos α · cos β + sen α · sen β. Las tangentes siguen el patrón: tg(α ± β) = (tg α ± tg β)/(1 ∓ tg α · tg β).
Las fórmulas del ángulo doble simplifican muchísimo los cálculos. Sen 2α = 2 sen α · cos α, cos 2α = cos²α - sen²α, y tg 2α = 2 tg α/1−tg2α. Son especialmente útiles en identidades y ecuaciones trigonométricas.
Truco clave: Para recordar las fórmulas de suma, piensa que el seno "suma productos cruzados" y el coseno "resta el producto de los senos".
Para el ángulo mitad, las fórmulas incluyen raíces: sen(α/2) = ±√(1−cosα)/2 y cos(α/2) = ±√(1+cosα)/2. El signo depende del cuadrante donde esté α/2.
Las fórmulas de transformación convierten sumas y restas de senos/cosenos en productos. Por ejemplo: sen A + sen B = 2 sen(A+B)/2 · cos(A−B)/2. Son geniales para simplificar expresiones complejas.
Los teoremas del seno y coseno resuelven triángulos. El teorema del seno: a/sen  = b/sen B̂ = c/sen Ĉ, y el del coseno: a² = b² + c² - 2bc · cos Â. Con estos dos, puedes resolver cualquier triángulo.