Expresiones Algebraicas y Monomios

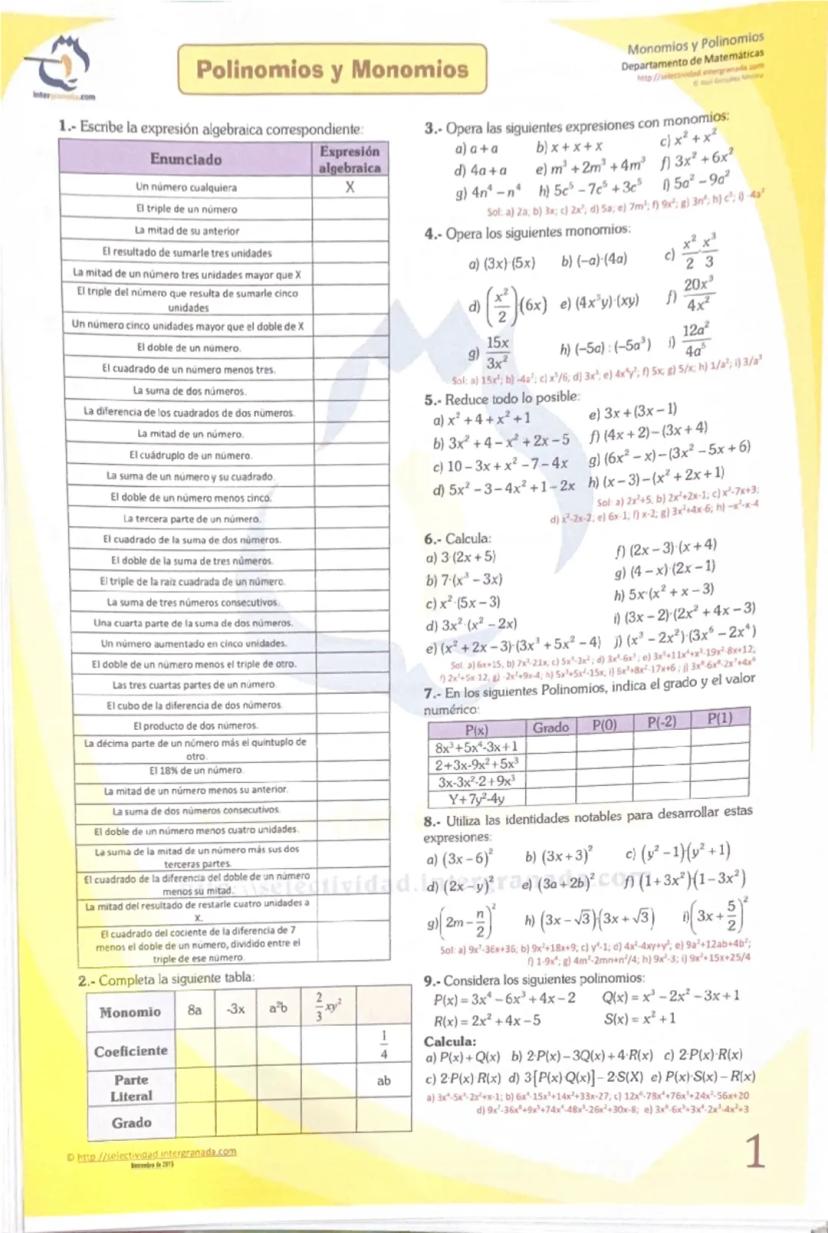
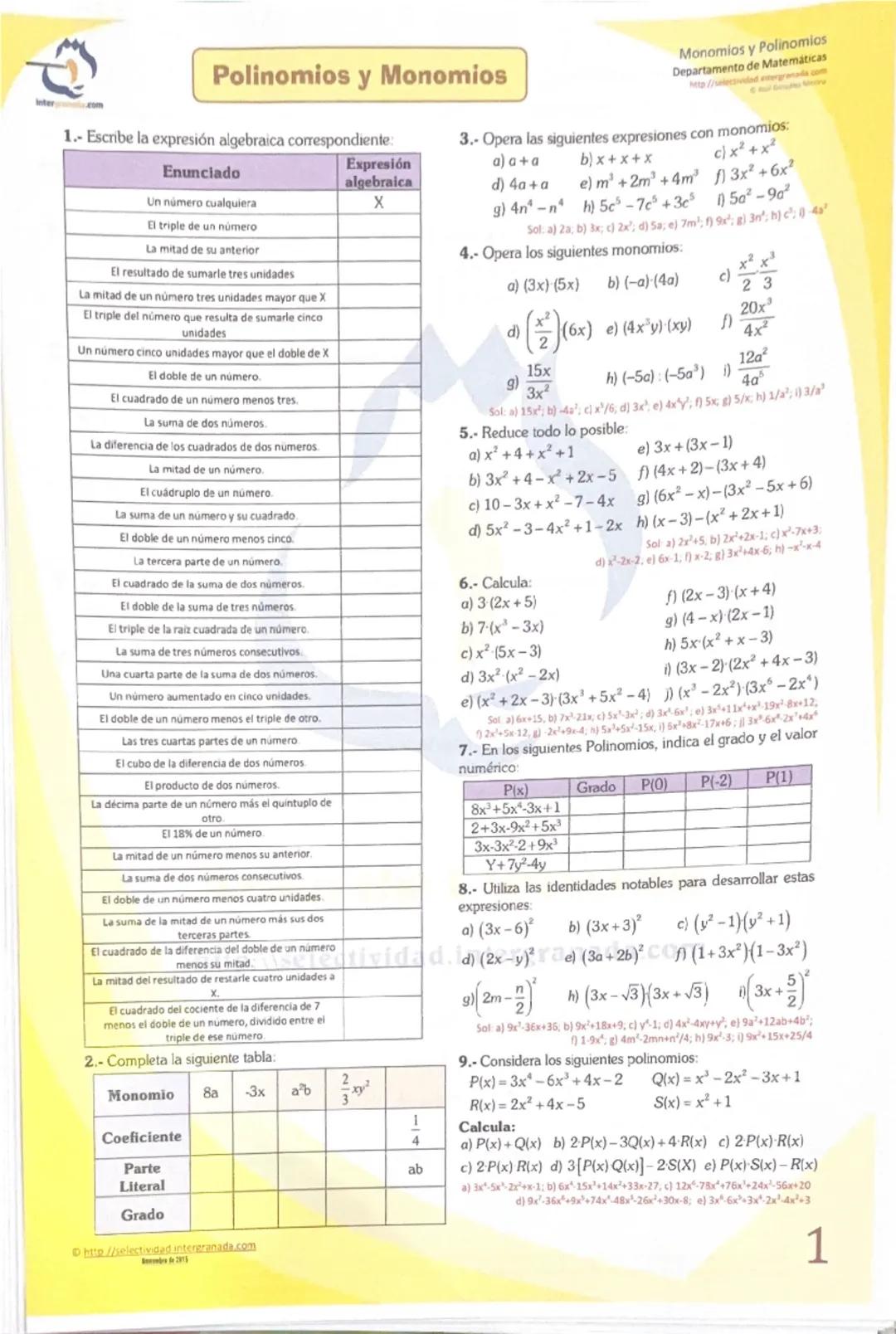
¿Sabías que puedes traducir cualquier frase del lenguaje común al lenguaje matemático? Es como aprender un nuevo idioma, pero mucho más fácil.

Una expresión algebraica es simplemente una forma de escribir con letras y números lo que dices con palabras. Por ejemplo, "el triple de un número" se escribe como 3x, donde x es tu número misterioso.

Los monomios son expresiones algebraicas de una sola pieza, como 5x² o -3xy. Tienen tres partes importantes: el coeficiente (el número de delante), la parte literal (las letras) y el grado (la suma de los exponentes).

¡Dato curioso! El grado te dice qué tan "potente" es tu monomio. Cuanto mayor sea el grado, más rápido crece el valor cuando aumentas x.

Para operar con monomios, solo puedes sumar o restar los que son semejantes (misma parte literal). Es como sumar manzanas con manzanas: 3x + 5x = 8x, pero no puedes sumar 3x + 5y directamente.

Operaciones con Monomios y Polinomios

Multiplicar y dividir monomios es más fácil de lo que parece. Solo tienes que recordar las reglas de las potencias: cuando multiplicas, sumas los exponentes, y cuando divides, los restas.

Para la multiplicación: (3x²)(5x³) = 15x⁵. Los coeficientes se multiplican (3 × 5 = 15) y los exponentes se suman (2 + 3 = 5).

Los polinomios son como familias de monomios que viven juntos. El grado del polinomio es el exponente más alto que encuentres. Para sumar polinomios, agrupas términos semejantes como si fueras organizando por colores.

¡Truco ninja! Cuando calcules el valor numérico de un polinomio, sustituye la variable por el número dado y calcula paso a paso. P(2) significa que x = 2.

El factor común es tu mejor amigo para simplificar. Es como encontrar qué tienen en común todos los términos para sacarlo fuera del paréntesis.

Productos Notables y Factorización

Los productos notables son fórmulas mágicas que te ahorran mucho tiempo. Son patrones que se repiten constantemente y que debes memorizar como una canción.

Los tres productos notables básicos son:

• Cuadrado de una suma: $a + b$² = a² + 2ab + b²
• Cuadrado de una diferencia: $a - b$² = a² - 2ab + b²
• Suma por diferencia: $a + b$$a - b$ = a² - b²

La factorización es el proceso inverso: partir una expresión en factores más simples. Es como desarmar un puzzle para ver las piezas originales.

¡Consejo de oro! Siempre busca primero el factor común antes de aplicar productos notables. Te simplificará muchísimo el trabajo.

Cuando factorices, pregúntate: "¿Qué tienen todos estos términos en común?" Puede ser un número, una letra, o ambos. Sacarlo fuera es como quitar el denominador común en las fracciones.

Operaciones Avanzadas con Polinomios

Ahora que controlas lo básico, es hora de hacer operaciones más complejas. Sumar y restar polinomios es como reorganizar tu habitación: cada cosa en su lugar.

Cuando multipliques polinomios, usa la propiedad distributiva: cada término del primer polinomio debe multiplicarse por cada término del segundo. Es trabajo de hormiga, pero sistemático.

Para las fracciones algebraicas, aplica las mismas reglas que con fracciones numéricas. Puedes simplificar sacando factor común tanto en numerador como denominador.

¡Atención! Las fracciones algebraicas se simplifican igual que las numéricas: divide arriba y abajo por el mismo factor.

Recuerda que no puedes dividir por cero, así que siempre ten cuidado con los valores que pueden hacer cero el denominador. Estos valores se llaman "restricciones" del dominio.

Simplificación y Fracciones Algebraicas

Las fracciones algebraicas son como las fracciones normales, pero con letras. La clave está en factorizar numerador y denominador para encontrar términos comunes que puedas cancelar.

Para sumar fracciones algebraicas, necesitas encontrar el denominador común. Es exactamente igual que con fracciones numéricas: busca el mínimo común múltiplo de los denominadores.

La extracción de factor común es tu herramienta más poderosa. Siempre busca qué pueden compartir todos los términos: números, letras, o expresiones completas entre paréntesis.

¡Método infalible! Para simplificar fracciones algebraicas: 1) Factoriza numerador y denominador, 2) Cancela factores comunes, 3) Multiplica lo que quede.

Cuando tengas expresiones del tipo a$x+1$ + b$x+1$, puedes sacar $x+1$ como factor común y quedarte con $x+1$$a+b$. Es como encontrar el patrón oculto en la expresión.

Ejemplos Prácticos Resueltos

Vamos a ver ejemplos concretos para que todo cobre sentido. Con monomios semejantes, solo sumas o restas coeficientes: 3x + 2x = 5x, pero las partes literales deben ser idénticas.

Para multiplicar potencias de la misma base, sumas exponentes: x³ · x² = x⁵. Para dividir, restas exponentes: x⁷ ÷ x⁴ = x³.

Cuando multipliques un monomio por un polinomio, distribuye el monomio a cada término: 5x$x² + x - 2$ = 5x³ + 5x² - 10x.

¡Práctica perfecta! La multiplicación de polinomios requiere paciencia: cada término del primero por cada término del segundo, sin olvidar ninguno.

El producto $3x + 1$$5x + 2$ se resuelve así: 3x(5x) + 3x(2) + 1(5x) + 1(2) = 15x² + 6x + 5x + 2 = 15x² + 11x + 2. ¡Sistemático y sin prisa!

Casos Especiales y Productos Notables Avanzados

Los productos notables con radicales siguen las mismas reglas, solo que con más cuidado en los cálculos. $x + √27$² = x² + 2√27x + 27.

Para casos con fracciones dentro de radicales, como $[\sqrt{\frac{x}{3}}]²$, recuerda que el cuadrado elimina la raíz: queda x/3.

La factorización por agrupación es útil cuando tienes cuatro o más términos. Agrupa de dos en dos y busca factores comunes en cada grupo.

¡Estrategia inteligente! Si tienes ab² - a²b, saca primero ab: ab$b - a$. Siempre busca el factor común más grande posible.

Expresiones como 3x² + 6x² - 18x se pueden factorizar como 3x$x² + 2x - 6$. Primero saca el factor común numérico y literal, luego trabaja con lo que queda en el paréntesis.

Simplificación de Fracciones Algebraicas

La simplificación de fracciones algebraicas es como limpiar una ecuación: quitas lo innecesario para que quede más clara. La clave está en factorizar correctamente.

Para $\frac{4x + 4}{8}$, saca factor común del numerador: $\frac{4(x + 1)}{8} = \frac{x + 1}{2}$. Siempre busca factores comunes entre numerador y denominador.

Casos como $\frac{x + 3}{2x + 6}$ se simplifican factorizando el denominador: $\frac{x + 3}{2(x + 3)} = \frac{1}{2}$. El factor $x + 3$ se cancela arriba y abajo.

¡Técnica profesional! Antes de simplificar, factoriza completamente numerador y denominador. Solo entonces cancela factores idénticos.

Con expresiones cuadráticas como $\frac{x² + 2x + 1}{x² - 1}$, reconoce productos notables: $\frac{(x + 1)²}{(x + 1)(x - 1)} = \frac{x + 1}{x - 1}$. Los patrones te ahorran mucho trabajo.

Aplicaciones y Casos Complejos

Los casos más complejos requieren paciencia y método. Para $\frac{15x³ - 5x²}{30x² - 10x}$, saca factores comunes en numerador y denominador por separado.

Numerador: 15x³ - 5x² = 5x²$3x - 1$. Denominador: 30x² - 10x = 10x$3x - 1$. Resultado: $\frac{5x²(3x - 1)}{10x(3x - 1)} = \frac{5x²}{10x} = \frac{x}{2}$.

Las fracciones con términos repetidos se simplifican fácilmente: $\frac{3x - 5}{18x - 30} = \frac{3x - 5}{6(3x - 5)} = \frac{1}{6}$.

¡Método maestro! Siempre verifica tu respuesta sustituyendo valores. Si das el mismo resultado antes y después de simplificar, vas bien.

Para expresiones como $\frac{6x²}{3x² - 3x}$, factoriza el denominador: $\frac{6x²}{3x(x - 1)} = \frac{2x}{x - 1}$. La práctica hace que estos patrones se vuelvan automáticos.