Continuidad de Funciones

Una función es continua en un punto cuando no tiene "saltos" ni "huecos" en ese lugar. Para que f sea continua en x = a, necesitas que se cumplan tres condiciones súper importantes: que la función esté definida en ese punto, que exista el límite, y que el límite coincida con el valor de la función.

Los tipos de discontinuidad son fáciles de recordar si los visualizas. La discontinuidad evitable es como un "hueco" que podrías "tapar", mientras que la de salto finito es como un "escalón" en la gráfica. La de salto infinito es cuando la función se va hacia infinito.

Para funciones definidas a trozos, el truco está en revisar los puntos donde cambian las expresiones. Ahí es donde pueden aparecer discontinuidades, así que siempre comprueba esos "puntos de empalme" calculando los límites laterales.

💡 Consejo clave: Las funciones polinómicas, trigonométricas y exponenciales son siempre continuas en su dominio. ¡Una menos de la que preocuparse!

Ejercicios de Continuidad

Los ejercicios con funciones racionales son tu oportunidad de brillar. Recuerda que el denominador no puede ser cero, así que encuentra dónde se anula y estudia qué pasa en esos puntos críticos.

Para las funciones a trozos, tu estrategia es clara: primero estudia cada trozo por separado, luego enfócate en los puntos donde se "unen" las diferentes expresiones. Ahí es donde está la clave del ejercicio.

Cuando te pidan calcular valores de parámetros k, simplemente iguala los límites laterales. Es como resolver una ecuación normal, pero usando límites. Si los límites laterales son iguales, la función será continua en ese punto.

Los ejercicios de múltiples parámetros pueden parecer intimidantes, pero siguen la misma lógica. Planteas las ecuaciones de continuidad para cada punto conflictivo y resuelves el sistema resultante.

🎯 Truco de experto: Siempre representa gráficamente las funciones a trozos. Te ayudará a visualizar dónde pueden estar los problemas de continuidad.

Más Ejercicios de Continuidad

Los ejercicios con parámetros complejos requieren paciencia y método. Cuando tengas funciones como f(x) con parámetro 'a', estudia qué valores hacen que la función sea continua y cuáles la rompen.

Para funciones exponenciales y logarítmicas con parámetros, recuerda sus propiedades básicas. e^0 = 1 siempre, y ln(1) = 0. Estos valores te servirán como puntos de referencia en tus cálculos.

Los ejercicios de representación gráfica combinados con continuidad son especialmente útiles para exámenes. Te permiten visualizar el comportamiento de la función y entender mejor los límites en infinito.

Practicar con múltiples puntos de empalme te preparará para problemas más complejos. Cada punto de conexión entre trozos es una oportunidad de aplicar las condiciones de continuidad.

📝 Nota importante: Siempre verifica tus respuestas sustituyendo los valores encontrados en la función original.

Introducción a la Derivabilidad

La tasa de variación media es como calcular la velocidad promedio en un viaje. Te dice cuánto cambia la función entre dos puntos, pero no qué pasa en el camino.

La derivada es mucho más poderosa: te da la variación instantánea en cada punto. Es como saber tu velocidad exacta en cada momento del viaje, no solo el promedio. La fórmula con límites puede parecer complicada, pero es solo una manera formal de calcular la pendiente de la recta tangente.

Las derivadas laterales aparecen en puntos "problemáticos" donde la función cambia bruscamente de dirección. Si las derivadas por izquierda y derecha son diferentes, tienes un punto anguloso (como una esquina) y la función no es derivable ahí.

La relación entre derivabilidad y continuidad es clave: si una función es derivable, automáticamente es continua. Pero cuidado, el recíproco no siempre se cumple.

⚡ Concepto clave: Una función puede ser continua pero no derivable $piensa en |x| en x=0$, pero nunca puede ser derivable sin ser continua.

Reglas de Derivación

Las reglas básicas de derivación son tu caja de herramientas matemática. La derivada de una suma es la suma de las derivadas, y la derivada de una constante por función es la constante por la derivada de la función.

La regla del producto y del cociente requieren más cuidado. Para el producto: (fg)' = f'g + fg'. Para el cociente: $f/g$' = $f'g - fg'$/g². Un truco nemotécnico: "primero por segundo menos segundo por primero, todo entre segundo al cuadrado".

La regla de la cadena es fundamental para funciones compuestas. Si tienes f(g(x)), su derivada es f'(g(x)) · g'(x). Es como "pelar una cebolla": derivas capa por capa desde fuera hacia dentro.

Las derivadas básicas (potencias, trigonométricas, exponenciales, logarítmicas) debes memorizarlas. Son como el alfabeto de las matemáticas: las necesitarás constantemente.

🔧 Herramienta práctica: Practica las reglas con funciones sencillas antes de intentar ejercicios complejos. La velocidad vendrá con la práctica.

Relación entre Derivabilidad y Continuidad

Si una función es derivable en un punto, automáticamente es continua en ese punto. Esta es una relación unidireccional súper importante para entender el comportamiento de las funciones.

Para funciones simples (polinómicas, trigonométricas, exponenciales), el estudio de derivabilidad se reduce a calcular su dominio. Son derivables donde están definidas, lo que te ahorra mucho trabajo.

Las funciones a trozos requieren un análisis más detallado. Primero estudias la continuidad, luego calculas las derivadas de cada trozo, y finalmente comparas las derivadas laterales en los puntos de empalme.

El proceso es sistemático: continuidad → derivadas por separado → derivadas laterales en puntos críticos. Si las derivadas laterales coinciden, la función es derivable en ese punto.

📊 Método ordenado: Siempre sigue el mismo proceso: 1) continuidad, 2) derivadas por trozos, 3) derivadas laterales en empalmes.

Ejercicios de Derivabilidad

Los ejercicios de derivabilidad en puntos específicos te enseñan a aplicar la definición paso a paso. Calcula las derivadas laterales y compáralas: si son iguales, hay derivabilidad.

Las funciones con valor absoluto son clásicas en exámenes. Recuerda que |x| cambia su expresión en x=0, así que ahí debes estudiar derivabilidad. En general, busca dónde la expresión dentro del valor absoluto se hace cero.

Los ejercicios con parámetros combinan derivabilidad con resolución de sistemas. Planteas las condiciones de continuidad y derivabilidad, y obtienes ecuaciones que te permiten hallar los parámetros.

Para funciones exponenciales y logarítmicas en trozos, ten cuidado con los dominios. ln(x) solo existe para x>0, y esto puede afectar la derivabilidad en los puntos límite.

🎯 Estrategia ganadora: En funciones a trozos, identifica primero los puntos "sospechosos" (donde cambian las expresiones) y concéntrate en estudiarlos.

Aplicaciones de las Derivadas: Tangentes y Monotonía

La ecuación de la recta tangente es una aplicación directa de la derivada. Si tienes f'(a), esa es la pendiente de la tangente en x=a. La ecuación queda: y - f(a) = f'(a)$x - a$.

Para hallar tangentes paralelas a rectas dadas, iguala la derivada a la pendiente de esa recta. Resuelve f'(x) = m y obtienes los puntos donde esto ocurre.

La monotonía (crecimiento y decrecimiento) se lee directamente de la derivada. Si f'(x) > 0, la función crece; si f'(x) < 0, decrece. Los puntos donde f'(x) = 0 son candidatos a extremos.

Para estudiar monotonía, halla f'(x) = 0, encuentra los intervalos que estos puntos determinan, y estudia el signo de f' en cada intervalo.

📈 Visualización clave: La derivada positiva significa que la función sube (pendiente positiva), la negativa que baja. ¡Es así de simple!

Extremos Absolutos y Relativos

Los extremos relativos son "picos" y "valles" locales en tu función. Un máximo relativo es el punto más alto en su "vecindario", aunque puede haber puntos más altos en otras partes de la función.

Los extremos absolutos son los valores más grandes y más pequeños de toda la función en el intervalo que estudies. Son únicos (si existen), mientras que puede haber varios extremos relativos.

Para encontrar extremos en intervalos cerrados, busca: puntos donde f'(x) = 0, puntos donde f no es derivable, y los extremos del intervalo. Calcula f en todos estos puntos y compara.

La interpretación gráfica es fundamental. Un máximo relativo es donde la función pasa de creciente a decreciente, y un mínimo donde pasa de decreciente a creciente.

🏔️ Analogía útil: Piensa en el perfil de una montaña: los extremos relativos son picos y valles locales, los absolutos son la cumbre más alta y el valle más profundo de toda la cordillera.

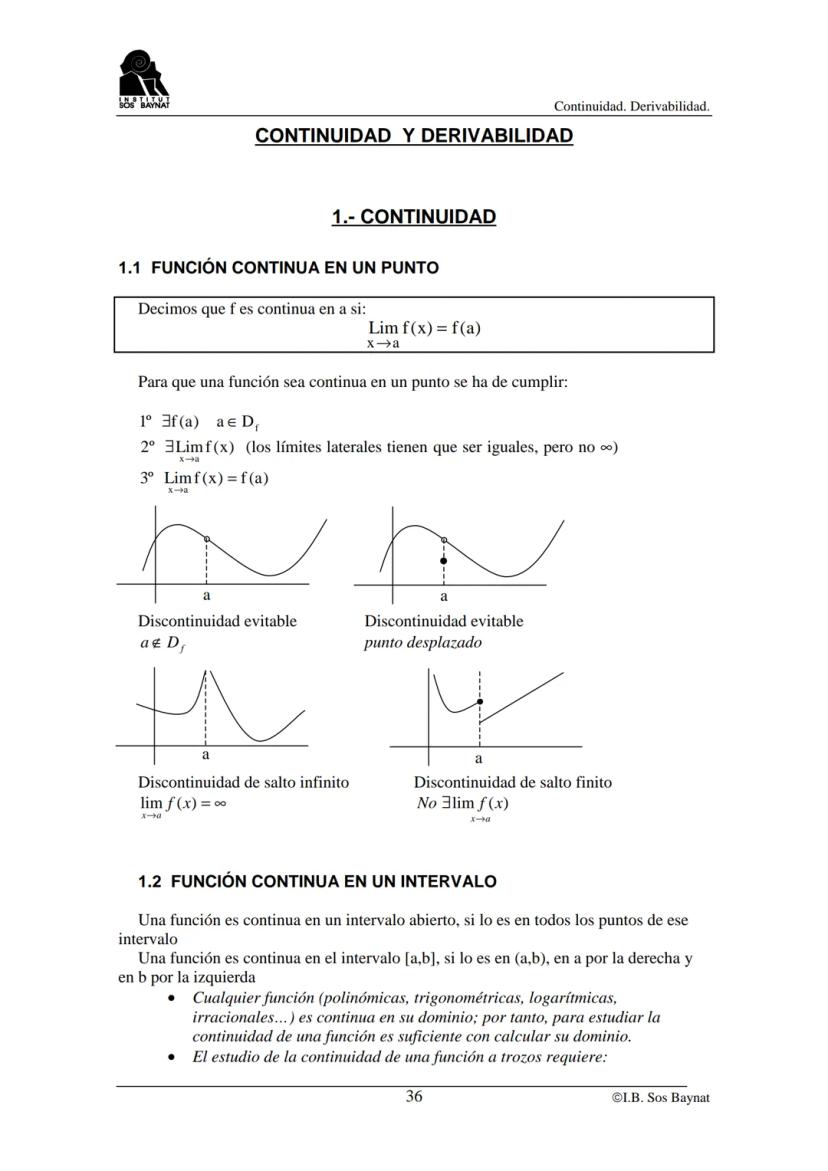
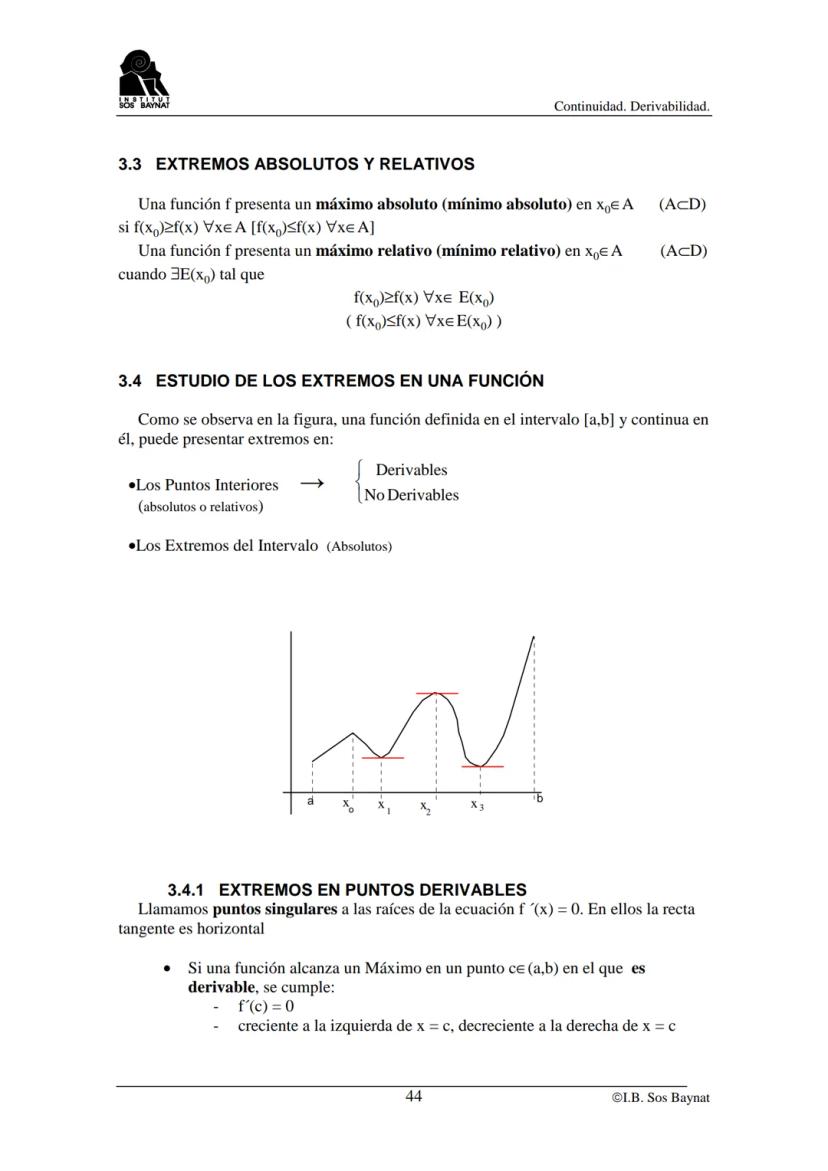
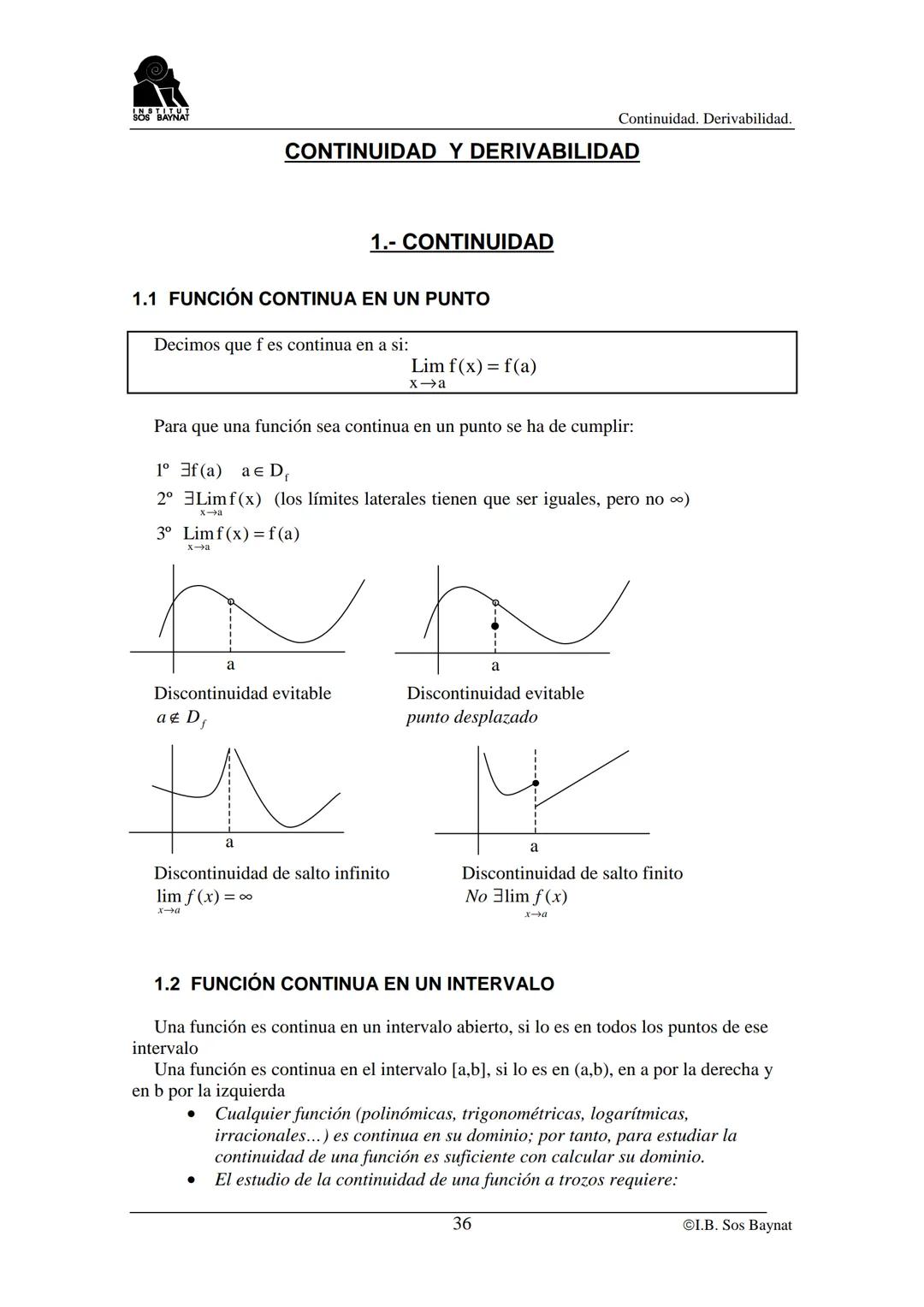
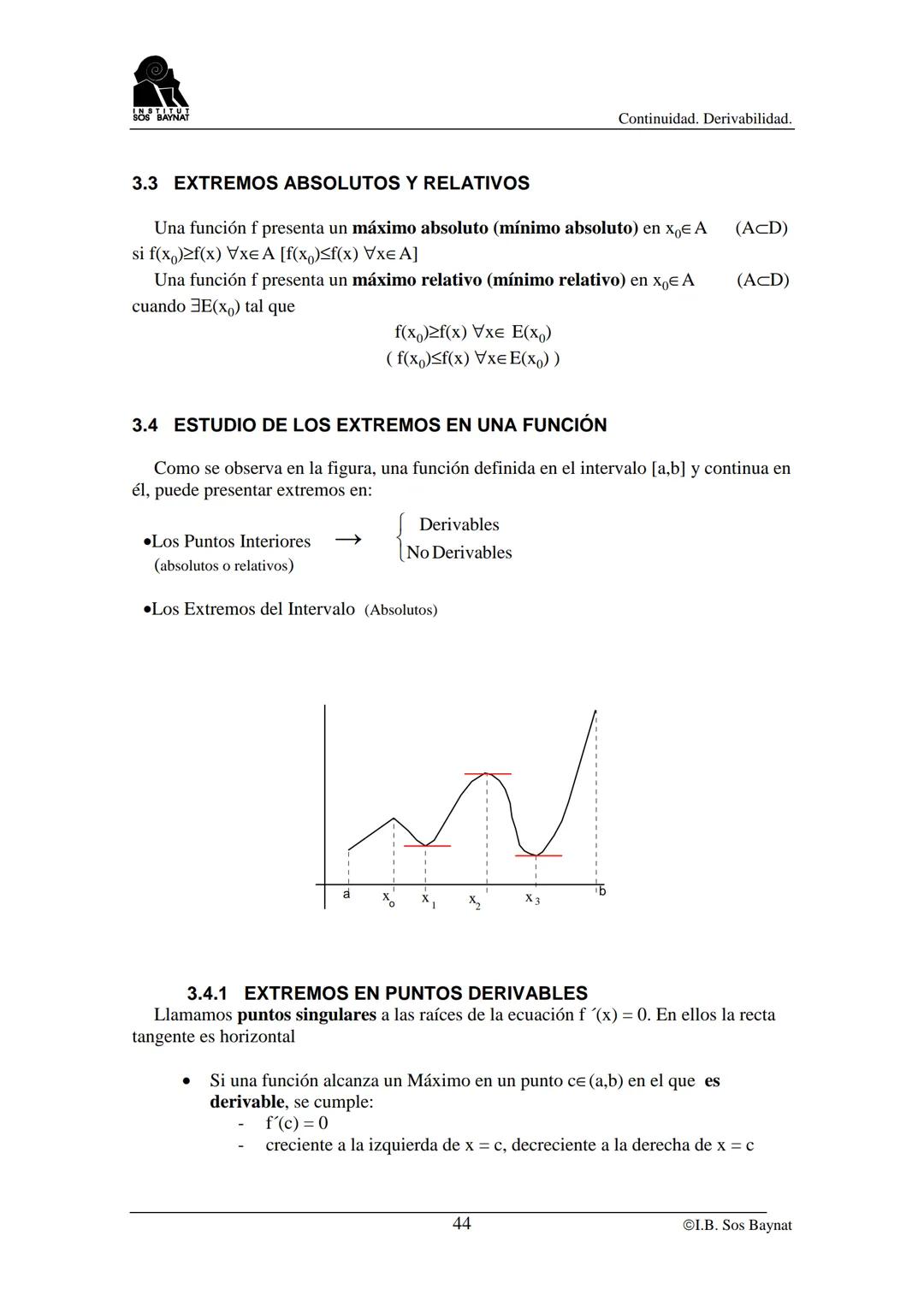
Cálculo de Extremos Absolutos

Para hallar extremos absolutos en [a,b], necesitas ser sistemático: encuentra los extremos relativos en (a,b), evalúa f(a) y f(b), y compara todos los valores obtenidos.

Los criterios de extremos son tu guía. En un máximo: f'(x) = 0 y la función pasa de creciente a decreciente. En un mínimo: f'(x) = 0 y pasa de decreciente a creciente.

Los ejercicios de optimización con parámetros combinan varias técnicas. Usa las condiciones dadas (puntos por los que pasa, tangentes específicas) para formar un sistema de ecuaciones.

Las aplicaciones prácticas de extremos aparecen constantemente en problemas reales: maximizar beneficios, minimizar costos, encontrar dimensiones óptimas. La derivada es tu herramienta principal para resolverlos.

🎯 Método infalible: 1) Encuentra puntos críticos, 2) Evalúa en extremos del intervalo, 3) Compara todos los valores, 4) Identifica máximo y mínimo absolutos.